Криптосистему Эль-Гамаля используют для того, чтоб сформировать электронную подпись, или для шифровки данных. В данной статье рассмотрены идея этого метода шифрования, описание алгоритма.
Ключевые слова: криптосистема Эль-Гамаля, шифр, схема, шифрование, дешифрование, алгоритм, открытый ключ, закрытый ключ.
Криптосистема Эль-Гамаля — это шифрование с открытым ключом, которая базируется на свойствах дискретного логарифма. Непосредственное ее преимущество над алгоритмом RSA в том, что в RSA есть возможность подделать цифровую подпись под некоторыми сообщениями, без определения секретного ключа, когда в методе шифрования Эль-Гамаля такая возможность отсутствует.
Шифр Эль-Гамаля лежит в основе бывших стандартов электронной цифровой подписи в США (DSA) и России (ГОСТ Р 34.10–94).
Идея метода шифрования
Основная идея метода шифрования Эль-Гамаля заключается в том, что эффективного метода сравнивания ax==b (modp) не существует.
Обозначим через Z(n) вычеты по модулю n, через Z*(n)- мультипликативную группу обратимых элементов в Z(n), ab(modn) — возведение в степень b, принадлежащих Z(n).
Допустим, числа p и 2p+1 являются простыми, p>2, v — образующая мультипликативная группа Z*(p), а w — Z*(2p+1).
Лемма: если v — образующая Z*(p), то v0=(p+(p+1) v)(mod 2p) — образующая мультипликативная группа Z*(2p). А эта группа изоморфна Z*(p), поскольку если p является простым числом, то группа Z*(p) изоморфна Z(p-1).
Описание алгоритма
Для генерации пары ключей следует выбрать простое число p:
{ bool check = true;
if ((num % 10) % 2 == 0 && num!= 2)
{ TxtResult.Text = _mesNo;
return;}
BigInteger sqrtnum = Sqrt(num);
int del = 3;
while (del <= sqrtnum)
{ if (num % del == 0)
{ TxtResult.Text = _mesNo;
return;}
del += 2;}}
TxtResult.Text = _mesYes;
}static BigInteger Sqrt(BigInteger n)
{BigInteger x = n, y = n;
do{
y = x;
x = (y + (n / y)) / 2; }
while (y > x);
returnx; }
Листинг 1. Проверка на простое число p
Затем нужно выбрать два случайных числа g и x, которые строго меньше p: (g < p, x < p)
{ Random random = new Random();
k = random.Next(0, 10000);
if (GetNOD(k, p — 1) == 1)
{ g = random.Next(0, (int)p);
x = random.Next(0, (int)p);
break;}
Листинг 2. Задание двух случайных элементов q и x.
Далее нужно получить значение y из выражения: y = g xmodp.
ReturnValue ret = new ReturnValue();
num1 = BigInteger.Abs(num1);
num2 = BigInteger.Abs(num2);
BigInteger i = num2, x = 0, y = 1;
while (num1 > 0)
{ BigInteger q = i / num1, x1 = num1;
num1 = i % x1;
i = x1;
x1 = y;
y = x — q * x1;
x = x1;}
x %= num2;
if (x < 0) x = (x + num2) % num2;
ret.SetValue(x);
if (x!= 1)
{ ret.SetGetBoolValue(true);}
else
{ ret.SetGetBoolValue(false);}
returnret;
Листинг 3. Получение значения y.
Тройка чисел (y, g, p) является открытым ключом, причем g и p можно сделать общими для группы пользователей, х в свою очередь является закрытым ключом.
Для того, чтобы подписать сообщение M, вначале нужно выбирать случайное число k, так что бы НОД (k, p — 1) = 1
num1 = BigInteger.Abs(num1);
num2 = BigInteger.Abs(num2);
if (num1 * num2 == 0 {
return 1;}
while (num1!= num2)
{ if (num1 > num2)
{ num1 -= num2;}
else
{ num2 -= num1;}}
return num1;
Листинг 4. Выбор случайного значения k.
Значение k в дальнейшем сохраняется в секрете. Далее вычисляется значение a из выражения a = g kmodp.
Следом для нахождения b помощью расширенного метода Евклида решается уравнение: M = (xa + kb) mod (p — 1).
Подписью является пара чисел (a, b). Для того, чтоб убедиться в ее верности, необходимо проверить справедливость следующего равенства:
y a * ab mod p = g M mod p.
for (int i = 0; i < M.Length; i++)
{ if (((BigInteger.ModPow(y, a, p) * BigInteger.ModPow(a, b [i], p)) % p) == (BigInteger.ModPow(g, M [i], p)))
{ res.SetCheckValue(BigInteger.ModPow(g, M [i], p)); }
else
{ res.SetCheckValue(0);
break;}}
Листинг 5. Верно ли равенство.
Для каждой процедуры подписания необходимо новое значение k, которое выбирается случайным образом. Компрометация значения k дает возможность по перехваченным значениям M, a и b восстановить за полиномиальное время значение секретного ключа x.
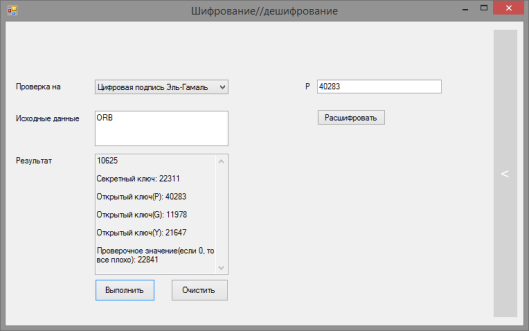
Рис. 1. Пример шифрования цифровой подписью Эль-Гамаля
Заключение
В качестве иллюстрации к статье можно привести пример шифрования методом Эль-Гамаля (Рисунок 1).
Следует добавить, алгоритм Эль-Гамаля является криптосистемой с открытым ключом, которые в настоящее время считаются наиболее эффективными.
Литература:
- С. Бабичев. Криптография без секретов. 2012
- С. Сингх. Книга шифров. Тайно истории шифров и их расшифровки. М.: Аст, Астрель, 2006. 447 с.
- Б. А. Фороузан. Схема цифровой подписи Эль-Гамаля. Управления ключами шифрования безопасности и безопасности сети.

