Данная статья посвящена проблеме реализации межпредметной связи математики и информатики при изучении математики в основной школе.

Ключевые слова: межпредметные связи, график.

В условиях обновления и развития системы общего и профессионального образования одной из главных ее целей является формирование научного мировоззрения, целостного представления о мире и месте человека в нём. Особую роль в этих условиях приобретает естественнонаучное образование, так как основу научного мировоззрения составляет естественнонаучная картина мира, которая является результатом интеграции знаний физики, химии и биологии, астрономии и других наук.

В связи с этим актуальной становится проблема содержательного и процессуального пересмотра естественнонаучного образования, в котором должны быть максимально реализованы межпредметные связи, что существенно облегчит изучение смежных дисциплин и, в конечном счете, целостное восприятие окружающего мира, его диалектическое единство и эволюцию.

Проанализировав учебную литературу Н. В. Макаровой можно сделать вывод, что автор в процессе изложения материала по информатике чаще всего прибегает к односторонним содержательным межпредметным связям.

Проанализировав учебную литературу И. Г. Семакина можно сделать вывод, что автор в процессе изложения материала по информатике в равной степени прибегает как к односторонним содержательным, так и к односторонним операционным межпредметным связям.

Проанализировав учебную литературу Угриновича Н. Д., можно сделать вывод, что автор в процессе изложения материала по информатике чаще всего прибегает к односторонним содержательным межпредметным связям.

Сравнивая учебники различных авторов, мы пришли к выводу, что наиболее часто употребляются односторонние содержательные межпредметные связи. Следовательно, именно они являются предпосылкой для эффективного изучения информатики. На наш взгляд учебно-методический комплект под редакцией Макаровой Н. В. — это оптимальный выбор для реализации межпредметных связей информатики и математики в курсе информатики.

Анализ базовых учебников по информатике позволяет сделать вывод о том, что реализация межпредметных связей с математикой осуществляется в основном на уровне односторонних и содержательных связей. Практически отсутствуют многосторонние и методические связи, что позволяет сделать вывод о необходимости усиления межпредметных связей курсов информатики и математики в рамках специально разработанной методики. Так реализацию многосторонних и методических связей, выводящих на уровень теоретических связей предметов математики и информатики можно осуществить на интегрированных уроках и специально разработанных внеклассных занятиях.

Из анализа учебников по информатике и математике видно, что их содержание не всегда соответствует друг другу: присутствуют темы, изучаемые в информатике раньше, чем темы математики, на материал которых опирается их содержание. Следовательно, учителю информатики необходимо при разработке собственной программы проанализировать программу учителя математики и соответствующие ей учебники для построения логики изучения своего предмета с учетом межпредметных связей информатики и математики.

Остановимся более подробно на методике построения графиков функций, так как очевидна межпредметная связь с информатикой.

Существуют определенные методы построения графиков функций в математике. График функции — это множество точек, у которых абсциссы являются допустимыми значениями аргумента х, а ординаты — соответствующими значениями функции y.

Если буквально следовать определению, то для построения графика некоторой функции нужно найти все пары соответствующих значений аргумента и функции и построить все точки с этими координатами. В большинстве случаев это сделать практически невозможно, так как таких точек бесконечно много. Поэтому обычно исследуют функцию, что даёт возможность найти область определения и область изменения функции, области её убывания или возрастания, асимптоты, интервалы знакопостоянства и т. д.; находят несколько точек, принадлежащих графику, и соединяют их плавной кривой. Однако при построении графиков многих функций часто можно избежать проведение подобного исследования, используя ряд методов, упрощающих аналитическое выражение функции и облегчающих построение графика.

Для построения графика функции y=f(x)+b (где y=f(x) — простейшая функция, график которой нам известен) следует построить график функции y=f(x), причём горизонтальную ось начертить штриховой линией и затем сдвинуть её на b единиц вниз, если b>0 и на b единиц вверх, если b<0. Это и будет истинная ось х-ов; полученный в новой системе координат график является графиком функции y=f(x)+b.

Большой интерес у учащихся вызывают обобщающие уроки математика — информатика («Графический способ решения систем уравнений в среде Microsoft.Excel, Open.Calc» 9 класс, «Решение неравенств с одной переменной» 8 класс, «Решение уравнений» 9 класс, «Решение квадратных уравнений» 8 класс, «Графики функций и их свойства» 9 класс, «Циклические алгоритмы. Построение графиков тригонометрических функций» 10 класс). Такие уроки используются в тех случаях, когда знание материала одних предметов необходимо для понимания сущности процесса, явления при изучении другого предмета.

На уроках математики в 7 классе можно использовать следующие задания.

Задание 1.

В одной системе координат построить графики функций.

у= 2х у=4x

y=-3x

y=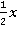 y=x

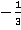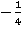y=x

Глядя на график, сделать вывод о зависимости положения графика функции прямой пропорциональности от коэффициента /k/.

Вывод:1) если k>0, то график находится в I и III координатных четвертях, если k<0, то во II и IV

2)если /k/>1, то график приближается к оси OY.

/k/<1, то график приближается к оси OX.

Задание 2.

В одной системе координат построить графики функций.

y= 2x

y=2x+3

y=2x-2

Сделать вывод о взаимном положении графиков линейной функции на плоскости и выдвинуть гипотезу, почему это может быть? Как проверить эту гипотезу?

Вывод: графики параллельны, у них одинаковый коэффициент k=2.Построить еще один график с тем же коэффициентом y=2x-4,5.Проверить гипотезу.

Рассмотрим примеры заданий для 9-го класса.

Задание 1. Построить в одной и той же системе координат графики функций:

y=x²

y= x²+3 y=(x-5)² y=(x-3)²+1

y= x^2–4 y=(x+3)²

и сделать вывод о соответствующих преобразованиях графиков функций.

Вывод: 1) если k функции +b, то ­

—b, то ¯

Если k аргументу +а, то ¬

—а, то ®

Задание 2. Иллюстрация графического способа решения уравнений

x³+x-4=0

x³=-x+4

Построить в одной системе координат графики функций

y= x³ y=-x+4 найдем точку пересечения. Ее абсцисса –корень уравнения.

Задание 3. Графический способ решения систем уравнения

1)

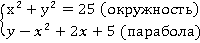
(4 решения)

2) 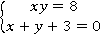 Û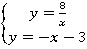

3)

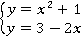
Рассмотрим более подробно, как с помощью Open.Calc решить последнюю систему уравнений.

Для графической визуализации данных в электронных таблицах используются диаграммы (круговые, линейчатые и т. д.). Диаграммы наглядно отображают зависимость между данными, что облегчает их восприятие и помогает при анализе и сравнении данных.

Для построения диаграммы необходимо выполнить следующие шаги:

1.      Выделить диапазон ячеек, содержащих необходимые данные (если данные находятся в несмежных ячейках, то их выделяют, удерживая нажатой клавишу Ctrl).

2.      Запустить Мастер диаграмм с помощью команды Вставка → Диаграмма.

3.      Выбрать тип диаграммы.

4.      Уточнить детали отображения диаграммы, ввести заголовок и др.

5.      Нажать кнопку Готово. При необходимости изменить формат подписей данных, цвет заливки областей диаграммы и т. п. (используя для этого команду Свойства объекта контекстного меню).

6.      Щелкнуть мышкой вне области окна диаграммы и при необходимости изменить

Интеграция в обучении позволяет выполнить и развивающую функцию, необходимую для всестороннего и целостного развития личности учащегося, развития интересов, мотивов, потребностей к познанию.

Использование межпредметных связей в обобщающем повторении играет большую положительную роль не только в повторении и закреплении определенных тем и разделов, но и в усвоении важнейших обобщающих понятий, встречающихся в разных предметах, и может осуществляться в таких формах, как олимпиады, открытые занятия, тесты, деловые игры и т. д.

Литература:

1.                  Бакирова А. Ю. Дифференцированное обучении (методические рекомендации), ТГПУ, 2009.

2.                  Бакирова А. Ю. Методика преподавания математики. Учебное пособие. — Т., 2010.

3.                  Волошенко Л. Н. Межпредметные связи на уроках информатики//По материалам семинара, 2009.

4.                  Гриншкун В. В., Левченко И. В. Школьная информатика в контексте фундаментализации образования. — М.: Московский городской педагогический университет, 2008. — С.131–136

5.                  Гурьев А. И. Методологические основы построения и реализации дидактической системы межпредметных связей в курсе физики средней школы: дис. д-ра пед. наук. [Текст]/А. И. Гурьев, Челябинск, 2008. — 372с.

6.                  Кузнецова Л. Г. Реализация межпредметных связей в учебниках математики для непрофильных специальностей / Л. Г. Кузнецова// Вестник Тамбовского государственного университета. — 2009. — Выпуск 3. — С. 72–80.

7.                  Левченко И. В., Карташова Л. И. Задачи межпредметного характера как средство развития познавательной мотивации старшеклассников на уроках информатики // Информационные технологии в науке и образовании: Сборник научных трудов. — Воронеж: Научная книга, 2009. — С.68–73.