Рассматривается математическая модель двухфазной фильтрации. Построены разностные схемы дифференциальных уравнений и начальных и граничных условий, соответствующих этим дифференциальным уравнениям. Результаты полученные при реализации выбранной модели, описывающей вытеснение нефти водой, хорошо согласуются с результатами изученных работ.
Ключевые слова: математическое моделирование, численные методы, двухфазная фильтрация, давление, насыщенность, пористость, несжимаемая жидкость.
Введение
Движение природных жидкостей (нефти, газа и подземных вод) через поры и трещины горных пород называется фильтрацией. Это движение может быть следствием как естественных процессов, так и вмешательства человека, связанного с процессом нефтегазодобычи [2].
Большинство уникальных и крупных месторождений в нефтяных регионах России находятся в поздней и конечной стадиях разработки. При современных методах разработки месторождений 50 % и более первоначальных природных запасов нефти остаются неизвлекаемыми [6]. Поэтому одной из главных задач является увеличение коэффициента нефтеотдачи.
Математическая модель
Рассмотрим двумерную математическую модель двухфазной фильтрации. Для простоты будем пренебрегать действием капиллярных и гравитационных сил. Жидкости и пористая среда считаются несжимаемыми.
В данном случае, исходная система, состоящая из гиперболического уравнения для насыщенности и эллиптического уравнения выглядит следующим образом:
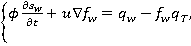 (1)
(1)
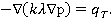 (2)
(2)
где 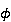 — пористость среды,
— пористость среды, 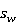 — водонасыщенность,
— водонасыщенность, 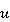 — суммарная скорость фильтрации воды и нефти,
— суммарная скорость фильтрации воды и нефти, 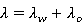 — общая подвижность,
— общая подвижность, 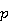 — давление в пласте,
— давление в пласте, 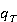 — сумма объемных источников и стоков.
— сумма объемных источников и стоков.
Начальные и граничные условия записываются в виде
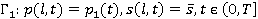 (3)
(3)
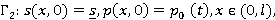 (4)
(4)
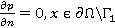
 (5)
(5)
Рассмотрим два случая, когда 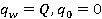 и
и 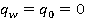 .
.
Аппроксимация по пространству и времени
Определим пару функций 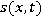 и
и 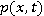 из условий (1)-(5). Проведем аппроксимацию уравнений на равномерной прямоугольной сетке для случая явной аппроксимации по времени:
из условий (1)-(5). Проведем аппроксимацию уравнений на равномерной прямоугольной сетке для случая явной аппроксимации по времени:
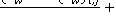
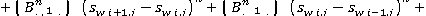
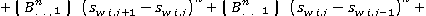
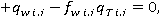 (6)
(6)
Где
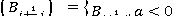 (7)
(7)
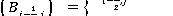 (8)
(8)
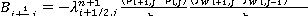 (9)
(9)
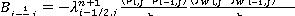 (10)
(10)
Аналогично, запишем конечно-разностную аппроксимацию для уравнения суммарной скорости:
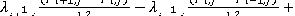
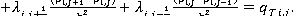 (11)
(11)
Результаты расчетов
При расчетах использовались следующие входные параметры модели: 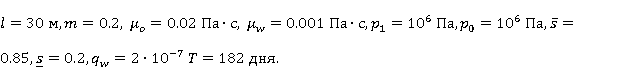
Относительные фазовые проницаемости заданы следующим образом:
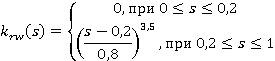
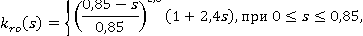
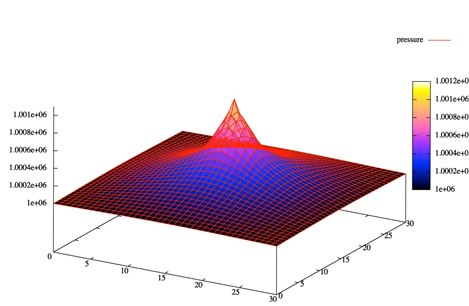
Рис. 1. Распределение давления
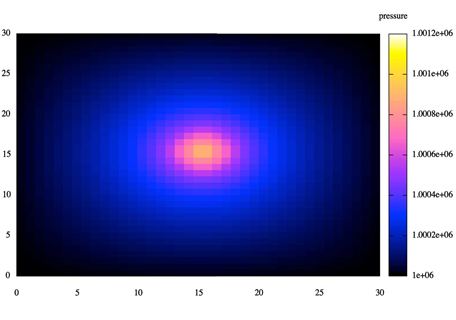
Рис. 2. Распределение давления
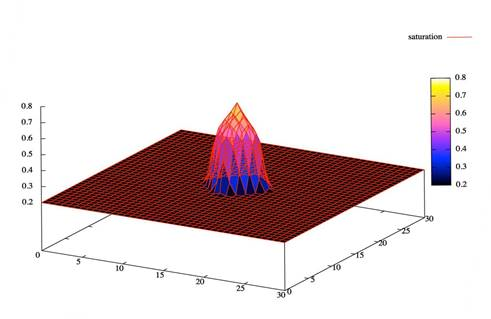
Рис.3. Распределение насыщенности
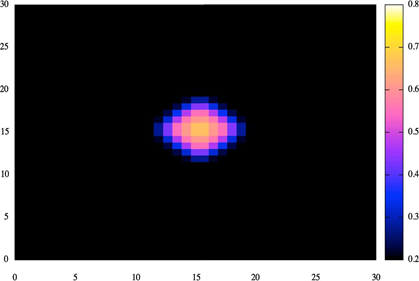
Рис. 4. Распределение насыщенности
Аппроксимация системы уравнений производилась по явным разностным схемам, вычислительный алгоритм реализован на языке С, необходимые расчеты производились при помощи вычислительной библиотеки GSL, графическая визуализация сделана в программе gnuplot.
Результаты, полученные при реализации выбранной модели, описывающей вытеснение нефти водой, хорошо согласуются с результатами изученных работ.
Литература:
1. Афанасьева Н. М., Васильева М. В., Колесов А. Е. Математическое моделирование фильтрации: учебное пособие. — Якутск: Издательско-полиграфический комплекс СВФУ, 2011, 86 с.;
2. Басниев К. С., Дмитириев Н. М., Каневская Р. Д., Максимов В. М. Подземная гидромеханика. М., Ижевск: Ин-т компьют. исследований, 2006. 488 с.
3. Васильев В. И., Попов В. В., Тимофеева Т. С. Вычислительные методы в разработке месторождений нефти и газа — Новосибирск: Издательство СО РАН, 2000, 126 с.
4. Мыхтарянц С. А., Чудов Л. А., Чурмаев О. М. Численные методы решения одномерной задачи о вытеснении нефти водой. В сб.: Численные методы решения задач фильтрации несжимаемой жидкости. — Новосибирск: ВЦ СО АН СССР, 1975, с. 242–249;
5. Самарский А. А. Теория разностных схем. М., 1977;
6. Щелкачев В. Н. Сравнительный анализ нефтедобычи и разработки нефтяных месторождений по странам мира. — М.: ВНИИОЭНГ, 1996. — 120с.

