Системный подход проектирования композиционного материала, как системы, предполагает построение обобщенной математической модели, состоящей из совокупности частных моделей, описывающих каждое из свойств в отдельности. Поэтому для упрощения обобщенной модели целесообразно сократить количество существенных свойств. Для этого можно оценить корреляционную связь между отдельными свойствами композитов. Если эта связь существенна, то с определенной точностью моделирования при синтезе одно из свойств можно исключить из технического задания. Так, было установлено, что имеется существенная связь между пределом прочности при сжатии и твёрдостью для эпоксидных композитов. А именно, по указанным в таблице 1 рангам прочности при сжатии и твёрдости эпоксидных композитов был определен коэффициент ранговой корреляции Спирмена.

Таблица 1

Здесь объединённые ранги отсутствуют и

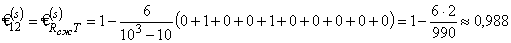
(можно показать, что R_сж= 20 T — 2,3).

Как видим, при проектировании рассматриваемых композитов возникает принципиальная возможность исключить экспериментальное определение одного из рассмотренных показателей.

Исследовалась также связь между коэффициентом структуры и коэффициентом энергоёмкости ЭК (табл.2).

Таблица 2

Оказалось, коэффициенты структуры и энергоёмкости должны определяться по экспериментальным данным самостоятельно:

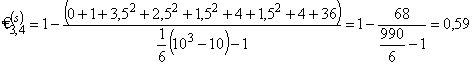
(при ранжировке по признаку x₁₃имеется одна группа с неразличимыми рангами 5,5; число элементов в группе m₃ = 1; 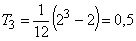; для x₄имеем T₄= 0,5).

Теснота связи между ранжировками X_k, X_j определяется коэффициентом корреляции Спирмена

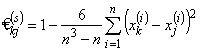
(пригодна лишь в случае отсутствия объединённых рангов в ранжировках X_k, X_j). При совпадающих ранжировках (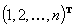, 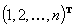; 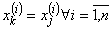) имеем 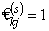; при противоположных ранжировках (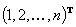, 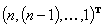;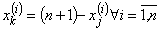) справедливо .

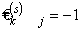При ранжировке по признаку x_k имеется m_k групп с неразличимыми рангами, и пусть далее n_q^k — число элементов в q-й группе, 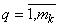. Для ранжировки по признаку x_k используется величина 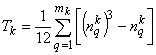. Если q-я группа состоит лишь из одного элемента (n_q^k = 1), то  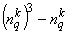= 0, и эти элементы в расчёте величины T_k фактически не участвуют. При отсутствии объединённых рангов при ранжировке по признаку x_k (m_k = n; n₁^k = n₂^k =... = n_n^k = 1) справедливо T_k = 0.

В общем случае анализ парных ранговых статистических связей производится по ранговому коэффициенту корреляции Спирмена

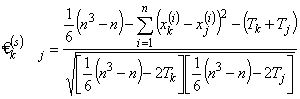
(если T_k иT_j малы по сравнению с 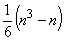, то приближённо можно принять:

;

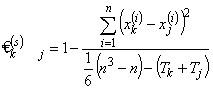формула точна при T_k = T_j).

При анализе парных ранговых статистических связей между ранжировками часто пользуются ранговым коэффициентом корреляции Кендалла (связаны между собой; коэффициенты — линейные функции от числа инверсий в перестановке); если абсолютные величины их значений не слишком близки к 1 и n ³ 10, то 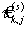 » 1,5 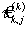. Напомним, что в некоторой перестановке числа i и j составляют инверсию, если i > j, но i стоит в этой перестановке раньше j. Для двух ранжировок X_k и X_j (соответствуют две перестановки x_k⁽¹⁾, x_k⁽²⁾,..., x_k⁽ⁿ⁾и x_j⁽¹⁾,x_j⁽²⁾,..., x_j⁽ⁿ⁾) естественной мерой нарушения порядка символов в одной перестановке от другой будет число s расположенных в неодинаковом порядке пар элементов (при X_k = (1, 2,..., n) указанная мера совпадает с числом инверсий в перестановке x_j⁽¹⁾,x_j⁽²⁾,..., x_j⁽ⁿ⁾ и определяет минимальное число s транспозиций в этой перестановке, необходимых для приведения её к виду 1, 2,..., n).

Известно, при указанных выше условиях 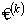 распределяется нормально со средним значением 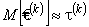и с дисперсией 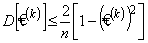; пространство элементарных исходов 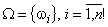, состоит из N = n! всевозможных перестановок и не зависит от x_k. Поскольку множество элементарных исходов W дискретно и конечно, то любое его подмножество измеримо и, следовательно, может интерпретироваться как случайное событие. При определении коэффициентов Спирмена и Кендалла речь, таким образом, идет о выборочных характеристиках ранговой связи. Возникает вопрос, как точно выборочные характеристики, определённые по указанным выше формулам, оценивают истинные теоретические значения. Теоретическими значениями коэффициентов 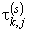,  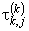являются значения, вычисленные по приведенным формулам с заменой объёма выборки n объёмом N генеральной совокупности.

Доверительный интервал нормально-распределённой случайной величины 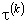 с дисперсией  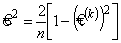есть интервал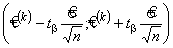; t_b определяется из условия b = 2 Ф(t_b),  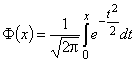(t_b = 1,96 при b = 0,95).

При заданном уровне значимости a следует признать наличие статистически значимой ранговой корреляционной связи, если 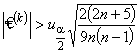 и n > 10;

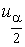 — 100 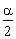 % -ная точка стандартного нормального распределения .

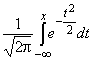При использовании коэффициента Спирмена проверка значимости осуществляется по неравенству

,

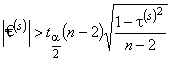где 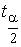 — 100 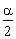 % -ная точка распределения Стьюдента.

При данных таблицы 1 дисперсия 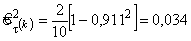, а доверительный интервал — 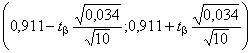. При b = 0,95; t_b = 1,96 получим интервал — (0,797; 1,025); с учетом — 1 <  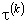< 1 искомый доверительный интервал есть (0,797; 1).

Предлагаемая методика многократно использовалась при многокритериальном синтезе сверхтяжелых и химически стойких композиционных материалов специального назначения [1…3] и подтвердилась ее эффективность.

Литература:

1.                  Будылина Е. А., Гарькина И. А., Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. –2013. — № 2 (16). — С. 138–142.

2.                  Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / Молодой ученый. –2013. — № 5. — С. 42–45.

3.                  Гарькина И. А., Данилов А. М., Жегера К. В. Математическое программирование в управлении качеством материалов / Региональная архитектура и строительство. –2014. –№ 1. — С. 30–36.