Рассмотрен процесс разборки сложной продукции, произведено математическое описание согласно модели, разрабатываемой автором. Представлены алгоритмы монтажа-демонтажа изделия с учетом доступности его компонентов.
Ключевые слова:математическое моделирование, граф, алгоритм, состав, структура, сложная продукция, доступность, производственный процесс.
1. Введение
Современная конкурентная бизнес-среда заставляет компании производить новые продукты как можно более эффективно.
Одними из основных ключевых моментов, определяющих вопрос общей эффективности производства, являются процессы разработки продукта [2].
Явной пользой для производства является возможность производить больше продукции с таким же количеством затраченных ресурсов, как и раньше. Чем больше эффективность процесса, тем больше продукции можно произвести при ограниченных ресурсах.
Это, как правило, достигается, когда в процессе разработки изделия, как проектной, так и практической, устраняются «узкие места». В настоящее время на производстве для решения этой задачи широко распространен модульный подход при проектировании и создании изделия. Также принцип модульности захватывает новые области промышленности, что подтверждают последние тенденции на рынках телекоммуникаций, микроконтроллеров и автопромышленности.
Новые области — это новые объекты автоматизации, открывающие простор для новых подходов при моделировании и организации единого информационного пространства, что в свою очередь является неоспоримым подтверждением актуальности рассматриваемой задачи.
Принципы модульного производства и проектирования, а также адаптивного производственного процесса, требуют гибкой и универсальной математической модели составного модульного (сложного) изделия. Математическая модель должен адекватно описывать состав и структуру, и позволять на её основе создавать удобные программные продукты для интеграции в единое информационное пространство предприятия [3].
2. Математическое моделирование сложной продукции и оценка адекватности полученных моделей
2.1. Введение понятий состава и структуры
В предыдущих статьях из этого цикла была предложена математическая модель, в основе которой лежит понятие состава продукта:
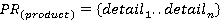
где i = 1.. n — определяет сколько тех или иных типов деталей в продукте;
detaili — коэффициент входимости для детали i.
Т. е. под продуктом понимается композиция деталей. Также предлагаемая модель учитывает, что детали могут быть заменяемы «кроссами», а само изделие может выступать как деталь более сложного продукта или иметь несколько версий-вариантов исполнения [1]. Другими словами, в рамках предложенной модели производится формализованное описание связей между установленным набором компонентов в контексте конструкторского замысла или проекта. А иллюстрирование самих отношений производится в виде графов. Например, основываясь на предлагаемой модели мы можем построить граф для определения доступности порядка процессов монтажа-демонтажа составных компонентов-деталей продукта.
В данной же статье, мы проанализируем адекватность предлагаемой модели структуры и компонентов продукта.
2.2. Описание процессов сборки/разборки
Для рассмотрения на практическом примере процессов сборки и разборки в рамках эксперимента возьмем виртуальный прибор, состоящий из десяти основных компонентов. В условиях реального производства это может быть любое типовое изделие.
Для иллюстрирования процесса и создания руководств рекомендуется использовать CAD систему Solid Works. Таким образом, на основе математической модели с использованием CAD систем можно генерировать руководства по сборке и разборке. Это не только позволит максимально быстро пополнить информационное обеспечение, но и повысит его доступность. Также можно дополнять уже имеющуюся базу альтернативными сценариями сборки и разборки изделия, и что не маловажно — создавать мульти-язычную базу, что в свою очередь особенно актуально для распределённых производств.
В данном примере отражена группировка — с компонентами «Деталь 3» будет связано единственное действие в процессе разборки, поэтому они в дальнейшем объединены в один блок.
Таблица 1
Пример сценария
|
Компонент/Временной интервал |
t1 |
t2 |
t3 |
t4 |
t5 |
t6 |
t7 |
t8 |
t9 |
t10 |
|
Деталь 1 | ||||||||||
|
Деталь 2 | ||||||||||
|
Деталь 3 (группа деталей A) | ||||||||||
|
Деталь 3 (группа деталей A) | ||||||||||
|
Деталь 3 (группа деталей A) | ||||||||||
|
Деталь 3 (группа деталей A) | ||||||||||
|
Деталь 4 | ||||||||||
|
Деталь 3 (группа деталей A) | ||||||||||
|
Деталь 3 (группа деталей A) | ||||||||||
|
Деталь 3 (группа деталей A) | ||||||||||
|
Деталь 3 (группа деталей A) | ||||||||||
|
Деталь 5 | ||||||||||
|
Деталь 3 (группа деталей A) | ||||||||||
|
Деталь 3 (группа деталей A) | ||||||||||
|
Деталь 3 (группа деталей A) | ||||||||||
|
Деталь 3 (группа деталей A) | ||||||||||
|
Деталь 6 | ||||||||||
|
Деталь 7 | ||||||||||
|
Деталь 8 | ||||||||||
|
Деталь 9 | ||||||||||
|
Деталь 10 |
Теперь необходимо присвоить идентификаторы. Каждой детали в составе изделия присваивается идентификатор, тем самым формируется состав изделия.
Перейдем к рассмотрению процедуры полной сборки/разборки изделия. Математическое описание этих процессов отличается незначительно — порядком действий и числом сценариев. В данном случае обратимся к процессу разборки, приняв положение о том, что существует единственный вариант. Хотя в действительности вариантов рассмотренной процедуры может быть как несколько, так и не быть вообще.
Таким образом мы составляем алгоритм, описывающий состав действий над объектами, последовательность этих действий и эффект при каждом шаге. Описание производится в виде {действие, объект; доступность, объект}, где действие может быть как простым, так и составным. В данном случае действие — съем детали.
Пусть разборка производится по следующему алгоритму:
1. Совершить действие с «Деталь 1» — d3; Доступна «Деталь 2» — d1.
2. Совершить действие с «Деталь 2» — d1; Доступна «Деталь 3» — d4.
3. Совершить действие с «Деталь 3» — d4; Доступны «Деталь 4» — d6, «Деталь 5» — d9, «Деталь 6» — d10.
4. Совершить действие с «Деталь 4» — d6; Доступна «Деталь 10» — d2.
5. Совершить действие с «Деталь 5» — d9; Доступна «Деталь 8» — d8.
6. Совершить действие с «Деталь 6» — d10; Доступна «Деталь 7» — d7.
7. Совершить действие с «Деталь 7» — d7;
8. Совершить действие с «Деталь 8» — d8;
9. Совершить действие с «Деталь 10» — d2; Доступна «Деталь 9» — d5.
2.3. Математическая постановка задачи описания доступности
Теперь мы перейти к рассмотрению графа доступности нашего виртуального продукта-изделия:
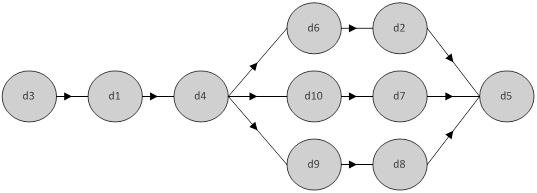
Рисунок 1. Граф доступности компонентов составного изделия
Представленный граф наглядно иллюстрирует, какие компоненты (или группы компонентов) и в какой последовательности необходимо снять, чтобы получить доступ к интересующей части изделия.
Данный граф задается:
- Матрицей 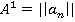
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
6 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
9 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
10 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
- Матрицей 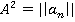
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
6 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
8 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
- Матрицей 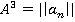
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
8 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
9 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
10 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
- Матрицей 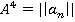
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
8 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
- Матрицей 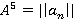
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
- Матрицей 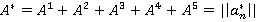
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
6 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
8 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
9 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
10 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
Мы получили матрицу 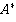 , иллюстрирующую следующую закономерность: чтобы получить доступ для совершения действия к компоненту с номером i, в процессе разборки нужно снять все компоненты, у которых присвоенное значение по матрице в строке с номером i не равно нулю.
, иллюстрирующую следующую закономерность: чтобы получить доступ для совершения действия к компоненту с номером i, в процессе разборки нужно снять все компоненты, у которых присвоенное значение по матрице в строке с номером i не равно нулю.
Поучаем число компонентов, которые мы должны снять, для выполнения условия обеспечения доступности для детали i — 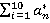 .
.
Из приведенного примера видно, что, например, для обеспечения доступности d5 нужно будет снять все остальные компоненты.
3. Заключение
Приведенная методика позволяет описать процессы монтажа-демонтажа составных компонентов сложной продукции на промышленном предприятии.
Отмечаем, что в условиях реального производства типового изделия по модульной технологии, процесс монтажа-демонтажа его компонентов производится также с учетом того, что само изделие может выступать как сложный компонент (подмножество) другого изделия более высокого уровня иерархии. Также процесс может быть усложнен дополнительными условиями физических ограничений производственной площадки и политикой предприятия.
Литература:
1. Бахтенко Е. А. Автоматизация процесса представления конструкторских данных на промышленном предприятии // Сборник статей по материалам XVIII-XIX международной заочной научно-практической конференции № 1–2(15). — М., Изд. «Международный центр науки и образования», 2014. — С. 56–60.
2. Бахтенко Е. А., Измайлов И. А. Организация информационной поддержки на промышленном предприятии // Труды Международной научно-методической конференции «Информатизация инженерного образования» — ИНФОРИНО-2014 (Москва, 15–16 апреля 2014 г.). — М.: Издательство МЭИ, 2014. — С. 27–30.
3. Латышев П. Н. Каталог САПР. Программы и производители: Каталожное издание. — М.: ИД СОЛОН-ПРЕСС, 2011. — 736 с.:ил.

