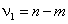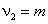Показано, что проверка гипотез о числовом значении вероятности «успеха» в схеме Бернулли и равенстве вероятностей «успеха» в двух независимых схемах Бернулли с использованием критерия 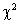 равносильна проверке тех же гипотез с использованием двустороннего критерия, основанного на нормальном приближении относительных частот «успеха».
равносильна проверке тех же гипотез с использованием двустороннего критерия, основанного на нормальном приближении относительных частот «успеха».
Ключевые слова: испытания Бернулли, вероятности «успеха», критерий 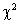 Пирсона, двусторонний критерий.
Пирсона, двусторонний критерий.
1. Вступление
Наряду с традиционной методикой, основанной на нормальном приближении относительной частоты, гипотезу о числовом значении вероятности «успеха» в схеме Бернулли можно проверить с использованием критерия Пирсона как гипотезу о распределении индикатора события. Однако в учебной литературе данная возможность почему-то не освещается. В связи с этим возникает потребность в сравнении обоих подходов.
То же самое касается и проверки гипотезы о равенстве вероятностей «успеха» в двух независимых схемах Бернулли, которую можно трактовать как гипотезу об однородности, и возможности использования для ее проверки критерия 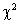 Пирсона.
Пирсона.
Сказанное и побудило автора к написанию данной статьи.
2. Постановка задачи
В данной работе ставится задача продемонстрировать «хи»-квадрат методику к проверке гипотез о числовом значении вероятности «успеха» в схеме Бернулли и равенстве вероятностей «успеха» в каких-либо двух независимых схемах Бернулли, и ее сравнение с традиционной методикой, основанной на нормальном приближении относительных частот.
Математическая постановка задач приводится в пунктах 3, 4.
3. Проверка гипотезы о числовом значении вероятности «успеха» в схеме Бернулли
Пусть в 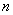 испытаниях Бернулли «успех» имел место
испытаниях Бернулли «успех» имел место 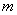 раз. Необходимо проверить нулевую гипотезу
раз. Необходимо проверить нулевую гипотезу 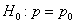 , где —
, где — 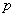 вероятность «успеха» в отдельном испытании,
вероятность «успеха» в отдельном испытании, 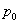 — фиксированное число (
— фиксированное число (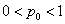 ).
).
В стандартном учебном курсе математической статистики [1] критерий проверки этой гипотезы строится на сравнении заданного числа 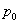 с относительной частотой «успеха»
с относительной частотой «успеха» 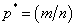 . Если
. Если 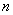 достаточно большое, а
достаточно большое, а 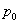 заметно отличается от 0 и 1, то в качестве статистики критерия берут статистику [1, с. 318, 2, с. 305]
заметно отличается от 0 и 1, то в качестве статистики критерия берут статистику [1, с. 318, 2, с. 305]
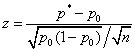 . (1)
. (1)
В формуле (1) 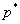 — случайная величина.
— случайная величина.
При условии правильности нулевой гипотезы 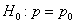 статистика (1) имеет распределение, близкое к нормальному распределению
статистика (1) имеет распределение, близкое к нормальному распределению 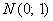 [1, с. 317, 2, с. 305].
[1, с. 317, 2, с. 305].
Критическая область для уровня значимости 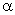 выбирается в зависимости от вида альтернативной гипотезы. В частности, для альтернативной гипотезы
выбирается в зависимости от вида альтернативной гипотезы. В частности, для альтернативной гипотезы 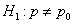 критическая область определяется неравенством [2, с. 306, 3, с. 208]
критическая область определяется неравенством [2, с. 306, 3, с. 208]
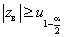 , (2)
, (2)
где 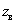 — выборочное значение статистики (1),
— выборочное значение статистики (1), 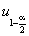 — квантиль нормального распределения
— квантиль нормального распределения 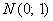 порядка
порядка 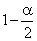 .
.
Для альтернативных гипотез 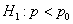 и
и 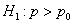 критические области определяются неравенствами
критические области определяются неравенствами 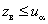 и
и 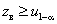 соответственно.
соответственно.
Эту же гипотезу 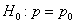 можно проверить с использованием критерия
можно проверить с использованием критерия 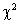 Пирсона. В связи с этим рассмотрим случайную величину
Пирсона. В связи с этим рассмотрим случайную величину 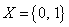 — индикатор «успеха» (
— индикатор «успеха» (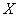 приобретает значение 1 в случае «успеха» и значение 0 в случае «неудачи»). Это позволяет сформулировать нашу гипотезу
приобретает значение 1 в случае «успеха» и значение 0 в случае «неудачи»). Это позволяет сформулировать нашу гипотезу 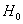 в равносильном виде
в равносильном виде
случайная величина 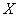 имеет распределение
имеет распределение
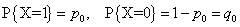 (3)
(3)
и воспользоваться критерием 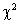 Пирсона.
Пирсона.
Пусть для проверки нулевой гипотезы (3) проведено 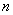 испытаний Бернулли и «успех» наступил
испытаний Бернулли и «успех» наступил 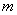 раз.
раз.
Результаты испытаний относительно случайной величины 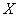 представим в виде:
представим в виде:
Таблица 1
Результаты испытаний
|
0 |
1 |
|
|
|
Область возможных значений 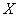 разбита на
разбита на 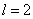 множества:
множества: 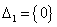 ,
, 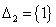 . При условии, что гипотеза
. При условии, что гипотеза 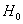 правильная,
правильная,
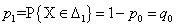 ,
, 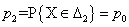 .
.
Для выборочного значения статистики критерия 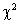 получаем
получаем
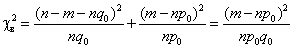 . (4)
. (4)
Это значение сравнивается с квантилем 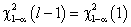 . Здесь
. Здесь 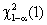 — квантиль
— квантиль 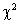 -распределения с одной степенью свободы порядка
-распределения с одной степенью свободы порядка 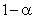 . В случае
. В случае 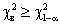 гипотеза
гипотеза 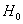 отклоняется.
отклоняется.
Теперь покажем, что критерий проверки гипотезы о числовом значении вероятности «успеха» с использованием соотношения (4) равносилен двустороннему критерию (1), (2).
Действительно, квадрат выборочного значения статистики критерия 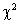 (4) равен квадрату выборочного значения статистики (1), то есть
(4) равен квадрату выборочного значения статистики (1), то есть 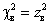 . Кроме того, справедливо равенство квантилей
. Кроме того, справедливо равенство квантилей
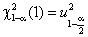 . (5)
. (5)
В результате получаем равносильность неравенств
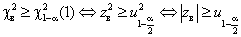 (
(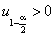 ).
).
Таким образом, нулевая гипотеза 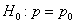 с использованием критерия
с использованием критерия 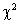 отклоняется тогда и только тогда, когда она отклоняется в случае использования двустороннего критерия (1), (2).
отклоняется тогда и только тогда, когда она отклоняется в случае использования двустороннего критерия (1), (2).
Осталось доказать равенство квантилей (5). Для этого рассмотрим случайную величину 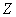 с нормальным распределением
с нормальным распределением 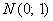 и воспользуемся равенством
и воспользуемся равенством
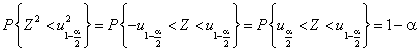 .
.
Учитывая, что по определению 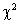 -распределения
-распределения 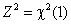 , получим
, получим
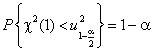 ,
,
откуда следует равенство (5).
Следует помнить, что в отличие от первого подхода методика с использованием критерия 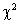 Пирсона не дает возможности строить двусторонние критерии проверки гипотезы
Пирсона не дает возможности строить двусторонние критерии проверки гипотезы 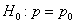 .
.
Кроме того, в соответствии с доказанным методика 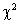 предусматривает те же условия нормального приближения относительной частоты «успеха». Если эти условия не выполняются, следует пользоваться критериями, основанными на точном (биномиальном) распределении относительной частоты.
предусматривает те же условия нормального приближения относительной частоты «успеха». Если эти условия не выполняются, следует пользоваться критериями, основанными на точном (биномиальном) распределении относительной частоты.
4. Проверка гипотезы о равенстве значений вероятностей «успеха» в двух независимых схемах Бернулли
Рассмотрим независимо друг от друга две последовательности испытаний Бернулли. Пусть в 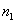 испытаниях первой последовательности событие
испытаниях первой последовательности событие 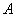 появляется
появляется 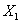 раз, а в
раз, а в 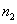 испытаниях второй последовательности —
испытаниях второй последовательности — 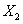 раза. Обозначим через
раза. Обозначим через 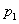 и
и 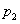 вероятности наступления события
вероятности наступления события 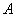 («успеха») в отдельном испытании соответственно первой и второй последовательностей. Необходимо проверить гипотезу
(«успеха») в отдельном испытании соответственно первой и второй последовательностей. Необходимо проверить гипотезу 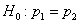 . Критерий этой проверки основывается на сравнении относительных частот «успеха»
. Критерий этой проверки основывается на сравнении относительных частот «успеха» 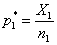 и
и 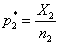 .
.
В качестве статистики критерия принимают статистику [2, с. 324, 3, с. 222]
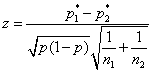 . (6)
. (6)
При условии правильности гипотезы 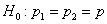 распределение этой статистики близко к нормальному распределению
распределение этой статистики близко к нормальному распределению 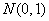 . При вычислении выборочного значения
. При вычислении выборочного значения 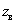 статистики (6) в качестве неизвестного параметра
статистики (6) в качестве неизвестного параметра 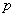 принимают оценку
принимают оценку
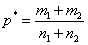 , (7)
, (7)
где 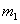 и
и 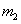 — выборочные значения величин
— выборочные значения величин 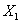 и
и 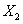 соответственно.
соответственно.
Критическая область определяется неравенствами:
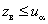 — для альтернативной гипотезы
— для альтернативной гипотезы 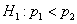 ;
;
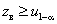 — для альтернативной гипотезы
— для альтернативной гипотезы 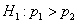 ;
;
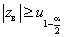 — для альтернативной гипотезы
— для альтернативной гипотезы 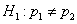 .
.
Гипотезу о равенстве вероятностей «успеха» можно проверить с помощью критерия 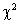 Пирсона.
Пирсона.
Предположим, что независимо друг от друга проводятся две последовательности испытаний Бернулли. Пусть в 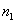 испытаниях первой последовательности «успех» появляется
испытаниях первой последовательности «успех» появляется 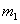 раз. Обозначим через
раз. Обозначим через 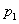 вероятность «успеха» в отдельном испытании первой последовательности. Пусть в
вероятность «успеха» в отдельном испытании первой последовательности. Пусть в 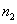 испытаниях второй последовательности «успех» появляется
испытаниях второй последовательности «успех» появляется 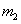 раза. Вероятность «успеха» в отдельном испытании второй последовательности обозначим через
раза. Вероятность «успеха» в отдельном испытании второй последовательности обозначим через 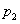 .
.
Необходимо проверить гипотезу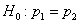 . Поскольку эта гипотеза эквивалентна гипотезе об однородности двух выборок с объемами
. Поскольку эта гипотеза эквивалентна гипотезе об однородности двух выборок с объемами 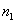 и
и 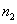 , можно воспользоваться критерием
, можно воспользоваться критерием 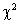 .
.
С учетом обозначений
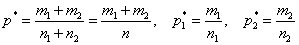
выборочное значение статистики этого критерия приобретает вид
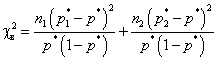 .
.
Поскольку легко убедиться в справедливости равенств
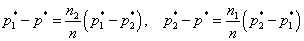 ,
,
получаем
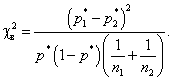 (8)
(8)
Проверка гипотезы 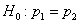 сводится к сравнению (8) с квантилем
сводится к сравнению (8) с квантилем
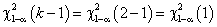 .
.
Сопоставляя (8) с выборочным значением статистики (6) при 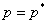 , видим, что
, видим, что 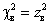 . Кроме того, справедливо равенство (5)
. Кроме того, справедливо равенство (5)
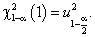
Поэтому критерий 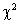 Пирсона при проверке гипотезы
Пирсона при проверке гипотезы 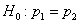 дает тот же результат, что и приведенный выше критерий (6) при альтернативной гипотезе
дает тот же результат, что и приведенный выше критерий (6) при альтернативной гипотезе 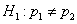 .
.
5. Выводы
На рассматриваемых в статье вопросах целесообразно акцентировать внимание в учебной литературе, а также использовать их в учебном процессе.
Литература:
1. Гмурман, В. Е. Теория вероятностей и математическая статистика: учебное пособие для вузов. 9-е изд., стер. М.: Высш. шк. — 2003. — 479 с.
2. Михайленко, В. В., Ластівка, І. О. Теорія ймовірностей і математична статистика: підручник. К.: НАУ. — 2013. — 564 с.
3. Ластівка, І. О., Михайленко, В. В. Математика для економістів: навч. посіб. у 3-х ч. Ч. 3. Теорія ймовірностей і математична статистика. К.: НАУ. — 2012. — 272 с.