Практическая и прикладная направленность модуля «Аналитическая геометрия» обеспечивается систематическим применением геометрического аппарата для решения задач на вычисление значений геометрических величин, доказательство и построение, постоянным обращением к наглядности, в частности к рисункам и чертежам на всех этапах обучения и развитием на этой основе геометрической интуиции обучающихся. Систематическое же обращение к примерам из практики развивает у них умения вычленять геометрические формы и отношения в предметах и явлениях действительности, использовать язык геометрии для их описания.
В результате изучения данного модуля студенты должны овладеть следующими умениями: изображать геометрические фигуры и тела, указанные в условиях задач, и выделять известные линии на чертежах и моделях; решать типовые задачи на вычисление и доказательство, опираясь на теоретические сведения, полученные в данном модуле; проводить доказательные рассуждения в ходе решения типовых задач; вычислять значения геометрических величин (длин, углов, площадей, расстояний), применяя изученные свойства и формулы; применять аппарат алгебры, начал анализа и тригонометрии в ходе решения задач; использовать векторы и координаты для решения задач (вычисление длин и углов, операции над векторами); изображать геометрические тела, вычислять их объемы и площади поверхностей.
Блок входного контроля в модуле «Аналитическая геометрия» реализуется через повторение соответствующего материала школьного курса планиметрии и стереометрии, вводную проверку знания определений основных понятий, формул и теорем с целью диагностики уровня сформированности системы знаний, необходимых для изучения данного модуля. С этой целью студентами можно предложить тестовую работу следующего характера.
1. Коллинеарными называют векторы:
А) лежащие на перпендикулярных прямых;
Б) лежащие на одной или параллельных прямых;
В) лежащие на одной прямой.
2. Если векторы перпендикулярны, то их скалярное произведение:
А) равно 0; Б) равно 1; В) не существует.
3. Общее уравнение прямой на плоскости имеет вид:
А) у=Ах + В; Б) Ах=Ву; В) Ах+Ву+С=0.
2. Выпишите прямые, параллельные данной прямой у=5х+7:
А) у-5х=2; Б) 1/5х+у+7=0; В) 5х-у=7.
3. Сколько общих точек имеют при пересечении две плоскости:
А) две; Б) одну; В) «целую прямую» точек.
4. Выберите те способы, которыми можно задать плоскость в пространстве:
А) через три точки;
Б) через две пересекающиеся прямые;
В) через прямую и точку, не лежащую на ней.
5. В прямоугольном треугольнике отрезки, на которые высота, опущенная из вершины прямого угла, делит гипотенузу, равны 6 и 18. Найти площадь треугольника.
А) 72Ö3; Б) 60; В) 72.
6. Даны вершины А(2;-1;4), В(3;2;-6), С(-5;0;2) треугольника. Вычислить длину его медианы, проведенной из вершины А.
А) 9; Б) 7; В) 16.
 Теоретический блок краткого изложения содержит в себе перечень основных тем модуля, наглядно представленных обучающимся в виде структурных схем. Студенты здесь получают возможность познакомиться с темой, структурой изучения раздела, объемом учебного времени, отводимым на изучение той или иной его составляющей. При этом осуществляется повторение необходимых для изучения в рамках модуля известных ранее математических понятий (координатная плоскость, прямая, параллельные прямые, перпендикулярные прямые и т. д.), формул (площадей, длины дуги и др.), теорем (Пифагора, теорема о трех перпендикулярах и т. д.). Для наглядной иллюстрации содержания модуля приводится следующая опорная схема (рис.1).
Теоретический блок краткого изложения содержит в себе перечень основных тем модуля, наглядно представленных обучающимся в виде структурных схем. Студенты здесь получают возможность познакомиться с темой, структурой изучения раздела, объемом учебного времени, отводимым на изучение той или иной его составляющей. При этом осуществляется повторение необходимых для изучения в рамках модуля известных ранее математических понятий (координатная плоскость, прямая, параллельные прямые, перпендикулярные прямые и т. д.), формул (площадей, длины дуги и др.), теорем (Пифагора, теорема о трех перпендикулярах и т. д.). Для наглядной иллюстрации содержания модуля приводится следующая опорная схема (рис.1).
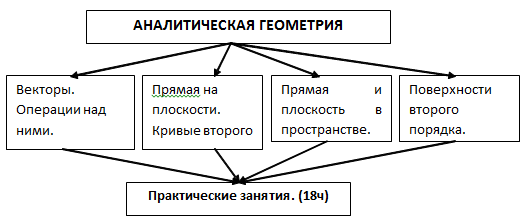
Рис.1
Теоретический блок работы с учебными элементами содержит в себе все лекционные занятия по модулю «Аналитическая геометрия». Учебный материал выдается в виде лекции, содержание которого тщательно анализируется, после чего выделяются доминирующие элементы знания.
Большую роль в таком обучении играет опорная таблица с основными понятиями и определениями, которые должны знать учащиеся по модулю «Аналитическая геометрия». Данная таблица выдается каждому студенту в начале лекции. В ходе лекции они дополняют ее получаемой информацией и разъясняют каждый ее пункт.Приведем пример заполненной опорной таблицы лекции «Линии и поверхности», табл.1.
Таблица 1
|
Темы модуля |
Основные понятия |
|
Прямая на плоскости. Кривые второго порядка.(4ч) |
Уравнением линии (кривой) на плоскости Оху называется уравнение F(x;y)=0, которому удовлетворяют координаты х и у каждой точки этой линии и только они. Виды уравнения прямой на плоскости. Углом между прямыми в плоскости понимают наименьший(острый) из двух смежных углов, образованными этими прямыми. Условия параллельности и перпендикулярности двух прямых, пересечение прямых, расстояние от точки до прямой. Линии, определяемые алгебраическими уравнениями второй степени относительно переменных х и у называются кривыми второго порядка. Окружность, эллипс, гипербола, парабола. |
|
Прямая и плоскость в пространстве(4ч). |
Уравнением поверхности в пространстве Oxyz называется уравнение F(x,y,z)=0, которому удовлетворяют координаты каждой точки поверхности и только они. Каждая плоскость в пространстве Oxyz определяется линейным алгебраическим уравнением первой степени с тремя неизвестными. Виды уравнения плоскости. Угол между двумя плоскостями, условия параллельности и перпендикулярности двух плоскостей, расстояние от точки до плоскости. Различные виды уравнения прямой в пространстве. Угол между двумя прямыми, условия параллельности и перпендикулярности прямых, условие компланарности. Угол между прямой и плоскостью. Взаимное расположение прямой и плоскости. |
|
Поверхности второго порядка(2ч) |
Если F(x,y,z) — многочлены не выше второй степени относительно совокупности переменных x, y, z, то уравнение F(x,y,z)=0 называется уравнением второго порядка, а поверхность, изображаемая этим уравнением называется поверхностью второго порядка. Поверхности второго порядка: сфера, эллипсоид, однополостный гиперболоид, двуполостный гиперболоид, параболоид, параболоид гиперболический, конус эллиптический, цилиндры: эллиптический, гиперболический, параболический. |
После ознакомления с основными понятиями, формулами и графиками происходит переход к закреплению и углублению полученных знаний. Реализуется блок применения. Чтобы эффективно систематизировать математические знания по данной теме, работа в данном блоке модуля предполагает реализацию системно-структурного подхода к усвоению знаний через построение соответствующих структурных схем. Данный компонент усвоения знаний, как уже указывалось выше, предусматривает отказ от поэтапного изучения материала маленькими порциями в пользу изложения большими блоками. При большом объеме теоретического материала число отдельных учебных занятий при этом можно свести к минимуму, уменьшая временной разрыв, что очень важно для целостного восприятия теоретического материала. С блоком применения тесно связан блок углубления. Студенты, хорошо усвоившие решения типичных задач (необходимый минимум), способны повысить свой рейтинговый показатель за счет работы с дополнительной литературой и решения задач повышенной сложности.
На заключительном этапе изучения данного модуля мы должны оценить полученные студентами знания, для этого существует блок выходного контроля, который выполняет диагностирующие функции. В модуле «Аналитическая геометрия» осуществляется текущий контроль в виде самостоятельных работ по каждой теме и итоговый — в виде типового расчета по всем темам модуля. После итогового контроля происходит анализ и подведение итогов достижения целей обучения, коррекция, определение перспективы дальнейшей работы.
Литература:
1. Ермолаева Е. И. Проблемы усвоения математических знаний студентами технических вузов// Актуальные проблемы гуманитарных и естественных наук, № 7, 2010г. С. 270–272.
2. Ермолаева Е. И. Систематизация математических знаний у студентов строительных специальностей в рамках модульного обучения// Наука и школа. 2008. № 1. С. 33–37.
3. Ермолаева Е. И. Особенности реализации модульного обучения в системе высшего образования// В мире научных открытий. 2010. № 4–5. С. 109–110.

