В случае неразрушающего контроля активными тепловыми методами, искомые теплофизические свойства (ТФС) проявляются через температурный отклик (термограмму) исследуемого объекта на тепловое воздействие, которому подвергается образец (или изделие) в специально организованном эксперименте. Реализация тепловых методов НК ТФС усложняется еще и тем, что тепловое воздействие и получение измерительной информации в ходе эксперимента возможно осуществлять только на ограниченном участке поверхности исследуемого объекта.
В методе неразрушающего контроля (НК) теплофизических свойств (ТФС) твердых материалов, измерительная схема которого представлена на рис. 1, тепловое воздействие на исследуемое тело с равномерным начальным распределением температуры осуществляется с помощью нагревателя постоянной мощности, встроенного в подложку измерительного зонда (ИЗ). В эксперименте фиксируется избыточная температура Т исследуемого тела в центре нагревателя и на расстояниях r1 и r2 от центра [1–3].

Рис. 1. Измерительная схема
Известно, что распределение температуры в исследуемом теле от плоского круглого источника тепла постоянной мощности радиусом Rп при t>>0 близко к распределению температуры в сферическом полупространстве со сферической полостью радиусом R, через которую осуществляется заданное тепловое воздействие с тем же удельным тепловым потоком q [4, 5].
Расчетное уравнение, описывающее распределение температуры в плоскости контакта двух полуограниченных тел от сферического источника тепла, получено решением соответствующей краевой задачи и имеет вид [6]:
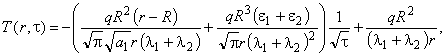
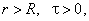 (1)
(1)
где a1, l1, e1, a2, l2, e2 — соответственно температуропроводности, теплопроводности и тепловые активности материалов исследуемого тела и подложки ИЗ; r — координата;
t — время.
При определении условий адекватности модели сферического полупространства реальному тепловому процессу найдено, что соотношение радиусов R и Rп, при котором температурные поля, создаваемые сферическим поверхностным и круглым плоским нагревателями, будут идентичными, имеет вид [6]:
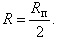 (2)
(2)
Решение уравнения (1), полученное для сферического источника тепла, при r = R имеет вид:
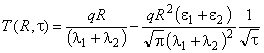 . (3)
. (3)
При исследовании температурных полей в системе измерительный зонд — изделие авторы воспользовались численным моделированием двумерных полей методом конечных элементов с помощью пакета ELCUT [7].
В качестве материала исследуемого изделия был выбран политетрафторэтилен (ПТФЭ) со следующими ТФС: теплопроводность l1 = 0,25 Вт/м×К; удельная теплоемкость с1 = 1005 Дж/кг×К; плотность r1 = 2200 м3/кг. Материалом подложки измерительного зонда является пенополиуретан типа Рипор: l2 = 0,028 Вт/м×К; с2 = 1270 Дж/кг×К; r2 = 50 кг/м3.
Моделирование проводилось при следующих условиях: время нагрева t = 500 с; удельный тепловой поток q = 5000 Вт/м2; радиус поверхностного сферического нагревателя R = 0,002 м; радиус плоского нагревателя Rп=0,004 м. Между телами задавался идеальный тепловой контакт. Размеры тел подбирались так, чтобы внешние границы не влияли на формирование температурного поля и соблюдались условия полуограниченности.
Температурные поля в системе двух тел с одинаковыми ТФС (ПТФЭ — ПТФЭ) при нагреве от поверхностного сферического и плоского круглого нагревателя представлены на рис. 2 и 3, соответственно.
Из рис. 2 и 3 видно, что при больших значениях времени и r > Rп распределение температуры от плоского круглого источника тепла постоянной мощности идентично распределению температуры от поверхностного сферического нагревателя с тем же удельным тепловым потоком.
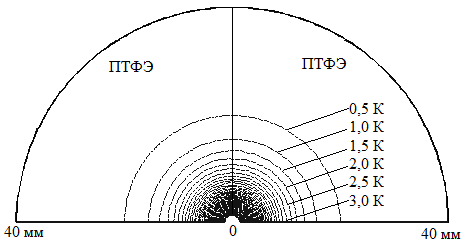
Рис. 2. Температурное поле от поверхностного сферического нагревателя постоянной мощности в системе двух тел с одинаковыми ТФС
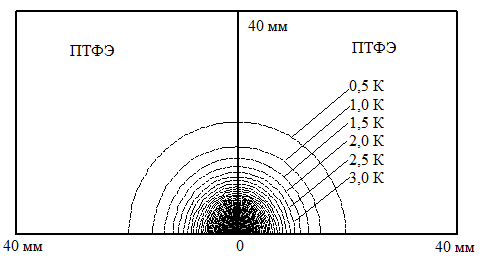
Рис. 3. Температурное поле от плоского круглого нагревателя постоянной мощности в системе двух тел с одинаковыми ТФС
Авторами также проведено численное моделирование тепловых систем с плоским круглым нагревателем постоянной мощности, находящимся между двух полуограниченных тел с различными ТФС (Рипор и ПТФЭ) в следующих случаях: идеальный тепловой контакт тел; идеальная теплоизоляция между телами.
На рис. 4 представлено температурное поле, полученное при следующих условиях: идеальный тепловой контакт между телами из Рипора и ПТФЭ; t = 500 с; q = 5000 Вт/м2; Rпл = 0,004 м.
На рис. 5 представлено температурное поле, полученное при следующих условиях: идеальная теплоизоляция между телами из Рипора и ПТФЭ; t = 100 с; q = 5000 Вт/м2; Rпл = 0,004 м.
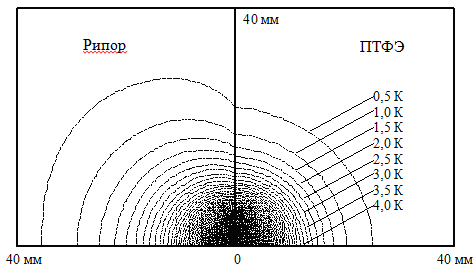
Рис. 4. Температурное поле от плоского круглого нагревателя постоянной мощности при идеальном тепловом контакте между телами с разными ТФС и t = 500 с.
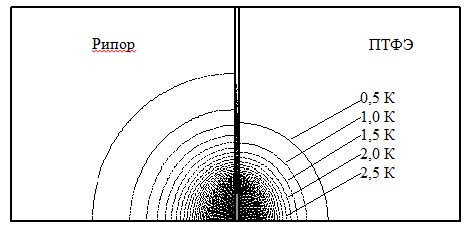
Рис. 5. Температурное поле от плоского круглого нагревателя постоянной мощности при идеальной тепловой изоляции между телами с разными ТФС и t = 100 с.
Определение условий адекватности математической модели сферического полупространства реальному тепловому процессу от плоского круглого источника тепла [1], визуализация температурных полей в системе зонд — изделие позволили применить расчетные зависимости (1), (3) на рабочих участках термограмм в зондовом контактном методе неразрушающего контроля ТФС [1–3].
Реализация разработанного метода НК ТФС экспериментально осуществлялась с применением измерительной системы, схема и описание принципа работы которой детально представлены в работах [6, 8].
Литература:
1. Жуков Н. П., Майникова Н. Ф., Муромцев Ю. Л., Рогов И. В., Орлов В. В. Способ комплексного определения теплофизических свойств материалов // Патент на изобретение RUS № 2167412 22.02.1999.
2. Жуков Н. П., Рогов И. В., Чех А. С., Никулин С. С., Майникова Н. Ф. Способ неразрушающего определения теплофизических свойств твердых материалов // Патент на изобретение RUS № 2328725 17.11.2006.
3. Майникова, Н. Ф. Об одном методе термического анализа для неразрушающего контроля теплофизических свойств полимеров / Н. Ф. Майникова, Ю. Л. Муромцев, И. В. Рогов, А. А. Балашов // Пластические массы. — 2001. — № 1. — С. 30–33.
4. Жуков, Н. П. Моделирование процесса теплопереноса от плоского источника тепла постоянной мощности при теплофизических измерениях / Н. П. Жуков, Н. Ф. Майникова // Инженерно-физический журнал. — 2005. — Т.78, № 6. — С. 56–63.
5. Жуков, Н. П. Многомодельный метод неразрушающего определения теплофизических свойств материалов / Н. П. Жуков, Н. Ф. Майникова, И. В. Рогов, Е. В. Пудовкина // Инженерно-физический журнал. — 2012. — Т.85, № 1. — С. 188–194.
6. Жуков, Н. П. Многомодельные методы и средства неразрушающего контроля теплофизических свойств материалов и изделий / Н. П. Жуков, Н. Ф. Майникова. — М.: Машиностроение-1, 2004. — 288 с.
7. ELCUT / Руководство пользователя. СПб, 2003. 231 с.
8. Жуков, Н. П. Измерительно-вычислительная система неразрушающего контроля теплофизических свойств / Н. П. Жуков, Н. Ф. Майникова // Приборы и техника эксперимента. — 2005. –№ 4. — С. 164–166.

