Пусть неизвестный генотип по одному признаку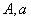 
скрещивается с доминантной особью, и его потомок опять скрещивается с доминантной и так далее. Надо найти распределение вероятностей каждого из возможных генотипов в 
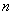-ом поколении (см.
). Как известно, составлен таблица вероятностей перехода к возможным генотипам (различные строки — это вероятности возможных генотипов скрещиваемого, имеющим генотип 
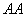, столбцы — возможные вероятности генотипов потомства):
|
|
|
| |
|
|
1 |
0 |
0 |
|
|
|
|
0 |
|
|
0 |
1 |
0 |
Таблица означает, что генотип 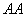при скрещивании с генотипом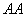 
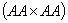даёт потомок с вероятностью 1, 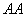с 
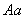
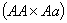даёт потомок 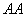с вероятностью 
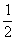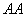, с 
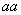
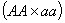даёт потомок 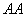с вероятностью о и так далее (первый столбец).
Обозначим через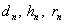 
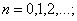, соответственно, вероятности генотипа (доминантный), (гитрозиготный), (рецессивный), 
и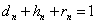 
.
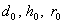являются исходными вероятностями неизвестной особи, соответственно.
Для получение вероятностей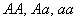 
в потомстве суммируем вероятности этого генотипа при различных возможных генотипах неизвестной особи (по столбцу таблицы). Для получение вероятности генотипа 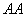в первом поколении берём вероятность получения этого генотипа при условии, что генотип неизвестной особи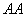 
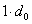, и прибавим вероятностной особи 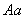, т. е. 
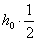. Тогда вероятность получения в первом поколении при скрещивании равно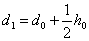 
.
Аналогично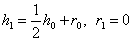 
.
Для получения вероятностей следующего поколения мы воспользуемся с той же таблицы.
Получим: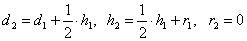 
.
Поставляя значения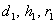 
, имеем
, 
, 
.
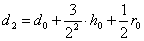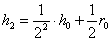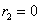Аналогично, для 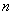–го поколения скрещивания с , имеем:
, 
, 
.
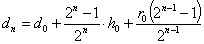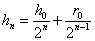Отсюда следует теорема:
ТЕОРЕМА-1.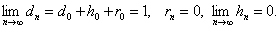 
Если неизвестный особь скрещивается с особью с генотипом и в результате вероятность того, что получается 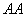равно: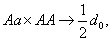 
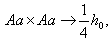
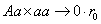, суммируя имеем:
.
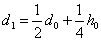Аналогично, вероятность того, что имеем генотип 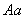, равно
,
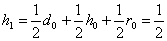а для генотипа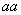
.
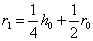Для второго поколения
,
,
.
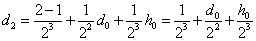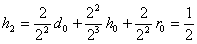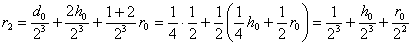Для 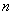-ного поколения скрещивания с 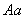имеем
.
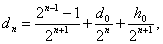
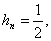
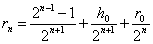Отсюда следует
ТЕОРЕМА-2. 
Если неизвестный особь скрещивается с особью с генотипом и в результате вероятность того, что в -ом поколении получается, соответственно, генотипы 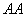, , 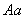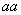равно
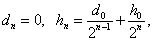
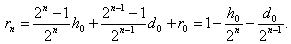
Тогда имеет место:
ТЕОРЕМА-3.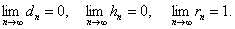 
В частности, при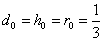 
приведем таблицу для 
.
|
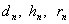n |
1 |
2 |
3 | ||||||
|
d(n) |
h(n) |
r(n) |
d(n) |
h(n) |
r(n) |
d(n) |
h(n) |
r(n) | |
|
1 |
0,5 |
0,5 |
0 |
0,25 |
0,50 |
0,25 |
0 |
0,5 |
0,5 |
|
2 |
0,75 |
0,25 |
0 |
0,25 |
0,50 |
0,25 |
0 |
0,25 |
0,75 |
|
3 |
0,875 |
0,125 |
0 |
0,25 |
0,50 |
0,25 |
0 |
0,125 |
0,875 |
|
4 |
0,9375 |
0,0625 |
0 |
0,25 |
0,50 |
0,25 |
0 |
0,0625 |
0,9375 |
|
5 |
0,96875 |
0,03125 |
0 |
0,25 |
0,50 |
0,25 |
0 |
0,03125 |
0,96875 |
|
6 |
0,984375 |
0,015625 |
0 |
0,25 |
0,50 |
0,25 |
0 |
0,015625 |
0,984375 |
|
7 |
0,9921875 |
0,0078125 |
0 |
0,25 |
0,50 |
0,25 |
0 |
0,0078125 |
0,9921875 |
|
8 |
0,99609375 |
0,00390625 |
0 |
0,25 |
0,50 |
0,25 |
0 |
0,00390625 |
0,99609375 |
|
9 |
0,998046875 |
0,00195313 |
0 |
0,25 |
0,50 |
0,25 |
0 |
0,001953125 |
0,998046875 |
|
10 |
0,999023438 |
0,00097656 |
0 |
0,25 |
0,50 |
0,25 |
0 |
0,000976563 |
0,999023438 |
Заключение: Из таблицы видно, что неизвестный особь при скрещивание с 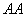имеет вероятность 
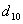, очень близкое единице, следовательно, 
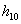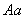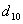близко к нулю, если скрещивание происходит с , то и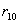 
близки к 
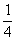, при скрещивании с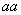 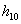близко к нулю,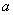 
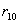близко к единице.
Литература:
1. Нейман Ю. Вводный курс теории вероятностей и математической статистики. Из. «Наука», М. 1968.
2. Математика и естествознание, Из. «Просв»., М. 1969.
3. Marek Kimmel, David E. Axelrod. Branching Processes in Biology. Springer. 2002.
