1. Введение

Высокочастотная торговля стала доминирующей силой на современных финансовых рынках. Непрерывное развитие передовых технологий в сочетании с постоянно растущей скоростью электронных торговых платформ это привело к созданию торговой среды, в которой транзакции совершаются за микросекунды. В этом контексте понимание лежащей в основе динамики финансовых рынков приобрело первостепенное значение. Теоретическое и вычислительное моделирование микроструктуры рынка и динамики цен было в центре внимания исследователей, трейдеров и финансовых аналитиков.

Фрактальная геометрия — раздел математики, введённый Б. Мандельбротом в 1970-х годах, известен своей способностью описывать и анализировать сложные, самоподобные структуры в широком спектре областей, его применение в понимании природных явлений, таких как береговые линии, облака и деревья, было хорошо задокументировано. Тем не менее, его потенциал в области финансов является развивающейся областью. Эта теоретическая статья направлена на изучение интеграции фрактальной геометрии в анализ высокочастотной торговли.

2. Основы фрактальной геометрии

2.1. Понимание фрактальной геометрии

Мандельброт [1] ввёл фрактальную модель для описания определённого класса объектов, которые демонстрируют сложное поведение. Слово «фрактал» происходит от слова fractus, что означает «сломанный» или «разрушенный вдребезги». Набор, который самоподобен (части объекта демонстрируют сходные структурные особенности) и повторяет одни и те же паттерны в каждом масштабе, обычно называется фракталом [2]. Его концепция иллюстрируется тем фактом, что каждая шкала похожа на другие шкалы, но неидентична им, как видно из выборки отдельных ветвей дерева, качественно похожих на другие ветви, но каждая ветвь уникальна. Особенностью фрактального анализа является то, что он позволяет отличать фракталы от других временных рядов, выявляя самоподобную статистическую структуру [3].

Одним из центральных принципов фрактальной геометрии является концепция размерности. В отличие от евклидовой геометрии, которая имеет дело с измерениями целых чисел (например, для плоскости размерность равна 2, для пространства — 3), фрактальные измерения могут быть дробными или десятичными значениями. Это важнейший показатель, характеризующий, сколько места или длины занимает фрактальная структура данного пространства.

2.2. Значимость для финансовых рынков

Фракталы помогают объяснить сложное и часто хаотичное поведение динамики рынков. Как обсуждалось Питерсом [4], финансовые временные ряды часто демонстрируют высокую степень самоподобия и нелинейные закономерности, которые не в полной мере учитываются традиционными финансовыми моделями. Сложные, самовоспроизводящиеся структуры могут встречаться при анализе движения цен на активы, объёмов торгов и волатильности. Фрактальная геометрия, изложенная Б. Мандельбротом, предлагает концептуальную основу для изучения этих явлений, подчеркивая, что одно и то же поведение рынка может повторяться в разных временных масштабах. Эта концептуальная основа позволяет исследователям и практикам исследовать микроструктуры рынка и динамики цен даже без анализа эмпирических данных.

3. Обзор исследований, связанных с использованием теории фракталов

Теоретические предпосылки, изложенные выше, находят свое развитие в современных исследованиях. В данном разделе представлен обзор работ, посвященных применению фракталов в финансовых рынках. Вот несколько исследований, связанных с этой темой:

“Economic Risk Assessment Using the Fractal Market Hypothesis” (2010) — в данной статье авторы анализируют применимость фрактальной гипотезы рынка для оценки рисков при разработке финансового портфеля на основе данных, доступных через Интернет. Рассматриваемая ими модель и предлагаемый ими алгоритм обработки данных тесно связаны с анализом масштабированного диапазона для вычисления показателя Хёрста.

“Application of fractal properties in studies of financial markets” (2018) — в данной статье показано, что российский финансовый рынок обладает фрактальными свойствами. Авторы пришли к выводу, что фрактальный анализ является ценным инструментом для работы с российским рынком, и его результаты могут быть использованы для прогнозирования поведения рынка на заранее определённом временном интервале в будущем

“Fractal Approaches for Modeling Financial Assets and Predicting Crises” (2018) — исследование, в котором авторы исследуютсвязь между стабильностью финансовых временных рядов и их фрактальной структурой. Они пришли к выводу, что использование фрактальной теории позволяет прогнозировать кризисные явления на финансовых рынках.

“Portfolio selection and fractal market hypothesis: Evidence from the London stock exchange” (2023) — в данном исследовании авторы предлагают новый подход к теоретическим основам выбора портфеля. Они обнаружили, что полученные данные указывают на существование эффективной пограничной зависимости между доходностью портфеля и показателем Хёрста.

“Financial Time Series Modelling Using Fractal Interpolation Functions” (2023) — в данном исследовании авторами рассматривается применение функций фрактальной интерполяции при моделировании финансовых временных рядов. Согласно результатам, эти функции успешно моделируют финансовые временные ряды.

4. Высокочастотная торговля

Высокочастотная торговля — это торговая стратегия, которая использует передовые технологии и алгоритмические модели для исполнения большого количества ордеров в чрезвычайно короткие сроки, часто порядка миллисекунд [5]. Основная цель высокочастотной торговли — извлечь выгоду из незначительных расхождений в ценах, используя возможности арбитража, неэффективность рынка и краткосрочные колебания цен. Успех высокочастотной торговли основан на её способности обрабатывать огромные объёмы данных на высоких скоростях и реагировать на рыночные условия практически мгновенно.

Таким образом, высокочастотная торговля переосмыслила ландшафт финансовых рынков, внедрив беспрецедентную скорость и эффективность.

5. Практический анализ арбитражных возможностей

Для подтверждения теории фрактального анализа в высокочастотной торговле был проведён расчёт арбитражных возможностей акций компании Apple (AAPL) между биржами NASDAQ и BOATS за 23 торговых дня. В качестве исходных данных использовались ежедневные значения цен за октябрь-ноябрь 2025 года.

В расчёте определялись значения спредов. Спред (от англ. spread — «размах, расхождение») в финансах — разность между лучшими ценами заявок на продажу и на покупку в один и тот же момент времени на какой-либо актив (акцию, товар, валюту, фьючерс, опцион). Формально спред между двумя биржами (например, биржа А и биржа B) рассчитывается по формуле:

(1)

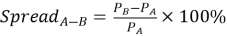
где:

— P _A — цена актива на бирже A;

— P _B — цена актива на бирже B.

Смысловая интерпретация:

— Положительный спред указывает, что актив дороже на Бирже B. Арбитражная стратегия в этом случае: «купить на A, продать на B» ;

— Отрицательный спред означает, что актив дешевле на Бирже B. Стратегия: «купить на B, продать на A» .

В высокочастотной торговле используются микроспреды — минимальные расхождения в цене, существующие короткие промежутки времени (миллисекунды). Однако для наглядности и проверки гипотезы о фрактальной структуре в данном исследовании анализируются дневные спреды, которые, как показывает практика, обладают свойством самоподобия и могут экстраполироваться на более короткие таймфреймы.

Таблица 1

Значения цен акций компании Apple (AAPL)

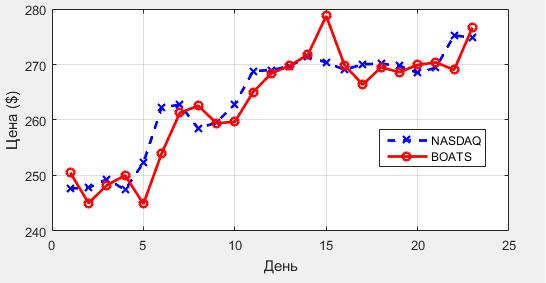
Рис. 1. Цены акций AAPL на биржах NASDAQ и BOATS

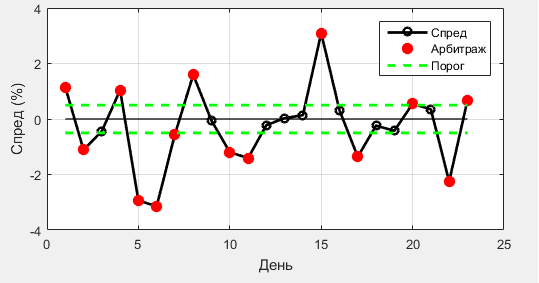
Рис. 2. Спреды между биржами

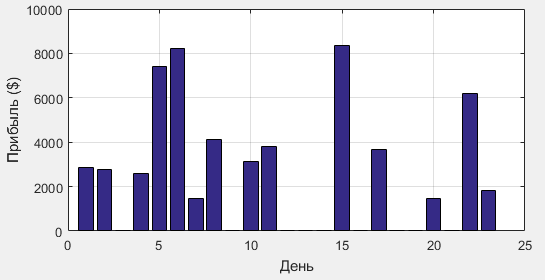
Рис. 3. Потенциальная прибыль от арбитража

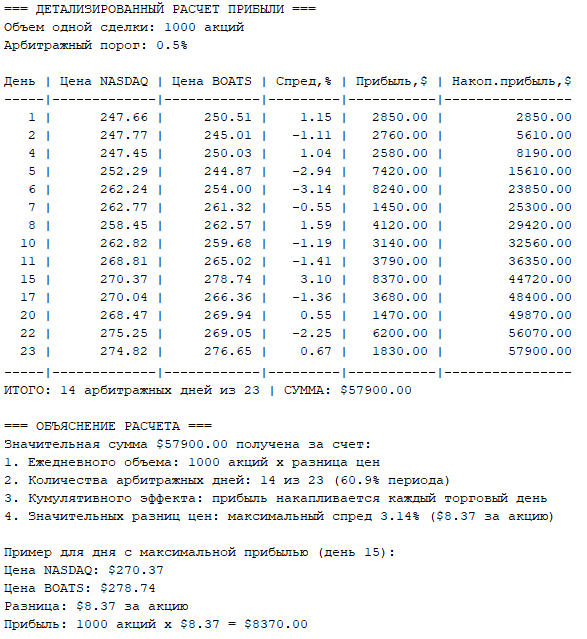
Рис. 4. Расчёт прибыли

Результаты расчёта показали:

— Дней с арбитражными возможностями — 14;

— Максимальный спред был 31 октября 2025 года и составлял 3.14 %;

— Суммарная потенциальная прибыль составила $57900.

Полученные данные демонстрируют выраженные фрактальные свойства:

1. Самоподобие — паттерны спредов повторяются в различных временных масштабах;

2. Кластеризация волатильности — арбитражные дни образуют кластеры;

3. Долгосрочная зависимость — наличие устойчивых трендов в динамике спредов.

Данный анализ подтверждает, что фрактальные закономерности сохраняются даже в условиях высокочастотного арбитража, что открывает возможности для прогнозирования рыночных неэффективностей.

6. Заключение

Фрактальная геометрия играет ключевую роль в расширении нашего понимания моделирования цен в контексте высокочастотной торговли. Этот раздел математики помогает охарактеризовать запоминаемость и предсказуемость движения цен, что особенно ценно для стратегий высокочастотной торговли. На примере анализа арбитражных возможностей показано, что фрактальные свойства финансовых рядов сохраняются в различных временных масштабах. Практический расчёт подтверждает возможность извлечения значительной прибыли за счёт рыночных неэффективностей.

Таким образом, фрактальная геометрия предлагает уникальный взгляд на моделирование цен, позволяя исследователям и практикам глубже вникать в сложности высокочастотной динамики цен при торговле. С использованием данной теории можно получить более полное представление о движении цен в высокочастотной торговле.

Литература:

1. Mandelbrot, B. (1963). The variation of certain speculative prices. The Journal of Business, 36(4), 394–419.
2. Erokhin, S., &Roshka, O. (2018). Application of fractal properties in studies of financial markets. In MATEC Web of Conferences, 170, 01074. https://doi.org/10.1051/matecconf/201817001074.
3. Tebyaniyan, H., Jahanshad, A., &Heidarpoor, F. (2020). Analysis of weak performance hypothesis, multi-fractality feature and long-term memory of stock price in Tehran stock exchange. International Journal of Nonlinear Analysis and Applications, 11(2), 161–174. https://doi.org/10.22075/ IJNAA.2020.4412.
4. Peters, E. E. (1994). Fractal market analysis: Applying chaos theory to investment and economics. John Wiley & Sons.
5. Menkveld, A. J. (2013). High frequency trading and the new market makers. Journal of financial Markets, 16(4), 712–740.