В настоящее время на территории Российской Федерации расположено значительное количество различных радиационно опасных объектов (атомных электростанций, промышленных предприятий ядерного топливного цикла, пунктов хранения ядерных материалов и т. д.). По некоторым данным число объектов указанного типа составляет более 250 [1, 2]. Эксплуатация данных объектов связана с рисками возникновения на них различного рода аварий (разрушений) вследствие причин техногенного характера, террористических актов, преднамеренного разрушения в ходе ведения боевых действий. В результате, может сложиться неблагоприятная радиационная обстановка и, как следствие, необходимость оценки её влияния на население и войска (проведение оценки радиационной обстановки).

При оценке радиационной обстановки, сложившейся в результате аварий (разрушений) на радиационно опасном объекте используется большое количество исходных данных, одним из которых является доза облучения, получаемая населением (персоналом, личным составом войск) после аварии на радиационно опасном объекте при открытом расположении в середине зоны загрязнения. Расчеты дозы облучения, получаемой населением (персоналом, личным составом) после аварии на радиационно опасном объекте при открытом расположении в середине зоны загрязнения, выполняются с использованием табличных данных, показанных в таблице 1 [3]. Показатели доз облучения в таблице представлены дискретно, для фиксированных значений временных показателей, как для продолжительности пребывания в зоне загрязнения, так и для времени начала облучения после аварии. Таким образом, точно определить значение дозы облучения, например, для параметров: 60 часов «время начала облучения после аварии» и 60 часов «пребывания в зоне загрязнения» с достаточной степенью точности, не представляется возможным, т. к. табличные значения для них отсутствуют.

Таблица 1

Показатели доз облучения (Рад)

Получение дозы облучения для временных показателей, находящихся между дискретных значений может быть выполнено со значительными погрешностями. Также выбор временного показателя не является линейной задачей, поскольку табличные данные представлены в виде нелинейной зависимости, начиная с первого часа до 12 месяцев. Кроме того, табличные данные используются в работе специального программного обеспечения, реализующие функции оценки радиационной обстановки. Данный подход накладывает существенные ограничения на использование его возможностей в полной мере (отсутствует возможность проведения точных расчётов при отсутствии в таблицах необходимых значений).

Исходя из вышеизложенного, актуальным является получение параметра «доза облучения» для произвольных значений временных показателей. Для рассматриваемого случая данные находятся в виде отдельных узловых точек, координаты которых заданы временными показателями в таблице. Необходимо получить описание неявно заданной зависимости с помощью более простой или более единообразной зависимости. Данная задача может быть решена в результате аппроксимации табличных данных для определения доз излучения в произвольные моменты времени.

Существует достаточно большое количество методов аппроксимации, применимых, в том числе, к табличной форме представления данных. Можно привести в качестве примера метод наименьших квадратов. В этом методе при сглаживании табличных данных аппроксимирующую поверхность стремятся расположить так, чтобы её отклонения от дискретных данных по всем узловым точкам были минимальными. Однако, для многомерных данных применение таких методов становится трудоемким. Более простыми, но не менее эффективными являются методы, использующие технологии искусственного интеллекта. Среди них можно выделить методы, основанные на применении искусственных нейронных сетей. Создание и использование нейронных сетей в современных вычислительных средах осуществляется достаточно просто. Для решения задачи аппроксимации двумерных табличных данных с помощью одной из технологий искусственного интеллекта применяется вычислительная среда MatLab, причём предварительно выполняется адаптация исходных данных для работы в вычислительной среде.

Исходные данные — дозы облучений, получаемые населением (персоналом, личным составом) после аварии на радиационно опасном объекте при открытом расположении в середине зоны загрязнения — представляют собой матрицу размером 20×21. В качестве координаты X принимается временной показатель продолжительности пребывания в зоне загрязнения. Тогда координатой Y тогда будет время начала облучения после аварии. Для снижения эффекта нелинейности временных шкал показатели обоих координат прологарифмированы.

Среди модификаций нейронных сетей существует бесконечное количество функций, которые могут моделировать конечный набор пар данных и их диапазонов. Отмечается [4, 5], что радиальные базисные нейронные сети весьма эффективно используются для аппроксимации функций. Преимущество радиальной базисной нейронной сети перед другими типами состоит в том, что ее функционал обеспечивает добавление нейронов в скрытый слой до тех пор, пока она не достигнет заданного значения среднеквадратичной ошибки.

Кроме того, синтаксис радиальной базовой нейронной сети в вычислительной среде MatLab предполагает использование коэффициента распространения радиальных базисных функций. Чем больше это распространение, тем более плавной будет аппроксимация функции. Слишком большое распространение означает, что для соответствия быстро меняющейся функции потребуется много нейронов. Слишком малое распространение означает, что для выполнения плавной функции потребуется много нейронов, и сеть может плохо обобщать. Величина коэффициента определяется в ходе подбора опытным путем при получении оптимального результата аппроксимации.

Например, если коэффициент распространения равен «2», то каждый нейрон скрытого слоя радиальной базисной сети будет реагировать на любые входные векторы на расстоянии «2» от своего вектора веса.

Архитектура радиальной базисной нейронной сети состоит из двух слоев, как показано на рисунке 1: первый — радиально-базисный с количеством нейронов S ; второй — линейный слой с количеством нейронов T . Размерность вектора входного сигнала R .

В первом слое рассчитывается векторное расстояние между его весовыми коэффициентами и входным вектором , умноженное на смещение . Радиальная базисная функция будет максимальной, т. е. равна 1, когда ее входной сигнал равен 0. Поскольку расстояние при обучении нейронной сети между и уменьшается, функция увеличивается. Таким образом, радиальный базисный нейрон действует как детектор, который выдает единицу всякий раз, когда входной сигнал идентичен своему весовому вектору .

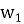
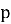
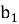
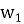
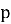
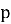
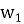
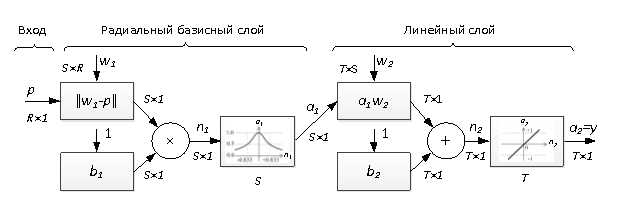
Рис. 1. Архитектура радиальной базисной нейронной сети

Смещение регулирует при обучении нейронной сети распространение радиального базисного нейрона. Например, если бы нейрон имел смещение 0.1; то он выдал бы коэффициент распространения 0.5 для любого входного вектора на векторном расстоянии 8.326 из его вектора весов [5].

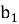
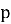
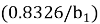
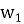
Выходной сигнал нейронов скрытого слоя рассчитывается по формуле (1), а результирующий сигнал сети по формуле (2).

(1)

(2)

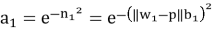
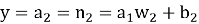
Проектируемая нейронная сеть будет иметь два входа и один выход, соответствующие количеству параметров исходных данных. Согласно архитектуре сети для ее работы подготавливается размерность входных и выходных данных. Координатная сетка логарифмического временного пространства двух параметров X и Y из матриц размером 20×21 преобразуется в одну входную матрицу P размерностью 2×420, используемую для обучения нейронной сети. Аналогичные преобразования выполняются для целевых, т. е. выходных данных T с размерностью 1×420 (рисунок 2).

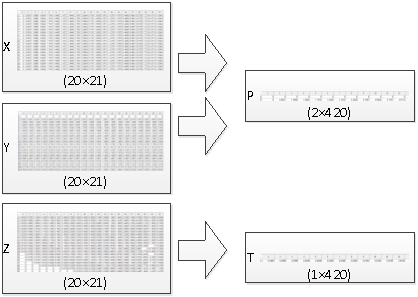
Рис. 2. Порядок подготовки исходных данных для нейронной сети

На этапе обучения нейронной сети каждой подготовленной паре из вектора исходных данных P ставится в соответствие целевые выходные данные из вектора T . Обучение сети продолжается в течение 400 эпох до достижения значения среднеквадратичной ошибки Perfomance меньше заданного целевого значения Goal, как показано на рисунке 3.

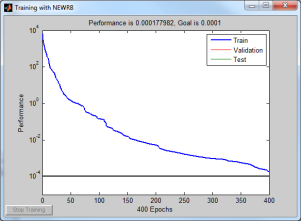
Рис. 3. График среднеквадратичной ошибки в зависимости от количества эпох при обучении нейронной сети

Обученная нейронная сеть формирует на выходе сигналы не только соответствующие фиксированным табличным данным, но и доступные во всем диапазоне областей определения значений входных величин.

Проверка адекватности аппроксимированных данных выполнена с помощью ранговой корреляции. Результаты проверки обоснованы двумя показателями — коэффициентом линейной корреляции r между парами значений двух сравниваемых векторов и p -значениями для проверки гипотезы об отсутствии корреляции с альтернативной гипотезой о ненулевой корреляции.

Минимальное значение коэффициента корреляции r между наборами сравниваемых данных имеет величину 0.6474, что представляет высокую положительную корреляцию между данными. Максимальное p -значение равно нулю с точностью до трех цифр. Поскольку p -значение меньше уровня значимости 0.05, это указывает на отклонение гипотезы об отсутствии корреляции между наборами данных.

Наглядное представление поверхностей доз излучений, построенных по табличным значениям и по результатам аппроксимации с использованием нейронной сети (показаны на рисунке 4), демонстрирует получение адекватных результатов.

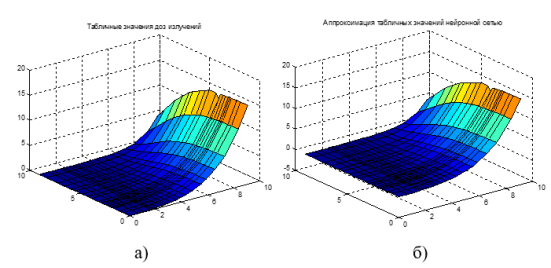
Рис. 4. Поверхности доз облучений, построенные по табличным значениям (а) и по результатам аппроксимации нейронной сетью (б)

Таким образом, применение технологий искусственного интеллекта для аппроксимации табличных данных доз облучения, получаемых населением (персоналом, личным составом) после аварии на радиационно опасном объекте при открытом расположении в середине зоны загрязнения, позволяет получить величину дозы для произвольного значения времени продолжительности пребывания в зоне загрязнения и времени начала излучения после аварии. Это позволит в ходе расчётов использовать значения (отсутствующие в табличных данных) продолжительности пребывания в зоне загрязнения и времени начала облучения после аварии, что существенно повысит точность и возможности по проведению расчётов.

Литература:

1. «Росатом» создает отраслевую систему мониторинга радиационной обстановки [Электронный ресурс]. — URL: https://strana-rosatom.ru/2022/06/24/rosatom-sozdaet-otraslevuju-sistem/ (дата обращения: 27.12.2023).
2. Единая государственная автоматизированная система мониторинга радиационной обстановки на территории Российской Федерации [Электронный ресурс]. — URL: http://egasmro.ru/ru/about/monitsys (дата обращения: 27.12.2023).
3. Выявление и оценка радиационной обстановки при авариях на атомных электростанциях. — Москва: Издание Военной ордена Октябрьской революции Краснознаменной Академии химической защиты им. Маршала Советского Союза С. К. Тимошенко, 1989. — 108 с.
4. Алексеев, Д. С. Технологии интеллектуального анализа данных: учебник для вузов / Д. С.Алексеев, О. В.Щекочихин. –2-е изд., стер. — Санкт-Петербург: Лань, 2024. — 176 с.: ил. — Текст: непосредственный. ISBN 978–5–507–48763–9
5. Demuth, H. Neural Network Toolbox User’s Guide / H. Demuth, M. Beale. — The MathWorks, Inc, 2004. — 846 p.