Введение

Данный веб-инструмент предоставляет интерактивную платформу для исследования и понимания принципов работы ключевых алгоритмов оптимизации, в частности, градиентного спуска. Пользователи могут в реальном времени наблюдать, как алгоритм исследует поверхность двумерных функций, шаг за шагом находя их минимумы. Интерактивность позволяет экспериментировать с различными функциями, начальными точками и параметрами алгоритма (такими как шаг обучения), что способствует глубокому освоению того, как эти методы работают, какие у них есть сложности и как они применяются на практике.

Для исследования алгоритмов оптимизации используются математические функции, которые можно представить в виде графика поверхности (в 2D или 3D). На этих поверхностях:

– Вертикальная ось ( ): представляет значение функции .

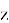
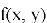
– Горизонтальные оси : представляют входные параметры, которые мы хотим оптимизировать.

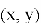
Основная цель оптимизации заключается в поиске точки на графике функции, где ее значение достигает минимума (или максимума). Максимумом (строгим) функции называется такое значение этой функции, которое больше всех ее значений , принимаемых данной функцией в точках некоторой окрестности точки . [1]

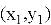
Градиент в любой точке поверхности указывает направление наибольшего ускорения роста функции. Алгоритмы оптимизации используют эту информацию, двигаясь в противоположном направлении (т. е. наискорейшего убывания), чтобы эффективно достичь минимума.

Изучение этих поверхностей позволяет понять, почему алгоритмы оптимизации работают именно так, и какие стратегии (например, выбор шага обучения, использование более продвинутых алгоритмов) помогают преодолевать их сложности.

Данная веб-страница предоставляет интерактивную платформу для исследования и понимания принципов работы численных методов оптимизации, в частности, градиентного спуска.

Интерфейс страницы предлагает следующий функционал: в центре внимания находится интерактивный трехмерный график, построенный с использованием библиотеки Plotly.js [4], который наглядно отображает поверхность выбранной двумерной математической функции . Пользователь имеет возможность выбрать одну из пяти предложенных тестовых функций, каждая из которых демонстрирует уникальные особенности ландшафта, влияющие на процесс оптимизации — от простой выпуклости до наличия множества локальных минимумов, узких долин или «плато» (рис. 1).

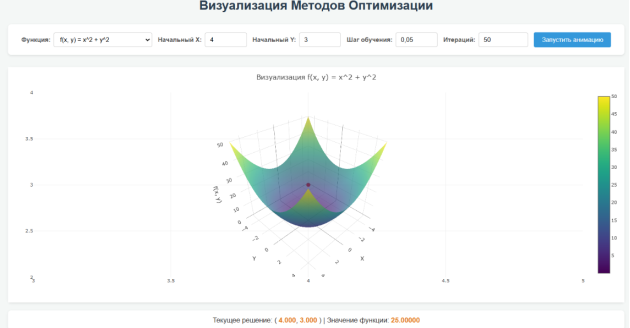
Рис. 1. Интерфейс страницы визуализации

Для управления процессом поиска минимума доступны следующие настройки: можно задать начальную точку , с которой начнется поиск, а также отрегулировать шаг обучения ( ) — параметр, контролирующий размер каждого шага алгоритма в направлении антиградиента. Также определяется общее количество итераций ( ), которое задает продолжительность работы алгоритма.

При нажатии на кнопку «Запустить анимацию» начинается выполнение алгоритма. В режиме реального времени на графике отображается траектория движения точки, представляющей текущее решение. Параллельно с этим, в каждой точке траектории визуализируется вектор градиента, указывающий направление наискорейшего роста функции, а алгоритм, в свою очередь, движется строго в противоположном направлении. После завершения анимации или в процессе ее выполнения, в нижней части страницы отображаются текущие координаты найденного решения и соответствующее значение функции , позволяя оценить точность и качество результата.

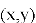
Принцип нахождения минимума. Основной принцип работы этого инструмента заключается в итеративном численном методе, известном как градиентный спуск. Он базируется на фундаментальном свойстве многомерных функций: вектор градиента в любой точке всегда указывает направление наискорейшего возрастания функции. Для того чтобы максимально быстро найти минимум, алгоритм следует в направлении, прямо противоположном вектору градиента, то есть в направлении антиградиента .

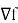
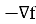
Этот процесс описывается итеративной формулой: . Здесь представляет текущее решение улучшенное решение на следующей итерации шаг обучения положительное скалярное значение контролирующее длину каждого шага, а вектор градиента функции точке .

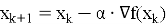
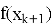
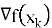
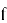
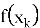
Процесс начинается с выбора начальной точки и задания параметров и . Затем, на каждой итерации , вычисляется градиент, и точка перемещается по поверхности в направлении антиградиента. Алгоритм останавливается либо по достижении заданного числа итераций , либо когда градиент становится пренебрежимо малым, что свидетельствует о достижении минимума функции. Таким образом, градиентный спуск является итеративным методом, который, используя локальную информацию о наклоне поверхности, методично приближается к ближайшему минимуму.

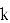
Для наглядной демонстрации работы алгоритмов оптимизации и исследования их поведения в различных условиях был выбран набор из пяти двумерных функций, каждая из которых обладает уникальными характеристиками, позволяющими проиллюстрировать ключевые аспекты, сложности и возможности методов поиска минимумов (рис. 2).

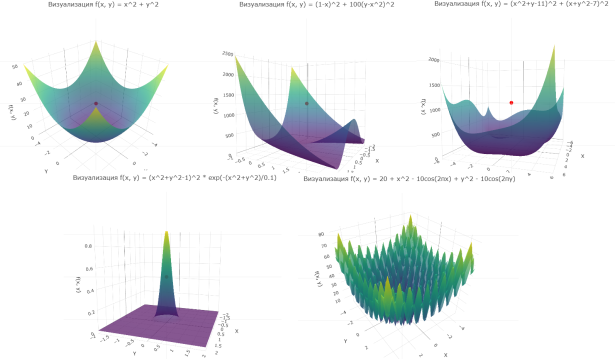
Рис. 2. Используемые функции

Квадратичная функция, , является простейшей выпуклой функцией с единственным глобальным минимумом в точке . Ее гладкий параболоидный график делает ее идеальной для понимания базового принципа работы градиентного спуска: как алгоритм быстро и надежно сходится к минимуму при правильном выборе шага обучения.

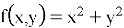
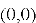
Функция Розенброка [2], . Она имеет один глобальный минимум в точке , но характеризуется узкой, изогнутой долиной, ведущей к нему. Эта функция позволяет исследовать сложности, связанные с медленной сходимостью вдоль таких долин или риском «перескочить» минимум при слишком большом шаге обучения.

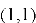
Функция Химмельблау, , интересна тем, что обладает четырьмя локальными минимумами. Это наглядно демонстрирует проблему локальных оптимумов: в зависимости от начальной точки, градиентный спуск может сойтись к любому из этих минимумов, не достигнув глобального.

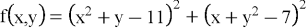
Функция «Мексиканская шляпа», , имеет один локальный минимум в центре и окружность из глобальных минимумов на радиусе . Ее выбор позволяет изучить поведение алгоритмов в областях с нулевым градиентом, которые не являются ни минимумами, ни максимумами, а также рассмотреть сценарий с «ожерельем» минимумов.

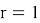
Наконец, функция Растригина [3], , представляет собой одну из самых сложных задач для тестирования алгоритмов глобальной оптимизации. Она обладает множеством локальных минимумов, расположенных по всей области определения, и один глобальный минимум в точке . Эта функция ярко иллюстрирует крайнюю степень проблемы локальных минимумов и высокую чувствительность к шагу обучения, подчеркивая, почему простые градиентные методы могут «застревать», и демонстрируя необходимость более совершенных подходов для поиска глобального оптимума.

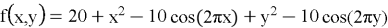
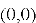
В совокупности, эти функции позволяют глубоко понять как базовые принципы работы градиентного спуска, так и распространенные сложности, с которыми сталкиваются при решении реальных задач оптимизации в различных областях, включая машинное обучение, инженерное проектирование и научные исследования.

Полный код для визуализации представлен в [5].

Выводы

В рамках проделанной работы был разработан интерактивный веб-инструмент на JavaScript, использующий библиотеку Plotly.js, для визуализации работы алгоритмов оптимизации, в частности, градиентного спуска. Инструмент позволяет пользователям исследовать поведение алгоритма на пяти различных двумерных функциях, каждая из которых выбрана для иллюстрации специфических аспектов оптимизации: от простого поиска единственного минимума до решения задач с множеством локальных минимумов, узкими долинами и особенностями поверхности. Пользователи могут настраивать параметры алгоритма, такие как начальная точка и шаг обучения, а также наблюдать за процессом поиска минимума в реальном времени, включая траекторию движения точки и вектор градиента. Данная визуализация значительно упрощает понимание принципов работы численных методов оптимизации, их сильных и слабых сторон, что критически важно для применения этих методов в таких областях, как машинное обучение, инженерия и научные исследования.

Литература:

1. Демидович Б. П. Краткий курс высшей математики: учеб. пособие для вузов / Б. П. Демидович, В. А. Кудрявцев. М.: Астрель, 2001. — 656 с.
2. Rosenbrock, H. H. (1960), An automatic method for finding the greatest or least value of a function, The Computer Journal, 3: p. 175–184.
3. Rastrigin, L. A. «Systems of extremal control». Mir, Moscow (1974).
4. [Электронный ресурс]. URL: https://cdn.plot.ly/plotly-2.27.0.min.js (дата обращения: 21.10.2025).
5. [Электронный ресурс]. URL: https://codepen.io/Ilona-Vlasenko/pen/OPMzzXB (дата обращения: 21.10.2025).