Введение

Классическая термодинамика и классическая статистическая механика хорошо описывают макроскопические процессы в термическом равновесии, но оказываются недостаточными для описания высокоэффективных, окончательно нерегулируемых и неравновесных процессов на масштабе молекул и белковых комплексов. Экспериментальные данные по переносу возбуждения в светособирающих комплексах показывают наличие продолжающихся квантовых когерентных осцилляций в течение времен, сопоставимых с временами переноса энергии, что ставит под вопрос грубое представление о мгновенной декогеренции в «теплой и влажной» среде. Эти наблюдения породили программу применения теории открытых квантовых систем и соответствующей квантовой термодинамики для биологических задач [1].

Одновременно теоретические исследования выявили механизм «помощи среды» — когда определенный уровень флуктуаций среды повышает эффективность переноса энергии (ENAQT) — и его связь с классическими механизмами, а также важность учета вибраций и структурированной спектральной плотности среды для адекватного моделирования реальных молекулярных комплексов [2, 3, 4].

Постановка задачи. Модель системы и среды

Рассматриваем подсистему (например, электронные уровни хромофора или двухуровневая система «донор–акцептор») и окружающую среду (белковая матрица, фононы, вода).

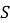
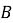
Полная гамильтониана:

.

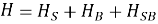
Типичные составляющие:

— гамильтониан подсистемы (двухуровневый или многосайтовый модель), содержащий межсайтовые переходы и локальные энергозоны;

— модель бани фононов (многочисленные моды среды);

— оператор взаимодействия (в простейшей спин-бозонной версии и ).

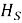
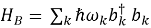
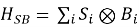
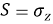
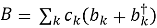
Основная задача — получить уравнение движения для редуцированной матрицы плотности и через нее вычислить динамику популяций, когерентностей и термодинамические величины.

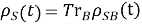
Уравнения динамики: марковский и немарковский подходы

1. Марковская редукция и форма Линблада

В случае слабой связи с большой памятью-короротермальной средой и при выполнении приближения Бора–Маркова, эволюция описывается уравнением в форме Линблада:

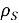
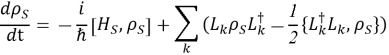
где — операторы релаксации и декогеренции. Такая форма гарантирует полную позитивность и сохранение вероятности и служит базисом для большинства теоретических выкладок и расчетов в термодинамике открытых систем [9, 10].

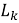
2. Немарковские эффекты и структурированная среда

При сильной связи, при наличии резонансных вибрационных мод или, когда спектральная плотность среды несглаженная / сильно структурирована, применяется немарковский формализм: временно-сверточные и безвременные генераторы, и/или численные подходы, а также вычисление спектральной плотности на основе классической молекулярной динамики и квантовой коррекции. Важность точной спектральной плотности для правильного предсказания релаксаций, декогеренции и спектров подчеркнута в ряде современных исследований [6].

Модель спин-бозона и расширения (электрон-вибрационная корреляция)

Базовая модель спин-бозона для двухуровневой системы:

.

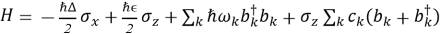
Эта модель описывает конкуренцию когерентного туннелирования ( ) и релаксации, обусловленной средой. Для реальных биомолекул модель расширяют включением:

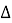
— дискретных сильных вибрационных мод (вибронов), связанных с локальными структурами;

— многосайтовой структуры (сеть хромофоров), где перенос определяется как комбинация локальных переходов и кооперативных эффектов;

— коррелированных шумов (временных и пространственных корреляций) и конформационной динамики белка.

Такие расширения необходимы для описания сложного взаимодействия VAET и шум-ассистированного переноса ENAQT, а также для разумного сравнения с экспериментальными данными [4, 2, 5].

Когерентность, шум и оптимальность переноса энергии

1. Конструктивная роль шума

Классическая интуиция о том, что шум неизбежно разрушает квантовую когерентность, изменилась: умеренный шум способен разрушить локализацию и тем самым открыть более эффективные траектории переноса — основной механизм ENAQT. При слишком слабом шуме локализация на дисперсных состояниях снижает перенос; при слишком сильном шуме возникает квантовый «Зено-эффект» — подавление переноса [2, 3].

2. Взаимодействие VAET и ENAQT

Если в системе присутствуют выраженные локальные вибрации, они могут резонансно усиливать перенос (VAET). Механизм VAET и ENAQT могут конкурировать или усиливать друг друга в зависимости от спектральной структуры среды и уровня шума: в слабом классе шума VAET доминирует, но при увеличении шума воспроизводятся типичные черты ENAQT, включая поворот в режим Зено-подавления при очень сильном шуме [4].

3. Множественные оптимумы и влияние неоднородности

Недавние теоретические исследования показали, что в неоднородных и разреженных сетях переноса могут существовать не один, а несколько оптимальных режимов диссипации — «двойные пики» эффективности переноса. Это означает, что понятие «золотой середины» шума расширяется: геометрия сети и распределение локальных параметров порождают сложную карту оптимальности шума [5].

Квантово-термодинамические величины: определение и вычисление

1. Энтропия фон Неймана

Для подсистемы вводим энтропию фон Неймана:

.

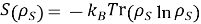
Изменение отражает изменение смешанности состояния и является отправной точкой для оценки необратимости.

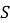
2. Тепловые потоки и работа

Разделение изменения энергии подсистемы на тепло и работу определяется стандартной квантово-термодинамической схемой:

,

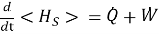
где

, .

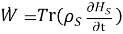
В случае стационарного гамильтониана работа от внешних полей равна нулю и все изменение энергии связано с тепловыми потоками и переносом в другие подсистемы.

3. Производство энтропии

Производство энтропии для подсистемы можно записать как

,

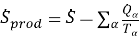
где суммирование производится по резервуарам с температурой . В квантовом случае корректный подсчет требует аккуратного выделения вкладов диссипатора и учета взаимодействия с окружением, особенно в немарковских ситуациях, когда возможен обратный перенос энергии и информации [9, 6].

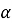
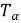
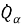
4. КПД и «полезная» энергия

Для фотосинтетических систем полезная энергия определяется как энергия, доставленная в реакционный центр за время до рекомбинации. Квантовый КПД:

,

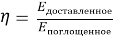
и на практике зависит от скорости переноса, уровней потерь (релаксация в невосстановительные каналы) и от параметров среды.

Практические расчеты и численные подходы

Для реальных молекул требуется сочетание методов: QM/MM для получения параметров , молекулярная динамика для автокорреляционных функций и спектральной плотности среды, HEOM или другие немарковские алгоритмы для точного интегрирования динамики. Для больших систем применяются приближенные мастер-уравнения с подстройкой диссипатора под вычисленную спектральную плотность. В последние годы также исследуются возможности квантовой симуляции открытой динамики как инструмент проверки моделей [6, 13].

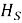
Физические результаты и их значение для биологических систем

1. Шум как ресурс. При умеренном уровне взаимодействия с окружением когерентность и диссипация балансируют так, что достигается повышенная вероятность упорядоченного переноса энергии. Это дает объяснение высокой эффективности в светособирающих комплексах при физиологических температурах [2, 3].
2. Вибрации среды — не мелочь. Наличие сильных локальных вибрационных мод и структурированной спектральной плотности изменяет картину переноса: возможны резонансные усиления передачи и изменение оптимальных условий шума [4, 6].
3. Неоднородность дает новые режимы. В сложных сетях переноса (биологические антенны с неоднородными параметрами) может возникать несколько оптимальных режимов диссипации — это дает более широкую «устойчивость» эффективности к вариациям внешних условий [5].
4. Термодинамика информации. Когерентность и квантовые корреляции влияют на энтропийные потоки и тем самым на эффективное производство энтропии; это поднимает вопрос о роли квантовой информации в биологических процессах и в уточненной формулировке второго начала для открытых квантовых систем [9, 7].

Рекомендации для моделирования и экспериментов

Всегда сопоставлять модельную спектральную плотность с данными MD/эксперимента: белый шум — слишком грубое приближение. Для многих задач необходима структурированная спектральная плотность. Практическая рекомендация — вычислить автокорреляцию флюктуаций гамильтониана и преобразовать ее в спектральную плотность [6].

При поиске оптимального режима шума учитывать структуру сети: сканировать силу связи с термостатом и характеристики вибраций, и искать возможные несколько локальных максимумов эффективности [5].

Для сравнения с экспериментом измерения фемто- и пикосекундной спектроскопии должны сопровождаться моделированием немарковских эффектов; однозначные выводы о функциональной роли когерентности требуют моделирования и анализа энтропийных потоков, а не только наблюдения бит-осцилляций [1, 4].

Разработка квантовых симуляторов и алгоритмов для открытых систем — перспективное направление для тестирования гипотез о роли шума и вибраций в биологических комплексах [13].

Заключение

Термодинамика открытых квантовых систем предоставляет последовательный и вычислительно реализуемый аппарат для моделирования ключевых биологических процессов на молекулярном уровне. Учет структурированной среды, вибраций и возможной немарковской динамики позволяет перейти от качественных сценариев к количественным прогнозам эффективности переноса энергии, производства энтропии и роли квантовой когерентности. Современные исследования демонстрируют, что шум и фононная среда могут быть не только источником потерь, но и ресурсом, который биологические системы, возможно, эволюционно используют для повышения КПД при физиологических условиях.

Литература:

1. Engel G. S., Calhoun T. R., Read E. L., Ahn T.-K., Mancal T., Cheng Y.-C., Blankenship R. E., Fleming G. R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems // Nature. — 2007. — Vol. 446. — P. 782–786.

2. Rebentrost P., Mohseni M., Kassal I., Lloyd S., Aspuru-Guzik A. Environment-assisted quantum transport // New J. Phys. — 2009. — Vol. 11. — 033003.

3. Plenio M. B., Huelga S. F. Dephasing-assisted transport: quantum networks and biomolecules // New J. Phys. — 2008. — Vol. 10. — 113019.

4. Li Z.-Z., Ko L., Yang Z., Sarovar M., Whaley K. B. Interplay of vibration- and environment-assisted energy transfer. arXiv:2110.09895 (2021). DOI/URL: https://arxiv.org/abs/2110.09895.

5. Coates A. R., Lovett B. W., Gauger E. M. From Goldilocks to Twin Peaks: multiple optimal regimes for quantum transport in disordered networks. arXiv:2210.11875 (2022). DOI/URL: https://arxiv.org/abs/2210.11875.

6. Holtkamp Y. M., Godinez-Ramirez E., Kleinekathöfer U. Spectral densities, structured noise and ensemble averaging within open quantum dynamics // J. Chem. Phys. — 2024. — Vol. 161. — 134101. DOI/URL: https://doi.org/10.1063/5.0224807.

7. Aleksashin M. K., Basharov A. M., Trubilko A. I. A local approach to the theory of open optical quantum systems and “violation” of the second law of thermodynamics // Izvestiya Rossiiskoi Akademii Nauk. Seriya Fizicheskaya. — 2023. — Vol. 87, No. 10. — P. 1482–1492. DOI: 10.31857/S0367676523702599.

8. Сюракшин А. В., Салеев В. А., Юшанхай В. Ю. Квантовые модели в биологии // Вестник Самарского университета. Естественнонаучная серия. — 2022. — Т. 28, № 1–2. — С. 74–94. URL: https://journals.ssau.ru/est/article/view/10972.

9. Breuer H.-P., Petruccione F. The Theory of Open Quantum Systems. — Oxford: Oxford University Press, 2002.

10. Lindblad G. On the generators of quantum dynamical semigroups // Commun. Math. Phys. — 1976. — Vol. 48. — P. 119–130.

11. Weiss U. Quantum Dissipative Systems. 4th ed. — Singapore: World Scientific, 2012.

12. Kim Y. Quantum biology: an update and perspective // Quantum Rep. (MDPI) — 2021. URL: https://www.mdpi.com/.

13. Quantum algorithm for solving open-system dynamics on quantum computers using noise // Phys. Rev. A. — 2023. — Vol. 108. — 062424. DOI/URL: https://doi.org/10.1103/PhysRevA.108.062424.