В статье проведена классификация задач на суммирование дискретных функций по содержанию и по способу их решения.

Ключевые слова: дискретная функция, классификация, задача суммирования дискретных функций.

Известно, что классификация является одним из разновидностей мысленного деления предметов на группы. Чтобы провести классификацию необходимо определить ее основание, т. е. признак по которому мы будем различать эти предметы. В данном случае мы будем классифицировать задачи на суммирование дискретных функций.

Если за основание классификации данных задач взять содержание , то их можно делить на следующие группы:

1. задачи с абстрактно-математическим содержанием;
2. задачи с реально-практическим содержанием;
3. задачи с историческим содержанием.

При решении задач второй группы используется метод математического моделирования, который состоит из следующих этапов:

а) этап математического моделирования;

б) исследование математической модели и формулировка результата;

в) этап интерпретации полученного результата.

При решении задач с абстрактно-математическим содержанием используется только второй этап. Задачи с историческим содержанием — это задачи, условия которых отражают факты из истории развития математики.

Примеры задач абстрактно-математического содержания:

Задача № 1. Найдите сумму

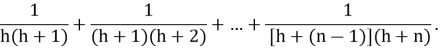
Решение. Для удобства запишем данную сумму с помощью оператора суммы. Тогда, бесспорно, она примет следующий вид:

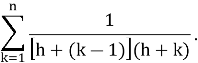
Как известно для того чтобы вычислить сумму надо найти такую функцию натурального аргумента, разность которой бы равнялась функции, находящейся под знаком суммы. Другими словами, по данной разности надо восстановить В нашем частном случае данная разность

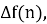
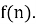
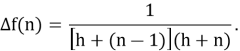
Найдем функцию с помощью метода неопределенных коэффициентов:

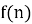
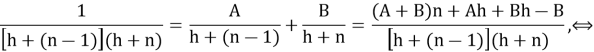
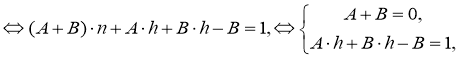
Решая последнюю систему, получаем Следовательно,

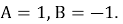
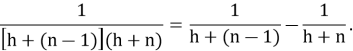
Из последнего равенства становится ясно, что:

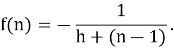
В самом деле, — искомая функция, т. к.:

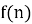
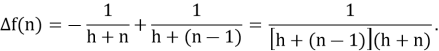
Наконец, по формуле (1.2–2) мы находим нашу сумму:

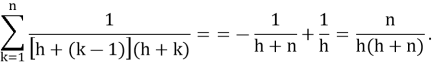
Задача № 2. На плоскости расположены две касающиеся друг друга внешним образом окружности единичного радиуса. К ним проведена внешняя касательная. В фигуру, заключенную между окружностями и касательной, вписывается круг, затем в образовавшуюся фигуру между данными окружностями и первым кругом вписывается второй круг и т. д. Спрашивается, какова суммарная длина диаметров вписанных кругов, полученных на м шаге.

Пример задачи на суммирование с реально-практическим содержанием:

Задача № 3. Как известно, клетки размножаются делением. Одноклеточная зеленая водоросль Chlorogonium, которая встречается в прудах и реках, имеет форму эллипса. Обычно она достигает размеров, превышающих исходные приблизительно в 4 раза, а затем делится на 4 дочерние клетки. Сколько водорослей образуется после делений 100 таких растений?

Решение: Известно, что одна водоросль делится на 4 дочерние. По условию задачи одновременно делится 100 одноклеточных зеленых водорослей. Следовательно, после первого деления число растений станет равным 400. После второго — 1600 и т. д.:

100, 400, 1600, 6400, … (*)

Нетрудно видеть, что (*) — геометрическая прогрессия с первым членом и знаменателем Следовательно, искомая сумма будет равна:

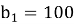
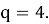
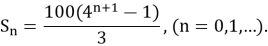
Пример задачи на суммирование функций с историческим содержанием:

Задача № 4. Китайский ученый Шэнь Ко (11 в.) в своем сочинении «Рассуждения Мэн-си» приводит такую задачу: вычислить число предметов, образующих слойную ступенчатую усеченную пирамиду, в которой стороны прямоугольных слоев последовательно увеличиваются на единицу. Если известно, что в наименьшем слое предметов.

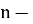
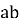
Вычислите следующую сумму, к которой сводилось решение выше приведенной задачи Шэнь Ко:

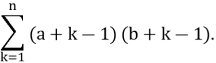
Решение: Раскрывая скобки выражения, находящегося под знаком суммы и проводя группировку слагаемых, получаем:

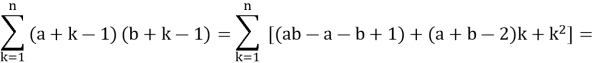
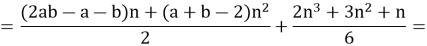
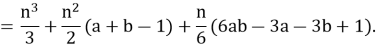
Если способ решения — основание классификации наших задач, то можно выделить следующие группы:

1. арифметические;
2. алгебраические (составление уравнений, неравенств и т. п.);
3. геометрические (через использование геом-х фигур и их свойств);
4. комбинированные;

Примеры арифметически решаемых задач на суммирование функций:

Задача № 5. Вычислить сумму

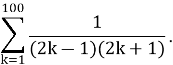
Задача № 6. Доказать справедливость равенства

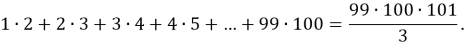
Нетрудно догадаться, что в задачах № 5 и № 6 речь идет о сложении ста чисел.

Пример задачи суммирования решаемой алгебраически:

Задача № 7. Найдите сумму:

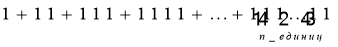
Решение: Запишем данную сумму в виде

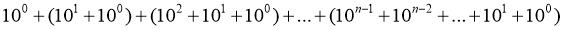
Нетрудно, догадаться, что слагаемые последней суммы можно сгруппировать и представить сумму в более удобной для вычисления форме:

.

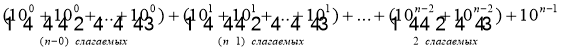
После вычисления сумм слагаемых в каждой скобке, искомая сумма примет вид

.

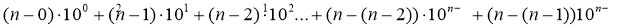
Из последнего выражения становится очевидным закономерность, т. е. формула члена, зная которую нашу сумму можно написать в более компактной форме

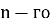
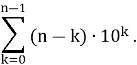
Понятно, что вычислять последнюю сумму надо с помощью метода частичного суммирования, с которым мы познакомились в 1.2, т. е. надо воспользоваться формулой (1.2–3). Для этого представим последнюю сумму в виде:

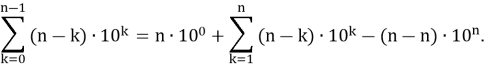
Легко видеть, что вычитаемое в правой части последнего тождества равна нулю. Следовательно, равенство окончательно примет вид:

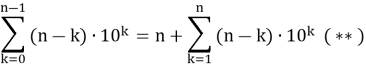
Для вычисления второго слагаемого в правой части равенства прибегнем к преобразованию Абеля, т. е. к методу частичного суммирования. Значит, положив получим

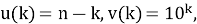
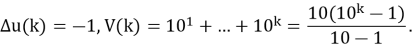
Подставляя в формулу (1.2–3), полученные выражения и, проводя необходимые промежуточные вычисления, получаем:

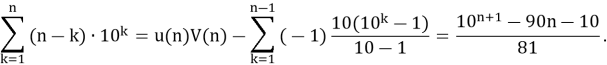
Теперь подставляя вычисленное значение последней суммы в равенство (**) получаем искомое выражение для исходной суммы, а именно:

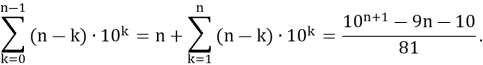
Таким образом, мы вычислили сумму

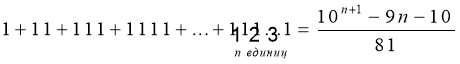
Примеры задачи суммирования функций решаемых геометрически:

Задача № 8. Длина стороны равностороннего треугольника равна а. На его высоте, как на стороне, построен новый равносторонний треугольник. На высоте нового треугольника, как на стороне, построен еще один равносторонний треугольник. И т. д. Найдите сумму периметров и сумму площадей всех таких треугольников.

Решение. Обозначим сторону исходного равностороннего треугольника, данного нам по условию, через т. е. Зная сторону, мы можем найти все его элементы. В частности, высота будет равна

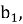
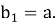
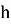
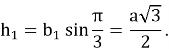
Известно, что сторона второго равностороннего треугольника равна высоте первого:

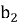
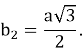
Тогда легко можно вычислить высоту второго равностороннего треугольника:

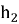
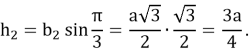
По условию третий равносторонний треугольник постороен на высоте как на стороне. Значит, сторона третьего треугольника равна

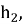
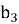
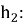
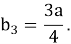
Схожим образом, находятся стороны остальных равносторонних треугольников, построенных на высотах предыдущих треугольников, как на сторонах.

Продолжая этот процесс, получим последовательность длин сторон правильных треугольников:

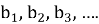
Любой член этой последовательности — сторона равностороннего треугольника, высотой которой является следующий член последовательности: сторона треугольника высота которого сторона треугольника высота которого и т. д. (Рис. 1).

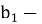
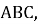
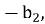
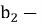
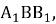
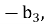
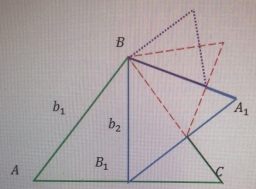
Рис. 1

Высота правильного треугольника вычисляется умножением стороны на

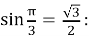
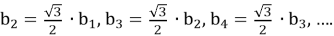
Таким образом, полученная выше последовательность сторон

правильных треугольников геометрическая прогрессия.

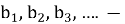
Обозначим периметр го треугольника через Тогда искомая сумма периметров будет равна:

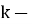
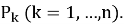
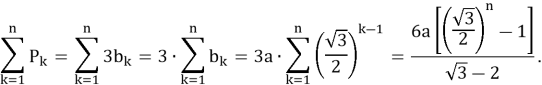
Аналогично, вычисляется сумма площадей всех таких треугольников. Если обозначить через площадь го треугольника , то

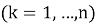
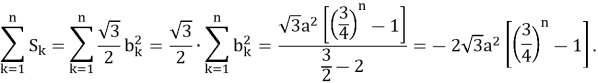
Задача № 9. Вравносторонний треугольник с длиной стороны а вписана окружность. В эту окружность вписан новый равносторонний треугольник. В этот треугольник опять вписана окружность, а в окружность -- еще равносторонний треугольник. И т. д. Найдите сумму длин всех таких окружностей и сумму площадей всех таких кругов.

Из условия ясно, что для решения этой задачи необходимо рассматривать свойства таких геометрических фигур как окружность, треугольник и круг (Рис. 2).

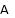
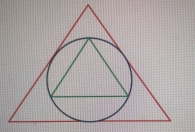
Рис. 2.

Литература:

1. Алфутова Н. Б. Устинов А. В. Алгебра и теория чисел. Сборник задач для математических школ. 3-е изд., испр. и доп. — М.: МЦНМО, 2009. — 336 с.
2. Гашков С. Б. Современная элементарная алгебра в задачах и решениях. — М.: МЦНМО, 2006. — 328 с.
3. Галкин Е. В. Нестандартные задачи по математике. Алгебра: Учеб. пособие для учащихся 7–11 кл. — Челябинск: «Взгляд», 2004. — 448 с.
4. Давидович Б. М., Пушкарь П. Е., Чеканов Ю. В. Математический анализ в 57-й школе. Четырехгодичный курс. — М.: МЦНМО, 2008. —176 с.
5. Сергеев П. В. Математика в спецклассах 57-й школы. Математический анализ. — М.: МЦНМО, 2008. — 159 с.