В статье автор исследует понятие методической схемы и формулирует основополагающие базовые принципы методической схемы индивидуализированного обучения в средней школе.
Ключевые слова: методическая схема, индивидуализированное обучение, методическая схема индивидуализированного обучения.
В научно-методической литературе можно встретить такие термины как «методическая схема изучения функции», «методическая схема обучения решению математических задач», «методическая схема урока», «методическая схема управления поиском решения задачи», «методическая схема введения понятия», «методическая схема приведения контрпримеров», «методическая схема применения абстрактно-дедуктивного метода введения понятия» и т. п. Анализ каждого из этих понятий приводит к пониманию того, что каждый из перечисленных выше терминов суть обобщенное поэтапное представление какого-либо процесса (изучения функции, введения понятия, урока и т. п.). Например, Ю. М. Колягин рекомендует изучение конкретной функции в основной школе проводить по методической схеме, которая представлена в таблице 3. Понятно, что в основной школе по этой схеме можно изучить и линейную, и квадратичную, и дробно-рациональную функцию и функцию
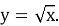
Таблица 1
Методическая схема изучения функции
|
№ |
Этап |
Характеристика этапа |
|
|
Рассмотреть конкретные примеры, практические задачи, которые приводят к данной (линейной, квадратичной, степенной и т. п.) функции |
Цель этого этапа — убедить обучающихся необходимости изучения данной функции в силу ее практической или теоретической значимости. |
|
|
Сформулировать определение данной функции |
Цель данного этапа — сформировать у обучающихся четкое представление о данной функции, о ее записи формулой, свойствах. |
|
|
Ознакомить с графиком данной функции |
На этом этапе обучающиеся научатся строить график данной функции, отличать ее график от графиков других функций, начнут понимать влияние параметров в формуле данной функции на ее график. |
|
|
Исследовать основные свойства данной функции |
Установление основных свойств данной функции (область определения, область значений, монотонность, промежутки знакопостоянства, нули, четность, нечетность и т. д.). |
|
|
Использовать изученные свойства данной функции при решении задач. |
Этот этап нацелен на закрепление основных понятий и теоретических положений, связанных с изучаемой функцией. |
Таким образом, выше приведенная методическая схема изучения функции — это обобщенный поэтапно представленный процесс изучения функций курса математики основной школы.
Рассмотрим еще один пример методической схемы. В таблице 4 представлена методическая схема приведения контрпримеров, которую рекомендует применять в процессе изучения конкретного понятия Н. М. Рогановский.
Таблица 2
Методическая схема приведения контрпримеров
|
№ |
Этап |
Пример 1 |
Пример 2 |
|
|
Сформулировать определение понятия |
Сформулировать определение многочлена |
Сформулировать определение трапеции |
|
|
Привести одновременно примеры и контрпримеры понятия |
Написать на доске список выражений, среди которых есть многочлены и немногочлены |
Представить вниманию обучающихся рисунки трапеций и нетрапеций |
|
|
Выяснить какие из них являются примерами, а какие — контрпримерами данного понятия |
Выяснить какие выражения являются многочленами, а какие — немногочленами |
Выяснить на каких рисунках изображены трапеции, а на каких нетрапеции |
Заметим, что в методической схеме не конкретизированы ни цель, ни содержание, ни методы, ни формы организации деятельности, ни средства, ни планируемые результаты, нет временных рамок и т. д. Этим она и отличается от таких понятий как план, программа, методическая система. Поясним сказанное на примерах.
Пример 1. Методическая схема изучения функции может быть применена и при изучении конкретной функции в общеобразовательном классе, и при изучении этой же функции в классе физико-математического профиля. Понятно, что, несмотря на изучение по одной и той же схеме, в классе с физико-математическим профилем круг изучаемых понятий и методов, связанных с изучаемой функцией будет значительно шире, времени будет выделено на изучение этой функции больше, планируемые результаты тоже будут отличаться.
Пример 2. Методическая схема изучения функции может быть применена и при изучении линейной функции, и при изучении квадратичной функции. Но при одной и той же схеме содержание обучения, например, будет разным: в первом случае содержание обучения — это линейная функция и круг понятий и методов, которые с ней связаны, а во втором — это квадратичная функция и круг понятий и методов, которые связаны с ней.
Итак, методическая схема — это обобщенное поэтапное представление конкретного процесса (изучения понятия, обучения, урока и т. п.).
Методическая схема обучения — это поэтапное представление процесса обучения. Этапы методической схемы обучения строго упорядочены, логически последовательны. Можно сказать, что методическая схема это своеобразный план (программа) обучения.
Методическая схема обучения задает ориентировочную основу педагогической деятельности и деятельности учения, оптимизирующую эту деятельность, технологичность которой задается структурированием и поэтапным представлением процесса обучения.
Начиная с 2015 году и по сегодняшний день обучающиеся средней школы сдают либо ЕГЭ по математике базового уровня, либо — профильного уровня[1]. На практике это привело к неформальному делению обучающихся одного класса средней школы на группы с разными образовательными потребностями: одним нужны глубокие знания по математике для успешной сдачи ЕГЭ профильного уровня и обучения в вузе, а другим — достаточны поверхностные знания для сдачи экзамена базового уровня на «4» или «5» и получения аттестата. Одним из направлений решения этой проблемы, которая заключается в обучении в одном классе обучающихся с принципиально разными образовательными потребностями, является разработка такой методической схемы обучения математике, которая обеспечивала бы учет их образовательных потребностей и других индивидуальных особенностей.
Цель статьи: сформулировать базовые принципы методической схемы индивидуализированного обучения.
На этапе проектирования методической схемы индивидуализированного обучения математике в средней школе с применением технологии смешанного обучения нами были сформулированы основополагающие, базовые принципы, которые обеспечили бы ее эффективность, открытость, функциональность и гибкость. Так в основу методической схемы индивидуализированного обучения математике в средней школе нами были заложены следующие базовые системообразующие принципы:
– принцип личностно-центрированного подхода;
– принцип дифференциации;
– принцип последовательности и систематичности;
– принцип доступности и наглядности;
– принцип практической направленности;
– принцип обратной связи.
В таблице 5 дано краткое описание всех выше сформулированных принципов и приведены примеры их реализации на практике.
Таблица 3
Описание принципов методической схемы обучения
|
Принцип |
Описание принципа |
Пример |
|
Принцип личностно-центрированного подхода |
Личностно-центрированный подход ставит в центр образовательного процесса личность ученика, его интересы, потребности и индивидуальные особенности. |
Регулярное обсуждение с обучающимся его успехов и неудач, предоставление индивидуальных рекомендаций по улучшению результатов. |
|
Принцип дифференциации |
Предполагает разделение обучающихся на группы согласно их уровню подготовки, образовательным потребностям и другим индивидуальным особенностям | |
|
Принцип последовательности и систематичности |
Обучение должно строится на основе логической последовательности и системности, чтобы знания и навыки формировались постепенно и последовательно, чтобы избежать пробелов в ЗУН и способствует глубокому пониманию материала. |
Темы вводятся последовательно, обеспечивая постепенное углубление знаний. |
|
Принцип доступности и наглядности |
Учебный материал должен подаваться в доступной и наглядной форме, используя схемы, диаграммы, графики, системы динамической математики и другие средства наглядности. |
Использование систем динамической математики при изучении стереометрии делает материал наглядным. |
|
Принцип практической направленности |
Обучение должно быть направлено на применение ЗУН в реальной жизни. Это делает обучение более наглядным, осмысленным и мотивирующим. |
Решение тригонометрических задач с практическим содержанием. |
|
Принцип обратной связи |
Регулярная оценка успехов и неудач обучающихся и обратная связь в виде индивидуальных рекомендаций позволяет корректировать учебный процесс, стимулировать и поддерживать мотивацию. |
Регулярный текущий контроль знаний обучающихся по математике. |
Литература:
- Методика преподавания математики в средней школе. Частные методики. Учебное пособие для студентов физ.-мат. фак. пед. институтов. / Ю. М. Колягин, Г. Л. Луканкин, Е. Л. Мокрушин [и др.]. — Москва: Просвещение, 1977. — 480 c.
- Рогановский, Н. М. Методика преподавания математики в средней школе: в 2 частях. — Часть 1: Общие основы методики преподавания математики (общая методика) / Н. М. Рогановский, Е. Н. Рогановская. — Могилев: УО «МГУ им А. А. Кулешова», 2010. — 312 c.
- Табанов, И. А. Об одном примере упражнения на опровержение ложных математических рассуждений / И. А. Табанов. — Текст: непосредственный // Молодой ученый. — 2020. — № 20 (310). — С. 8–11. — URL: https://moluch.ru/archive/310/69946/
[1]Концепция новой модели ЕГЭ по математике, которую предложили на Всероссийском общественном обсуждении вопросов совершенствования государственной итоговой аттестации (ГИА), которое прошло 26-30 августа 2024 года, меняет только форму организации ЕГЭ по математике — экзамены базового и профильного уровня будут объединены. А по сути, новый ЕГЭ по математике будет состоять из двух частей. Первая часть будет состоять из заданий базового уровня сложности, а вторая часть будет состоять из заданий повышенной сложности. Предполагается, что сдача первой части будет обязательным условием для выдачи аттестата, а вторую часть будут сдавать выпускники, которые планируют поступать в вузы, где требуется профильная математика. Поэтому сформулированная проблема останется актуальной и после внедрения новой модели ЕГЭ по математике.

