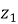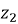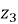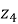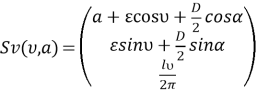В статье автор исследует возможность применения эксцентриково-циклоидального зацепления (далее также — ЭЦ-зацепление) разработчика В. В. Становского для цилиндрических, конических колес или в реечной передаче в качестве замены длительно используемому эвольвентному зацеплению, а также возможность применения перспективного технического решения в разработках конструкций новых видов передач с большим КПД и меньшими габаритными размерами.

Ключевые слова: эксцентриково-циклоидальное зацепление, эвольвентное зацепление, зубчатые передачи.

Массово применяемые в машиностроении редуктор и зубчатые колеса с эвольвентным зацеплением, несмотря на свои достоинства, не лишены критических недостатков в виде недостаточной несущей способности, первопричиной которой является фактор величины передаточного отношения для одной ступени с учетом размера зубьев. Если существует необходимость повысить нагрузочную способность передачи с эвольвентным зацеплением, то требуется увеличивать габариты зубчатых колес.

Ранее разработанное советским инженером М. Л. Новиковым эвольвентное зацепление обладало высоким КПД, но массового распространения в машиностроении не получило из-за слишком высоких требований к изменению межосевого расстояния на станках. Сегодня возможность производства деталей машин на высокоточных станках решает эту проблему.

Разработчик эксцентриково-циклоидального зацепления В. В. Становской в описании изобретения к патенту RU 2 416 748 C1 указывает, что «зубчатые профили данных передач обладают точкой контакта, способной перемещаться во время работы вдоль линии зацепления, будучи параллельной осям колес. В то же время у зубчатых колес выпуклые поверхности начальных головок зубьев взаимодействуют с вогнутыми поверхностями начальных ножек зубьев. Для этого профили в торцевом сечении очерчиваются дугами окружностей с кривизной разных знаков. Коэффициент торцевого перекрытия зацепления равен нулю или близок к нулю. Плавность работы достигается за счет осевого перекрытия, коэффициент которого выбирают больше единицы» [1, с. 1].

Главной особенностью эксцентриково-циклоидального зацепления является большая площадь контакта поверхности криволинейного зуба, при этом точки контакта визуально образуют сплошную винтообразную линию. Силовой контакт в торцевых участках осуществляется на половине оборота эксцентрика, вследствие чего коэффициент осевого перекрытия меньше аналогичного коэффициента эвольвентного зацепления и составляет 1/2. При проектировании передачи в системах автоматизированного проектирования инженеру-разработчику рекомендуется задавать коэффициент осевого перекрытия зубчатого колеса эксцентриково-циклоидального зацепления равным 1 при наклоне зубьев 36°. В перспективе указанное техническое решение может стать инновационным в конструировании разных элементов механизмов промышленного назначения.

Становской В. В. с разработчиками Казакявичюсом С. М., Ремневой Т. А., Кузнецовым В. М. указывает в описании изобретения к патенту RU 2 416 748 C1, что «винтовые зубья первого профиля в главном сечении могут быть полностью очерчены эксцентрично смещенными окружностями. Тогда зубья второго профиля в том же главном сечении будут очерчены участками пересекающихся циклоидальных кривых, сопрягающихся с зубьями первого колеса. Эти циклоидальные кривые представляют собой эквидистанты циклоид, повернутых относительно друг друга на угол, равный шагу циклоиды, деленному на число зубьев колеса» [1, с. 1].

Мы можем полагать, что модель ЭЦ-зацепления целесообразно применять в проектировании достаточно широкого спектра зубчатых передач, а не только в таких распространенных, как цилиндрические или конические. Конструкцию эксцентриково-циклоидального зацепления можно применять в проектировании специализированных реечных передач. Это показывает высокую перспективность эксцентриково-циклоидального зацепления не только в качестве замены длительно используемому эвольвентному зацеплению, но и как новое техническое решение для проектирования новых видов зубчатых передач с большим коэффициентом полезного действия и меньшими габаритными размерами.

В цилиндрических колесах основным критерием зацепления выступают главные торцевые сечения. В реечных передачах главным сечением выступает плоскость, перпендикулярная оси шестерни и параллельная рейке. В таблице 1 представлены параметры конструкции зубчатых колес для эвольвентного и эксцентриково-циклоидального зацепления. На рисунке 1 дана визуализация динамики движения конструкции зубчатых колес для эвольвентного и эксцентриково-циклоидального зацепления.

Таблица 1

Сравнение характеристик передач на эвольвентном зацеплении и на ЭЦ-зацеплении

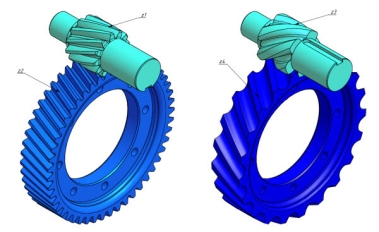
Рис. 1 Сравнение характеристик передач на эвольвентном зацеплении и на ЭЦ-зацеплении

Согласно исследованию инженеров Леонтьева М. Ю., Раевского В. А., Смоловик А. Е. [2] преимуществами зубчатых передач на основе ЭЦ-зацепления являются малые габаритные размеры при одновременной одинаковой нагрузочной способности поверхности соприкосновения зубьев колес (пятна контакта); высокий эксплуатационный ресурс и надежность, дающие постоянный КПД более 98 %; низкая виброактивность при работе на высоких скоростях; а также низкая себестоимость производства.

Перспективность широкого применения эксцентриково-циклоидального зацепления в качестве альтернативы эвольвентному зацеплению определяется возможностью при проектировании создать лучшее сцепление зубчатых колес и увеличить площадь пятна их контакта. Это позволит проектировать передачи с большим КПД, требующие от инженеров-конструкторов надежных и стабильно работающих производственных механизмов в условиях различных сценариев.

В исследовании «Математическое и компьютерное моделирование динамического состояния систем передачи движения» Н. Р. Щербаков предлагает математические расчеты проектирования элементов эксцентриково-циклоидального зацепления зубчатых передач в системах автоматизированного проектирования. «В отличие от эвольвентного зацепления, в котором профили зубьев изготовлены на основе эвольвенты окружности, в ЭЦ-зацеплении профили колес представлены циклоидальной кривой и эксцентрически повернутой окружностью» [3], что позволяет в конструировании понимать особенности вариаций нужных параметров зубчатого сцепления.

Филипенков А. Л., сравнивая несущую способность эксцентриково-циклоидального и эвольвентного зацепления, указывает, что «контакт поверхностей в ЭЦ-зацеплении есть контакт высших кинематических пар, поскольку имеет место несовпадение главных направлений контактирующих поверхностей» [4].

В построении цифровой модели эксцентриково-циклоидального зацепления в системах автоматизированного проектирования мы можем опираться на математические расчеты Н. Р. Щербакова. Визуализация пятна контакта, представленная на рисунках 2а и 2б, демонстрирует, что «ЭЦ-зацепление может быть реализовано как на составных колесах с повернутыми относительно друг друга прямозубыми венцами (рисунок 2а), так и в виде непрерывного винтового эксцентрика и сопряженного с ним винтового циклоидального колеса (рисунок 2б)» [3].

Рис. 2. Эксцентриково-циклоидальное зацепление: а) составные венцы; б) криволинейные винтовые зубья

Используя предложенную Н. Р. Щербаковым формулу расчета динамического состояния систем передачи движения на основе эксцентриково-циклоидального зацепления (1), мы можем проводить численный анализ параметров конструкции зубчатого колеса и определять поверхность винтового эксцентрика как «вектор-функцию двух аргументов υ и α, принимающих значения от 0 до 2π» [3]:

где υ — передаточное число;

α — угол наклона зубьев;

D — диаметр винтового эксцентрика;

ε — эксцентриситет (на рисунке 3 — это SO ₁ , где О ₁ — центр вращающейся оси; S — центр винтового эксцентрика; G — эквидистант эпитрохоиды);

l — длина винтового эксцентрика;

a — межцентровое расстояние колес (на рисунке 3 — это OS).

Филипенков А. Л. указывает, что «криволинейные зубья второго варианта передачи (рисунок 2б) обладают большим радиусом кривизны, это повышает контактную прочность зацепления, а форма зуба выдерживает более высокие нагрузки» [4], имея при этом вид, показанный на рисунке 3.

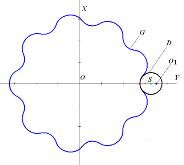
Рис. 3. Сечение ЭЦ-зацепления в модели Щербакова Н. Р.

Таким образом, рассмотренная автором возможность конструирования механизма передаточных отношений функций движения на принципе эксцентриково-циклоидального зацепления инновационной разработки российских инженеров Становского В. В., Казакявичюса С. М., Ремневой Т. А., Кузнецова В. М. (патент RU 2 416 748 C1), а также верифицированный, предложенный Н. Р. Щербаковым метод расчета динамического состояния систем передачи движения на основе эксцентриково-циклоидального зацепления позволяют инженерам-конструкторам создавать новые технически надежные механизмы.

Литература:

1. Патент № 2385435 C1 Российская Федерация, МПК F16H 55/08, F16H 1/08, F16H 19/04. Эксцентриково-циклоидальное зацепление составных зубчатых профилей: № 2008150967/11: заявл. 22.12.2008: опубл. 27.03.2010 / В. В. Становской, С. М. Казакявичюс, Т. А. Ремнева [и др.]. — EDN WFLJNW.
2. Леонтьев, М. Ю. Обзор достоинств и недостатков эксцентриково-циклоидального зацепления / М. Ю. Леонтьев, В. А. Раевский, А. Е. Смоловик // Актуальные проблемы гуманитарных и естественных наук. — 2016. — № 7–5. — С. 54–57. — EDN WFVRPJ.
3. Щербаков Н. Р. Математическое и компьютерное моделирование динамического состояния систем передачи движения: Диссертация доктора физико-математических наук. — Томск, 2009. — 213 с.
4. Филипенков А. Л. Сравнение несущей способности эксцентриково-циклоидального и эвольвентного зацепления. — Текст : электронный. — URL: https://ec-gearing.ru/img/17082016.pdf (дата обращения: 04.07.2025).