Ключевые слова: маршрутизация, комбинаторная оптимизация, сети больших масштабов.

Введение

В современном мире почти безграничной информации, социального роста, развития городов, маршрутов, сетей типа Интернет, всё больше встаёт вопрос об оптимизации их работы. К этой сфере относится проблема коммивояжёра (Travel Salesman Problem –– задача поиска наиболее оптимального (с наименьшими затратами) маршрута, проходящего через все вершины планарного графа, притом только один раз. В предлагаемой статье реализуется алгоритм поиска оптимального набора маршрутов для сетей больших масштабов методом муравьиной колонии. В последнее время методы, основанные на природных закономерностях, — Natural Computing — отлично показывают свою эффективность. Взять, к примеру, всем известные нейронные сети. Данный метод тоже использует глобальные природные принципы, реализующиеся в нашем мире.

Основная часть

Алгоритмы муравьиной колонии впервые были предложены в середине 90-х Dorigo, Maniczzo и Colorni как метод решения трудных комбинаторных оптимизационных задач, таких как задача коммивояжера и квадратичная задача о назначениях. С тех пор алгоритмы муравьиной колонии активно развивались и стали применяться к другим задачам дискретной оптимизации [1].

Имитация самоорганизации муравьиной колонии составляет основу муравьиных алгоритмов оптимизации — нового перспективного метода природных вычислении. Колония муравьев может рассматриваться как многоагентная (под агентами мы можем рассматривать как сигналы в сети, так и движущиеся транспортные средства) система, в которой каждый агент (муравей) функционирует автономно по очень простым правилам. В противовес почти примитивному поведению агентов, поведение всей системы получается на удивление разумным.

Поведение муравьев при транспортировании пищи, преодолении препятствии, строительстве муравейника и других действиях зачастую приближается к теоретически оптимальному. Муравьи обмениваются между собой информацией, притом не только прямыми способами, но и косвенными — с помощью феромонов (так называемый тип взаимодействия стигмержи). Именно это отличительная черта социальности, присущей насекомым, позволяет находить наиболее эффективные решения.

Рис. 1. Сеть гнезд суперколонии муравьев Formica lugubris [4]

Сеть муравейников близка к минимальному основному дереву, соединяющему все гнезда колонии — вершины графа.

Для построения наиболее оптимального маршрута муравьи следуют определённому алгоритму, который продемонстрируем на тривиальном примере.

1. Первый муравей находит источник пищи (F) любым способом (а), а затем возвращается к гнезду (N), оставив за собой тропу из феромонов (b).
2. Затем муравьи выбирают один из четырёх возможных путей, затем укрепляют его и делают привлекательным.
3. Муравьи выбирают кратчайший маршрут, так как феромоны с более длинных путей быстрее испаряются.

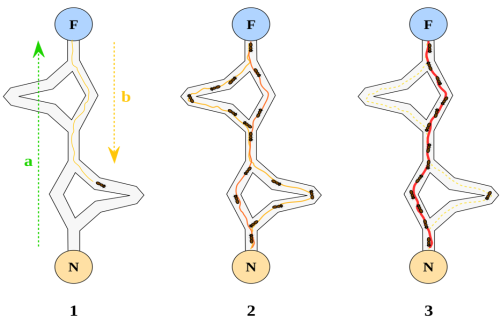
Рис. 2

Среди экспериментов по выбору между двумя путями неравной длины, ведущих от колонии к источнику питания, муравьи, как правило, используют кратчайший маршрут. [3]

Модель такого поведения заключается концептуально в следующем.

— Первый муравей (так называемый «Блиц») проходит случайным образом от колонии.

— Если он находит источник пищи, то возвращается в гнездо, оставляя за собой след из феромона.

— Феромоны привлекают других муравьёв находящихся вблизи, которые вероятнее всего пойдут по этому маршруту.

— Вернувшись в начало они укрепят феромонную тропу.

— Если существует два маршрута, то по более короткому, за то же время, успеют пройти больше муравьёв, чем по длинному.

— Короткий маршрут станет более привлекательным.

— Длинные пути, в конечном итоге, исчезнут из-за испарения феромонов.

Опишем формально решение оптимизационной задачи методом муравьиной колонии:

В общем, задачи комбинаторной оптимизации (Combinatorical Optimization Problems, COP) состоят из триплета: (𝑆,Ω,𝑓), где:

𝑆 — пространство решений, образованное конечным числом переменных

Ω — множество ограничений на переменные

𝑓:𝑆 ⟶ — целевая функция (функция, которую нужно минимизировать)

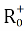
Пространство решений S определяется следующим образом: пусть дан набор дискретных переменных 𝑋 _i , 𝑖=1,…,𝑛 со значениями ∈ 𝐷 _i = { , … , }, которые заданы заранее. Набор допустимых решений 𝑆 _Ω есть набор тех решений, лежащих в S, которые удовлетворяют всем ограничениям из множества Ω.

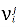
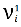
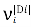
Решение 𝑠 ^∗ ∈ 𝑆 _Ω называется глобальным минимумом (или точным решением), если и только если

𝑓(𝑠 ^∗ ) ≤ 𝑓(𝑠´) ∀ 𝑠 ∈ 𝑆

Применительно к данной задаче множество всех возможных решений переобозначим как 𝐶={𝑐 _ij }, что соответствует 𝑋 _i . Далее граф 𝐺 _C (𝑉,𝐸) определим как связь компонентов множества всех решений C и множества вершин V и рёбер E. След (остаток) феромона 𝜏 _ij связан с каждым компонентом решения 𝑐 _ij . Но не стоит забывать, что он может зависеть от номера итерации, на которой сейчас находится алгоритм. То есть зависит от шага алгоритма.

Муравьи перемещаются по вершинам графа, используя информацию от феромонов, и постепенно образуют оптимальное решение. Также оставляя феромоны на вершинах и рёбрах, на которых побывали.

Эвристику метода муравьиной колонии можно описать следующими пунктами:

0. Задание графа и алгоритмических параметров.
1. Муравьиное построение решения (Construct Ant Solution)
2. Промежуточные преобразования [опционально] (DaemonActions)
3. Обновление значений феромона.

Стоит отметить, что алгоритм идёт по циклу (пункты 1–3) и завершается установленным ранее способом: либо ограничивается числом итераций, либо временем работы программы (так как алгоритм эвристический, то он не всегда находит оптимальные решения или вообще может их не находить).

Рассмотрим три итерационных шага более подробно.

1. Начальное решение представляет собой пустое множество: 𝑠 ^𝑝 = ∅. Далее на каждом последующем шаге предыдущее частное решение расширяется добавлением набором допустимых соседних вершин 𝑁(𝑠 ^𝑝 ) ⊆ 𝐶. Этот процесс можно рассматривать как построение пути на графе 𝐺 _C (𝑉, 𝐸). Разрешенные пути неявно определяются механизмом построения решений, который определяет множество соседних вершин 𝑁(𝑠 ^𝑝 ) для частного (предварительного) решения 𝑠 ^𝑝 . Как раз выбор этого множества соседних вершин и определяет дальнейшую реализацию алгоритма. Выбор соседних вершин определяется вероятностным образом на каждом конкретном шаге. Это вероятностное правило сильно отличается в различных методах алгоритма муравьиной колонии (о вариациях алгоритма речь пойдёт дальше). Наиболее известное и то, которое мы будем использовать выглядит следующим образом:

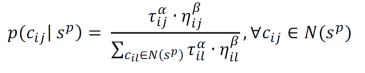
где:

𝐶 = {𝑐 _ij }, 𝑖 = 1,…, 𝑛, 𝑗 = 1,…, |𝐷 _i |

–величина влияния количества феромона на выбор решения 𝑐 _ij ;

– величина влияния эвристики для данного графа на выбор решения 𝑐 _ij . Обычно приравнивается как величина обратная длине ребра (i, j);

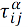
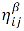
𝛼, 𝛽 – параметры, определяющие важность феромона относительно эвристической информации.

При 𝛼 = 0 выбор близлежащего города становится наиболее вероятным, то есть алгоритм превращается в жадный.

При 𝛽 = 0 выбор происходит только на основании феромонов, что приводит к субоптимальным решениям.

Компромисс между этими двумя решениями находится экспериментально и может сильно отличаться для оптимального случая в зависимости от специфики задачи. Решение не является точным и может быть даже самым неоптимальным. Но в силу удачно подобранных параметров, оно может стать наиболее эффективным.

После определения вероятности идёт так называемое DaemonActions — действия демона: после составления решения и перед преобразованиями значений феромона, часто требуют выполнения некоторые промежуточные действия. Самое частное из них — локальный поиск из имеющихся решений, то, что не может сделать муравей по отдельности.

Далее идёт обновления значений феромона на рёбрах: то есть увеличить его количество на хороших решениях и уменьшить — на плохих. То есть идёт уменьшение имеющегося на рёбрах феромона и увеличение его на тех рёбрах, где только что побывали муравьи:

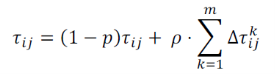
где:

𝜌 𝜖 (0,1] — параметр, называемый уровнем испарения,

— количество феромона, оставшимся после прохождения по ребру (i, j) муравьём k.

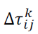
Вариации алгоритма:

1. Элитарная муравьиная система — из общего числа муравьёв выделяется специальный класс муравьёв — «элитные» муравьи. По итогам каждой итерации происходит усиление лучших маршрутов проходом по данным маршрутом этих, элитных, муравьёв. В такой системе количество элитных муравьёв является дополнительным параметром, требующим определения. Для слишком большого числа элитных муравьёв алгоритм может застрять на локальном экстремуме.
2. Max-Min Ant System (MMAS) — накладывается дополнительное условие на количество откладываемого феромона: (𝑓 _min ., _max ).
3. Пропорциональные псевдослучайные правила — использовано выше.
4. Ранговая муравьиная система — решения ранжируются по степени их пригодности для данной задачи. Чем более решение пригодно, тем больше феромонов на ней будет оставаться.
5. Длительная ортогональная колония муравьёв (COAC).

Данное описание алгоритма муравьиной колонии является первоначальной. Для адаптации под реальные программы и задачи, алгоритм, естественно, также нужно адаптировать. В данном случае алгоритм требовал адаптации под задачу маршрутизации с ограничением по грузоподъёмности.

Вывод

Основной принцип действия программы можно представить с помощью следующего псевдокода:

Initialization (вершины, матрица смежности, вместимость, запросы, количество муравьёв, параметры 𝜌, 𝛼, 𝛽 )

For каждого муравья:

While все вершины не будут посещены:

Do выбирать каждую следующую вершину (v1, … , vk) с вероятностью p(i, j)

If (вместимость > суммарный запрос вершин пути, добавить путь (v1, …, vk) к solution.

Добавить все solution и длину каждой length в массив solutions.

For каждого ребра

Do изменить количество феромонов t _ij

If (длина минимального пути Solutions < BestSolution), то

BestSolution = минимальный путь из Solutions.

Программа была реализована на языке Python с использованием библиотек numpy, getopt, reduce, random, RedExService.

Для адаптации алгоритма были применены следующие идеи и модификации: добавлен начальный пробег муравья, пока не будут обойдены все вершины, несмотря на вместимость; модифицирована формула изменения феромона, которая теперь учитывает не каждого муравья по отдельности, а муравья как множество агентов (множество машин применительно к задачи логистики); изменен способ нахождения решения, которые основывается на сравнении множества последовательностей путей для каждого муравья. Сам же муравей представляет собой группу агентов.

Литература:

1. Ran Raz, Avishay Tal «Oracle separation between BQP and PH», 2012.
2. Ivan Brezina Jr. Zuzana Čičková, 2011, «Solving the Travelling Salesman Problem Using the Ant Colony Optimization».
3. Hoang Xuan Huan, Nguyen Linh-Trung, Do Duc Dong, Huu-Tue Huynh, 2012, «Solving the Traveling Salesman Problem with Ant Colony Optimization: A Revisit and New Efficient Algorithms», DOI: 10.21553
4. J.-L. Deneubourg, S. Aron, S. Goss et J.-M. Pasteels, The self-organizing exploratory pattern of the Argentine ant, Journal of Insect Behavior, volume 3, page 159, 199 34.