В статье рассматривается задача моделирования динамической системы — простого маятника. Представлен подход к численному решению системы с помощью SciPy и визуализации поведения с помощью Matplotlib. Также реализована система управления с применением PID-регулятора. Результаты демонстрируют возможность стабилизации маятника и расширяемость метода на более сложные задачи.
Ключевые слова: маятник, PID-регулятор, моделирование, Python, динамическая система, SciPy, Matplotlib.
Введение
Моделирование динамических систем играет ключевую роль в технических науках и инженерных приложениях. Оно позволяет анализировать поведение объектов, находящихся под действием различных сил, разрабатывать системы управления и оптимизировать параметры процессов. Язык программирования Python, благодаря богатому набору библиотек для научных вычислений, предоставляет эффективные инструменты для численного моделирования и визуализации сложных физических явлений. [2] В данной работе рассматриваются примеры моделирования простого математического маятника, а также реализации системы автоматического управления с помощью PID-регулятора. Используются библиотеки SciPy и Matplotlib, что делает решение доступным для практического применения и адаптации под конкретные задачи. [1]
Математическая модель простого маятника
Маятник представляет собой простую механическую систему с одной степенью свободы. Его движение определяется действием силы тяжести, вызывающей колебания при отклонении от положения равновесия. Для описания динамики такой системы используется система дифференциальных уравнений, отражающая зависимость угла отклонения и угловой скорости от времени. [4] Для численного моделирования уравнения движения преобразуются к форме, удобной для расчёта с использованием стандартных численных методов. В данной работе используется метод Рунге–Кутты, реализованный в библиотеке SciPy. При рассмотрении управляемой системы в модель вводится внешнее воздействие, имитирующее управляющий момент. Это позволяет применять алгоритмы автоматического управления, в частности PID-регулятор, который обеспечивает возврат маятника в вертикальное положение при отклонениях. [3]
Численное моделирование
Моделирование движения маятника выполнено в среде Python с использованием библиотеки SciPy. Для численного решения системы дифференциальных уравнений применялся метод Рунге–Кутты 4–5 порядка, реализованный в функции solve_ivp. В качестве начальных условий задан угол отклонения, равный 45 градусам, при нулевой угловой скорости. Временной интервал моделирования составил 10 секунд с равномерной дискретизацией на 300 точек. Параметры маятника включают длину в один метр и ускорение свободного падения, равное 9,81 м/с². [5]
В результате работы алгоритма получены массивы значений угла и угловой скорости во времени, которые легли в основу визуализации и анализа динамического поведения системы.
Управление маятником с помощью PID-регулятора
Для стабилизации маятника в вертикальном положении применён PID-регулятор — один из самых распространённых алгоритмов управления в инженерной практике. Он учитывает текущее отклонение, скорость его изменения и накопленную за время ошибку, что позволяет системе плавно и точно возвращаться в заданное состояние. Управляющее воздействие рассчитывается на каждом шаге моделирования и добавляется в уравнение движения. Реализация регулятора выполнена в виде отдельного программного блока. Коэффициенты PID-регулятора настраиваются вручную, подбираются таким образом, чтобы обеспечить устойчивое поведение: маятник возвращается в вертикальное положение и затухает без колебаний.
Визуализация результатов
Для наглядной оценки поведения системы были построены графики изменения угла и угловой скорости маятника во времени. Визуализация выполнена с использованием библиотеки matplotlib.
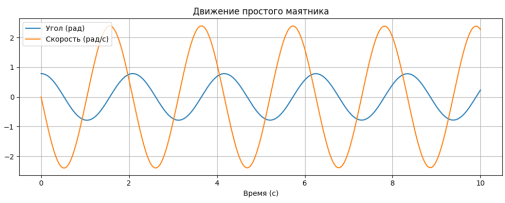
Рис. 1. Свободное движение маятника без управления
На первом рисунке показано свободное движение маятника без какого-либо управления. Видно, что колебания происходят периодически, без затухания. Это соответствует теоретической модели без сопротивления и внешнего воздействия.
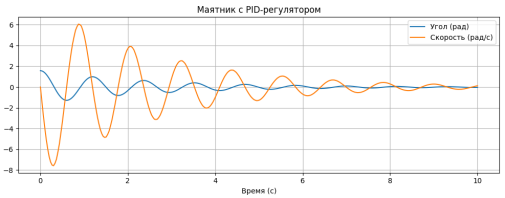
Рис. 2. Поведение маятника с подключённым PID-регулятором
На втором рисунке представлено поведение маятника с подключённым PID-регулятором. В начальный момент времени маятник отклонён от вертикали, но за счёт управляющего сигнала система стабилизируется. Угол отклонения и скорость постепенно стремятся к нулю. Это демонстрирует эффективность предложенного способа управления.
Выводы
В ходе работы была реализована численная модель движения простого маятника, дополненная системой управления на основе PID-регулятора. Применение языка Python и библиотек SciPy и Matplotlib обеспечило как решение уравнений, так и визуальный анализ поведения системы.
Моделирование показало, что при отсутствии управления маятник совершает колебания вокруг положения равновесия, тогда как с подключением регулятора система стабилизируется. Это подтверждает эффективность алгоритма PID для задач удержания и коррекции положения.
Реализованное решение универсально и может служить основой для более сложных моделей — в том числе с учётом трения, внешних воздействий или для многозвенных систем. Работа демонстрирует практическую применимость численного моделирования и алгоритмов управления в технических науках и инженерных разработках.
Литература:
1. Сысоева М. В., Сысоев И. В. Программирование для «нормальных» с нуля на языке Python: Учебник. — М.: Базальт СПО; МАКС Пресс, 2018.s
2. Алферова Тамара Викторовна, Трохова Татьяна Анатольевна Компьютерное моделирование элементов динамических систем в python // Агротехника и энергообеспечение. 2021. № 3 (32).
3. Морозов А. Ю., Ревизников Д. Л. Моделирование динамических систем с интервальными параметрами. Обзор методов и программных средств.
4. Чибисов А. В., Попов А. Г., Мозговой Н. А., Пиджаков В. А. Автоматическая настройка ПИД-регулятора с применением машинного обучения для обеспечения стабильной работы автономных электронных систем при термоциклировании.
5. Чхартишвили Г. С. Автоматизированное моделирование линейных динамических систем: методическое пособие. — М.: Изд-во МЭИ, 2004.

