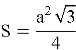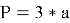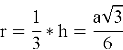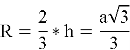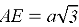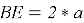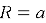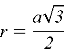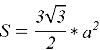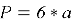В статье автор исследует основные формулы для правильных многоугольников и приводит примеры решения задания 1 из ЕГЭ по математике (профиль).

Ключевые слова: единый государственный экзамен (ЕГЭ), математика (профиль), правильный многоугольник.

Значительная часть школьников России выбирают для сдачи единого государственного экзамена (ЕГЭ) профильную математику. Они уделяют большую часть времени подготовке. Первая часть в заданиях ЕГЭ по математике решается гораздо легче, чем вторая. Однако, даже там есть «подводные камни» и могут возникнуть различные сложности при выполнении заданий. Следовательно, обучающимся нужно знать различные пути и способы решения задач.

При решении задания 1 ученики умело оперируют общеизвестными и базовыми формулами, однако, далеко не каждый помнит формулы и особенности решения задач с правильными многоугольниками. Зная необходимые формулы, можно решить задачу в одно действие, тем самым значительно облегчив решение варианта и сэкономив время на выполнение заданий.

«Правильный многоугольник — это выпуклый многоугольник, у которого равны все стороны и все углы» [1, С. 270].

Наиболее часто употребляемыми фигурами в первом задании являются равносторонний треугольник и шестиугольник. Рассмотрим основные особенности данных фигур:

1. Равносторонний треугольник. В данном треугольнике равны все углы и стороны, а градусная мера каждого угла составляет 60˚. Равносторонний треугольник представлен на рисунке 1.

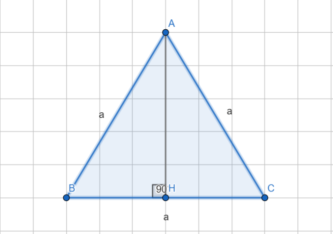
Рис. 1. Равносторонний треугольник ABC

Стоит отметить, что при проведении высоты в данном треугольнике образуются два равных прямоугольных треугольника, поэтому сторона , тогда высота равностороннего треугольника находится по формуле:

.

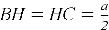
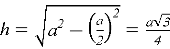
Помимо нахождения высоты, в задачах могут быть использованы также следующие формулы, представленные в таблице 1.

Таблица 1

Основные формулы равностороннего треугольника

2. Равносторонний шестиугольник. В данном многоугольнике равны все стороны и углы, при этом градусная мера каждого угла составляет 120˚. Правильный шестиугольник представлен на рисунке 2.

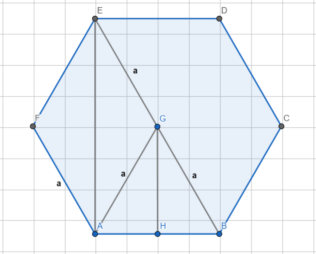
Рис. 2. Правильный (равносторонний) шестиугольник

Заметим, что данный шестиугольник состоит из шести правильных (равносторонних) треугольников, одна из вершин которых лежит в центре вписанной и описанной окружности. Поэтому основные формулы для правильного шестиугольника имеют следующий вид (таблица 2).

Таблица 2

Основные формулы правильного шестиугольника

Рассмотрим примеры решения задания 1 с использованием этих формул.

1. Сторона равностороннего треугольника равна . Найдите радиус окружности, вписанной в этот треугольник (см. рисунок 3) [2].

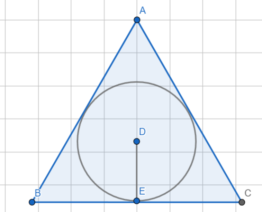
Рис. 3. Чертёж к первой задаче

Решение. Радиус вписанной окружности в равносторонний треугольник вычисляется по формуле: (а — сторона правильного треугольника). Следовательно, радиус будет равен

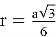
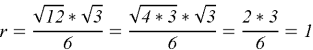
Ответ: 1.

2. Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности (см. рисунок 4) [2].

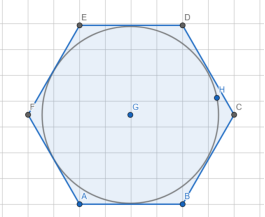
Рис. 4. Чертёж ко второй и третьей задаче

Решение. Так как периметр — это сумма длин всех сторон, то сторона правильного шестиугольника будет равна .

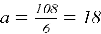
Радиус окружности, описанной вокруг правильного многоугольника, равен его стороне, следовательно, диаметр окружности равен

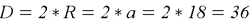
Ответ: 36.

3. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен (см. рисунок 4) [2].

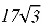
Решение. Данную задачу можно решить двумя способами: с использованием формул для правильных многоугольников или аналитическим методом с построением чертежа.

Рассмотрим первый способ. Радиус вписанной окружности в правильный шестиугольник вычисляется по формуле: . Тогда сторона шестиугольника равна .

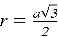
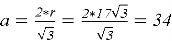
Рассмотрим второй способ. Проведём между вершинами диагонали и получим шесть равносторонних треугольников, как представлено на рисунке 5.

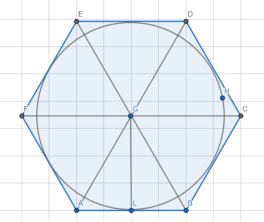
Рис. 5. Чертёж решения третьей задачи

Рассмотрим треугольник AGB, проведём высоту GL (она также является медианой, биссектрисой и радиусом списанной окружности). Треугольник GLB — прямоугольный. Пусть так как это катет, лежащий напротив угла 30˚, то .

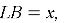
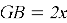
Воспользуемся теоремой Пифагора:

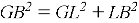
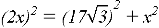
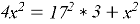
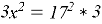
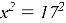
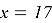
Тогда сторона шестиугольника равна .

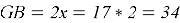
Ответ: 34.

Таким образом, с помощью формул для правильных многоугольников можно решать задачи более удобным и лёгким способом, избегая громоздкого и запутанного решения. Обучающимся будет полезно знать и помнить данные формулы, чтобы иметь возможность применить их на экзамене.

Литература:

1. Атанасян Л. С., Бутузов В. Ф. и др. Геометрия 7–9 классы. — М.: Просвещение, 2022. — 383 с.
2. [Электронный ресурс] URL: https://math-ege.sdamgia.ru/?ysclid=maqzo3nvga701229417