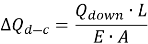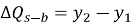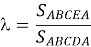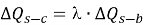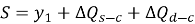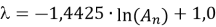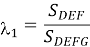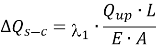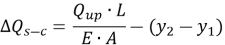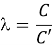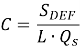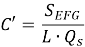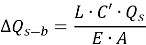Из-за многочисленных преимуществ по сравнению с статическим испытанием на нагрузку сверху вниз двунаправленное испытание на нагрузку с использованием ячейки Остерберга (O-cell) становится все более популярным способом определения предельной несущей способности свайного фундамента. В данной статье представлен систематический обзор существующих методов (оригинальный метод, модифицированные методы) для построение эквивалентной кривой с использованием результатов испытаний O-cell для буровых свай. Обоснованность методов построения эквивалентной кривой критически оценивается с помощью параметрического исследования и полевых исследований, в которых бок о бок проводились статические испытания и двунаправленные (O-cell) испытания нагрузки.

Ключевые слова: испытания сваи, полевые испытания свай, методы построения эквивалентно кривой при испытаниях сваи методом Остерберга (O-cell).

Введение

Испытание по методу Остерберга (ячейка Остерберга O-cell), которое получило свое название в честь имени своего создателя Джорджа О. Остерберга, широко используется для прогнозирования поведения буровых свай большого диаметра под нагрузкой. Впервые данный метод был применен на практике в 1984 и получил большую популярность, за счет своей доступности, экономичности и высокой производительности [1]. Ячейка O-cell работает в двух направлениях вверх против трения по боковой поверхности грунта и вниз против сопротивления под острием сваи, тем самым разделяя верхний и нижний компоненты сопротивления. Из-за различий в направлении и месте приложения нагрузки при двунаправленном испытании кривые на графике «нагрузка-перемещение» должны быть преобразованы в эквивалентную кривую, аналогичную результатам статического испытания «сверху вниз».

В 1996 году Огура показал с помощью полномасштабных испытаний, в которых сваи сначала поднимались с помощью О-cell, а затем опускались, что конечное боковое трение вверх и вниз было одинаковым [2]. При любой произвольной нагрузке вниз на графике «нагрузка-перемещения» наблюдается осадка. Затем определяется нагрузка для этого перемещения на графике «снизу вверх». Сумма нагрузок вверх и вниз при этом перемещении является эквивалентной нагрузкой сверху вниз для этого испытания.

Оригинальный метод (метод Остерберга 1998)

В 1998 году Остерберг описал метод построения эквивалентной кривой сверху вниз из данных испытания [3]. Эта кривая изначально строится, предполагая, что свая жесткая (несжимаемая) и что трение по боковой поверхности вверх равно трению по боковой поверхности вниз. Но данный метод имеет свои допущения: 1) не учитывается сжатие сваи от нагрузки на острие; 2) перемещение верхнего компонента части сваи в месте приложения нагрузки на измерения сопротивления по боковой поверхности уже включает в себя частичное смятие сваи при испытании снизу вверх; 3) смятие сваи верхнего компонента может не совпадать со смятием сваи нижнего компонента при приложении одной и той же нагрузки, из-за различий в механизме передачи нагрузки на сваю и грунт; 4) прямое суммирование кривых «нагрузка-перемещение» вверх и вниз, полученных при испытании Остерберга при аналогичных смещениях ограничивается минимальным перемещением, наблюдаемым в двух направлениях. Таким образом, кривая, имеющая меньшее смещение, должна быть экстраполирована, чтобы извлечь пользу из всех показаний. Обычно для этого производится корректировка при помощи гиперболической кривой [5].

Модифицированные методы (Квон, Ким и Миссион, Ким и Чанг и Мессад)

Но затем такие ученые, как Квон [6], Ким и Миссион [7], Ким и Чанг [8] и Мессад [9] предложили эмпирические модифицированные методы построения эквивалентной кривой. Все эти методы имеют одну и ту же суть решения проблемы. Все они рассматривают сжатие сваи, как при испытаниях на статическую нагрузку, вызванное трением по боковой поверхности (Q _s-c ) и сопротивлением под острием(Q _d-c ), так и при испытании сваи методом O-cell, вызванное только трением по боковой поверхности (Q _s-b ). Было одно допущение, что сжатие, вызванное нагрузкой при статическом испытании, отличается от сжатия, вызванного при испытании O-cell, и соотношение между этими двумя значением () зависит от трения по боковой поверхности единичной сваи. Трение по боковой поверхности единичной сваи — это один из идеальных случаев, при котором поверхностное трение увеличивается линейно с глубиной (см.рис.1а). Соответствующие кривые передачи нагрузки, полученные во время статических испытаний (сверху-вниз) и испытания O-cell (двунаправленная нагрузка) показаны на рис. 1b и 1e. Смысл поправочного коэффициента для сжатия сваи в месте приложения осевой нагрузки заключается путем определения отношения площади распределения нагрузки между статическим испытанием сваи сверху-вниз и испытанием O-cell снизу-вверх [4].

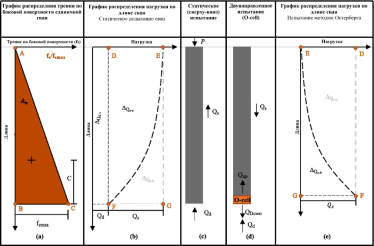
Рис. 1. График идеального случая прочности на сдвиг и соответствующие кривые передачи нагрузки

(а) Распределение трения на единицу поверхности и нормализованный профиль прочности на сдвиг. (b) Кривая передачи нагрузки во время статического испытания. (c) Схематический рисунок статического испытания. (d) Схематический рисунок испытания O-cell. (e) Кривая передачи нагрузки во время испытания O-cell.

На графике передачи нагрузки по длине видно, что сжатие, вызванное статической нагрузкой больше, как представлено областью DEF на рис. 1b. Таким образом, чтобы скорректировать смещение, измеренное в O-cell испытании, необходимо оценить и добавить дополнительные сжатия, вызванные трением по боковой поверхности и сопротивлением на острие в испытании на статическую нагрузку. Все исследователи согласились использовать уравнение (1) для оценки дополнительного сжатия, вызванного нагрузкой на острие сваи в испытании статической нагрузкой сверху-вниз, так как испытание на статическую нагрузку проводится не всегда.

где:

— сжатие сваи на нагрузку на острие сваи при статическом испытании сверху-вниз, м.

— приложенная нагрузка на острие сваи при испытании O-cell, кН.

— длина сваи, м.

— модуль упругости сваи, МПа.

— площадь поперечного сечения сваи, м.

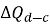
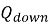
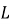
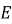
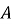
В 2005 году Квон и др предложили модификацию исходного метода построения эквивалентной кривой. Они сначала оценили сжатие сваи, произведенное испытанием Остерберга (Q _s-b ) путем прямого сравнения измеренных смещений верха сваи (у1) и ячейки (у2) при различных приложенных нагрузках, как представлено в уравнении

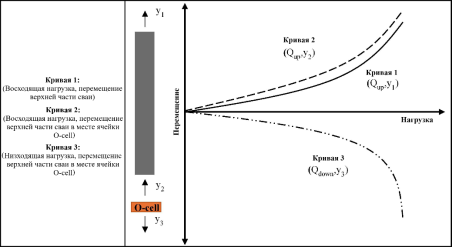
Рис. 2. Схематический график кривых, полученных по результатам испытаний О-cell

Затем они оценили λ (отношение сжатия из-за нагрузки при статическом испытании к сжатию в двунаправленном испытании), изучив кривую передачи нагрузки двунаправленного испытания, полученную из измерений тензодатчиков.

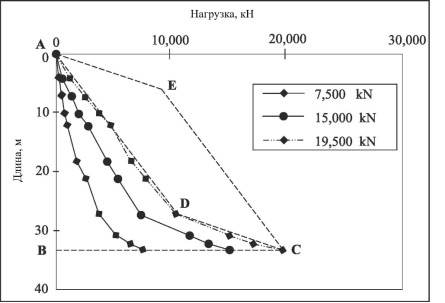
Рис.3. Кривые передачи нагрузки снизу-вверх во время испытания O-cell

На рис. 3. показана кривая распределения нагрузки, измеренная на месте во время теста O-cell. Сначала они построили линии AE и EC, параллельные линиям CD и AD соответственно. Затем они нашли λ, оценив отношение между площадями ABCEA и ABCDA, как показано в уравнении (3). Предполагается, что линии AE и EC обеспечивают виртуальное представление перевернутой кривой распределения нагрузки, которая была бы получена в результате испытания на статическую нагрузку, когда нагрузка, приложенная сверху, равна максимальному боковому сдвигу.

Затем они нашли Q _s-c (сжатие сваи от нагрузки за счет трения по боковой поверхности при статическом испытании).

В 2011 году Ким и Миссион провели параметрическое исследование на реально полученных данных. Они разработали общее логарифмическое уравнение для определения , которое зависит от идеализированной площади распределения прочности на сдвиг An.

В 2012 году Ким и Чангу предложили 2 метода оценки эквивалентной кривой, они зависели известно распределение нагрузки или нет. Когда распределение нагрузки известно, Ким и Чангу оценили соотношение , согласно рис.1е по уравнению (7) и затем нашли значение Q _s-c по уравнению (8).

Где:

— направленная вверх нагрузка, приложенная на уровне ячейки O-cell при заданном смещении.

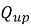
Если распределение нагрузки было неизвестно, Ким и Чунг использовали уравнение (9) для оценки Q _s-c . После оценки Q _s-c , они оценили Q _d-c по уравнению (1). Затем они добавили оба значения к перемещению верхней части сваи (у1) для нахождения (S), как показано в уравнении (5).

В 2015 году Массада определили , как соотношение С/С’, где С и C’ определяется как коэффициент Леонардса и Ловелла, который определяется по формуле (11).

После оценки λ, он предложил использовать уравнение (2) или (12) для оценки Q _s-b , в зависимости от доступной информации. Затем он использовал уравнение (4) для расчета Q _s-c . Наконец, он оценил (S) с помощью уравнения (5). Практика показала, что метод Массада дает более сходимые результаты с численными расчетами.

Вывод

Это исследование было направлено на оценку доступных эмпирических методов для интерпретации результатов испытания нагрузки в двух направлениях (O-cell) для построения кривой зависимости эквивалентной статическим испытаниям. Методы, рассмотренные в этом исследовании, были оригинальный метод, методы Квон, Ким и Миссион, Ким и Чанг и Мессад. Первоначальный метод построения эквивалентной кривой нагрузки сверху вниз, предложенный Остербергом, предполагает, что свая жесткая, и не учитывает в полной мере общее упругое укорочение из-за осевых компонентов нагрузки от трения по боковой поверхности и сопротивления под острием. Модифицированные методы учли данные допущения и стали принимать сжатие сваи для построения эквивалентной кривой, но сжатие сваи при статических испытаниях и испытаниях ячейкой O-cell отличается на показатель , найти который можно по одному из вышеперечисленных эмпирических методов.

Литература:

1. Tony Ruban. Pile load testing of concrete belled pile and rock socket pile using the Osterberg load cell. 2011 г.
2. Ogura et. al. Appliction of Pile TOE Tests to Cast-in-Place and Precast Piles. 1996 г.
3. Osterberg J. O. The Osterberg Load Test method for Drilled Shafts and Driven Piles — the first ten years. 1998 г.
4. Kwon OS, Choi Y, Kwon O, Kim MM. Comparison of the bidirectional load test with the top–down load test. 2005 г.
5. H. Seo, R. B. Moghaddam, W. D. Lawson. Assessment of methods for construction of an equivalent top loading curve from O-cell test data. 2016 г.
6. O. S. Kwon, Y. Choi, O. Kwon, M. M. Kim. Comparison of the bidirectional load test with the top-down load test. 2005 г.
7. H. J. Kim, J. L. Mission. Improved evaluation of equivalent top-down load-displacement curve from a bottom-up pile load test. 2011 г.
8. S. R. Kim, S. G. Chung. Equivalent head-down load vs. Movement relationships evaluated from bi-directional pile load tests. 2012 г.
9. F. Massad. On the interpretation of the bidirectional static load test. 2015 г.
10. Hoyoung Seon, Rozbeh B. Moghaddam, William D. Lawson. Assessment of methods for construction of an equivalent top loading curve from O-cell test data. 2016 г.
11. Jose Leo C. Mission, Hyeong-Joo Kim. Design charts for elastic pile shortening in the equivalent top–down load–settlement curve from a bidirectional load test. 2010 год.