1. Introduction

We consider numerical solving the hyperbolic equation

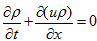
equipped with suitable initial condition for known velocity coefficient

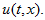
Among the successful numerical methods for solving this equation we mention such nonoscillatory conservative finite difference shemes as TVD (total variation diminishing), TVB (total variation bounded), and ENO (essentially nonoscillatory) ones (see, for example, [1]- [14] and the reference there).

In order to highlight the essential ingredients of suggested approach we begin with one-dimensional problem, keeping in mind that we shall extend these methods in subsequent papers. Moreover, for simplification we take periodic data to avoid a description complication for inessential issues connected with boundary-value conditions.

2. The statement of problem and the main theorem

Thus, in the rectangle 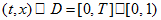consider equation

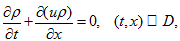(1)

with initial condition

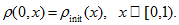(2)

Coefficient 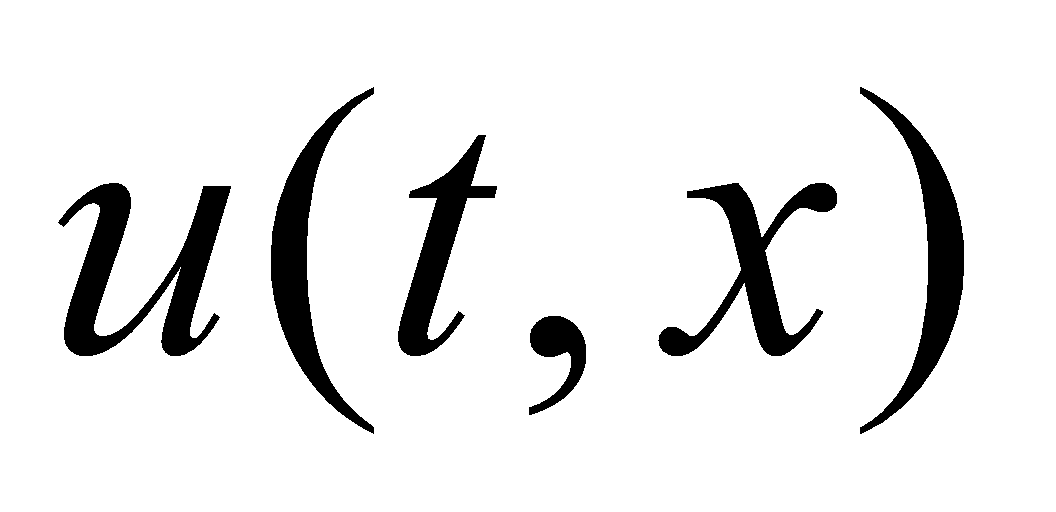is given at 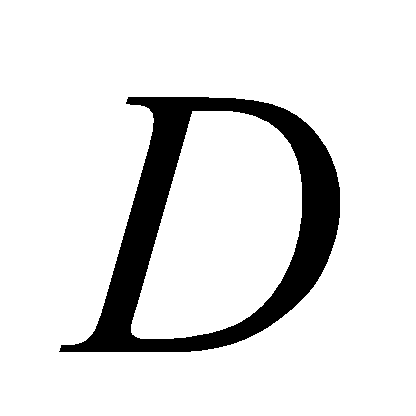and functions are supposed periodical in 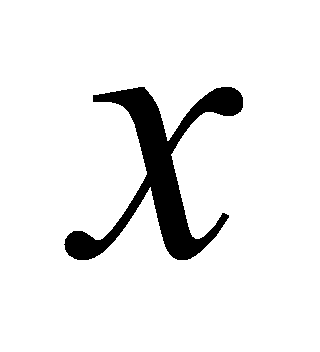with period 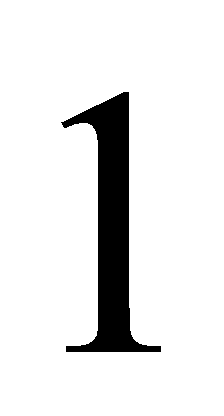and are smooth enough for further considerations.

One of difficulties in solving (1)-(2) is that solution may contain discontinuities even for smooth data. But we start our considerations for the case of smooth solution.

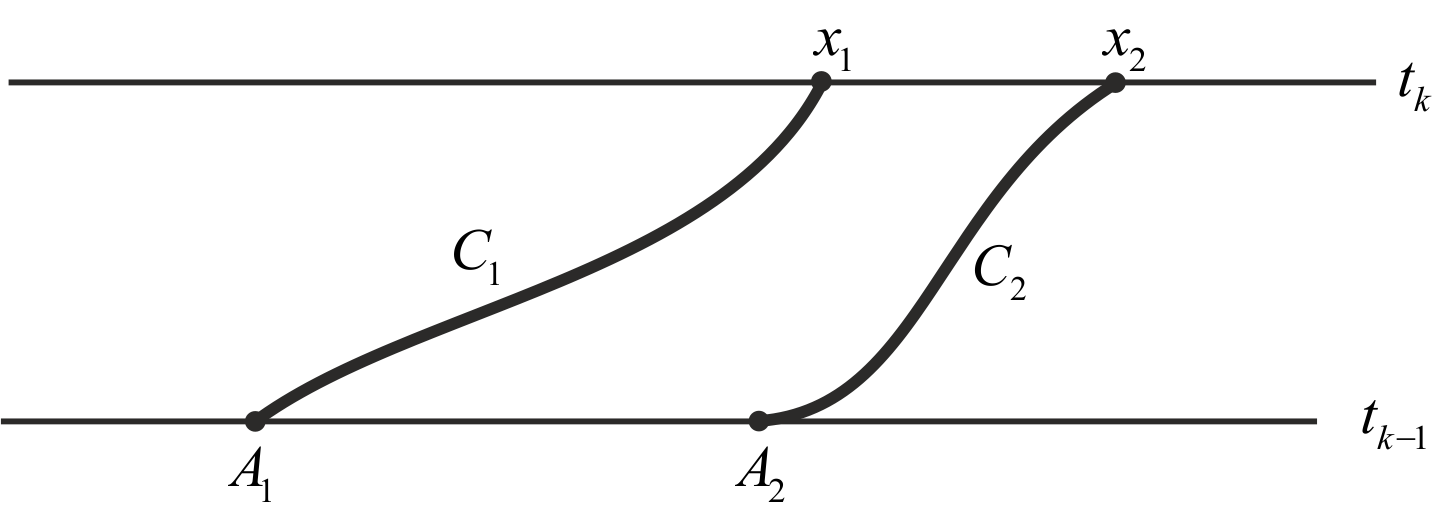
Let us take two time lines 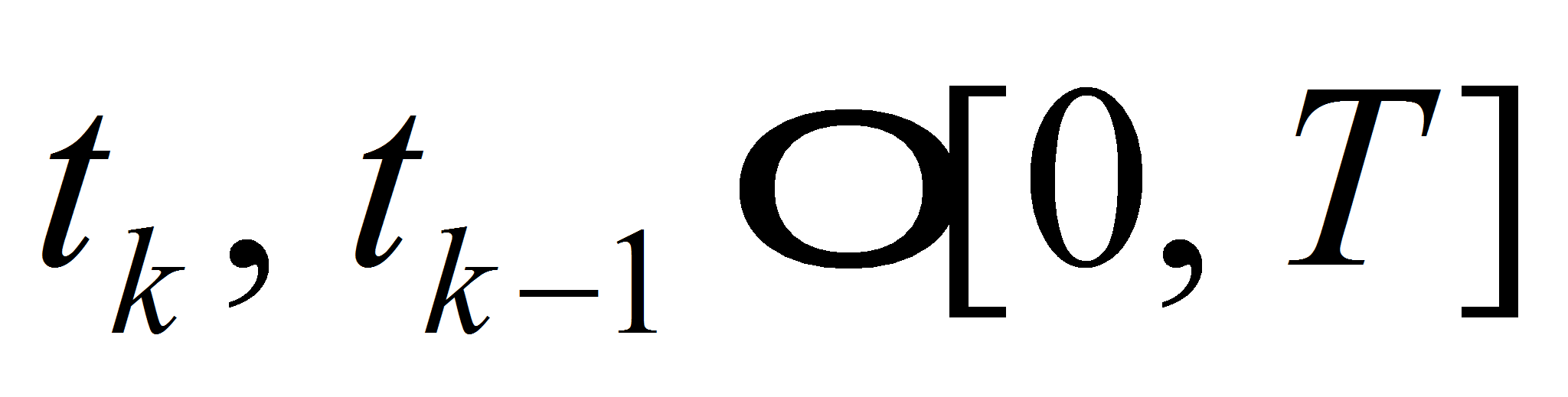with 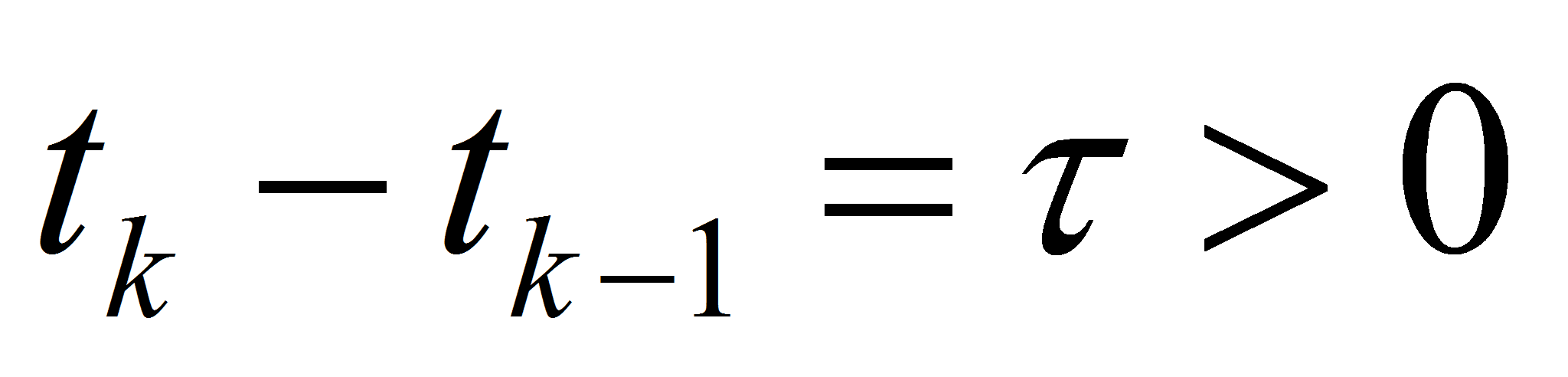and two nodes

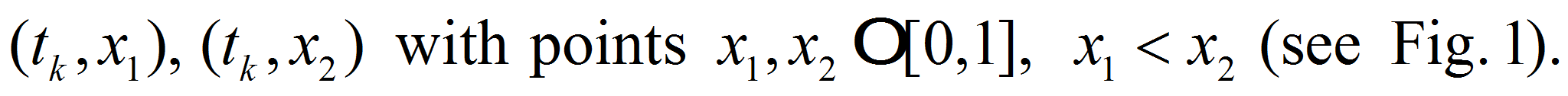
For both these nodes we construct the characteristics 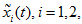of equation (1) at segment 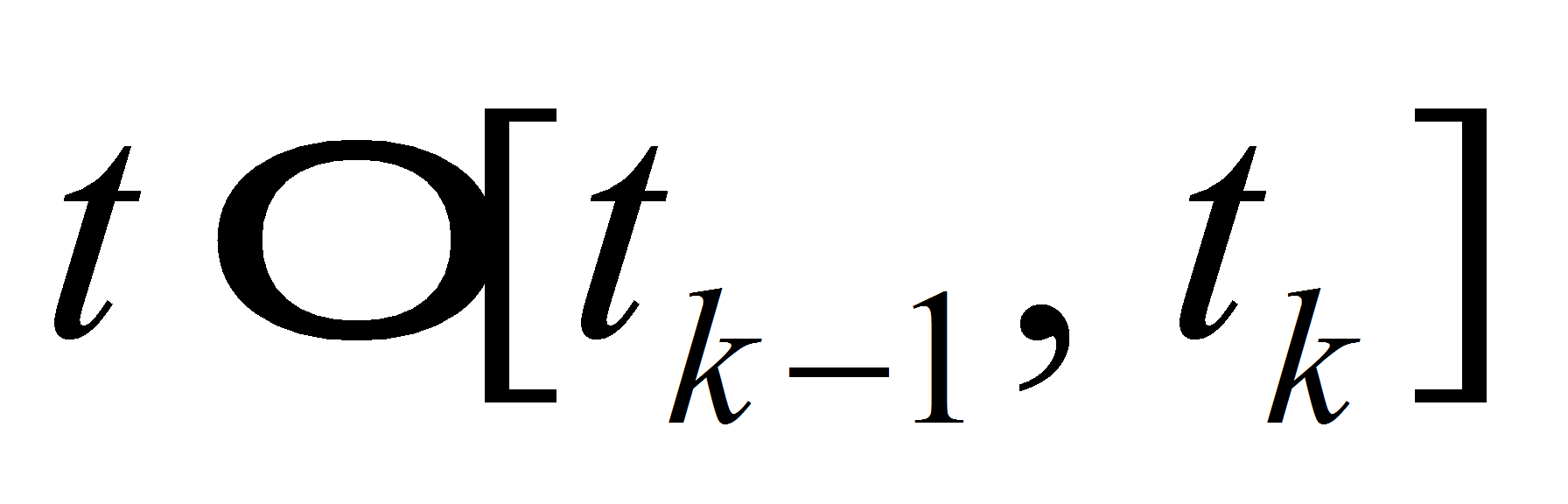[16, 17]. They satisfy the ordinary differential equation with different initial values:

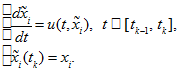(3)

Fig. 1. Trajectories

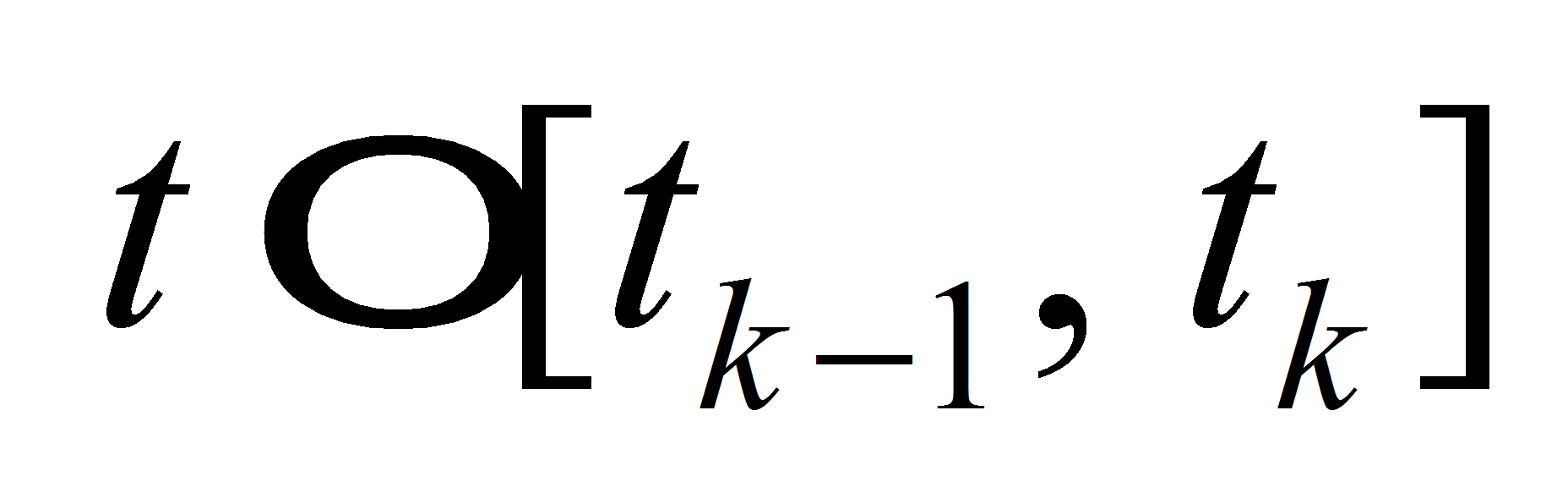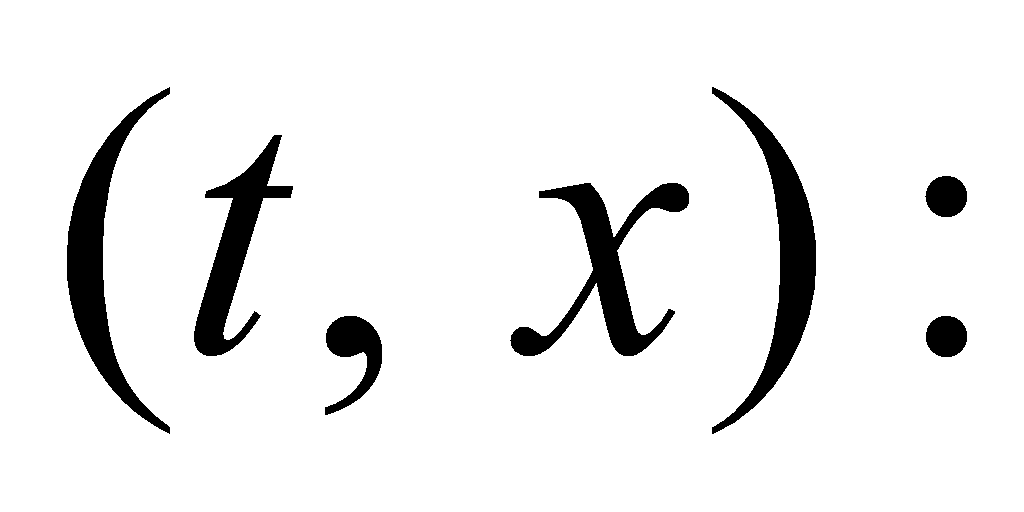
These characteristics define two trajectories for in plane 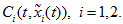Each of these trajectories crosses line 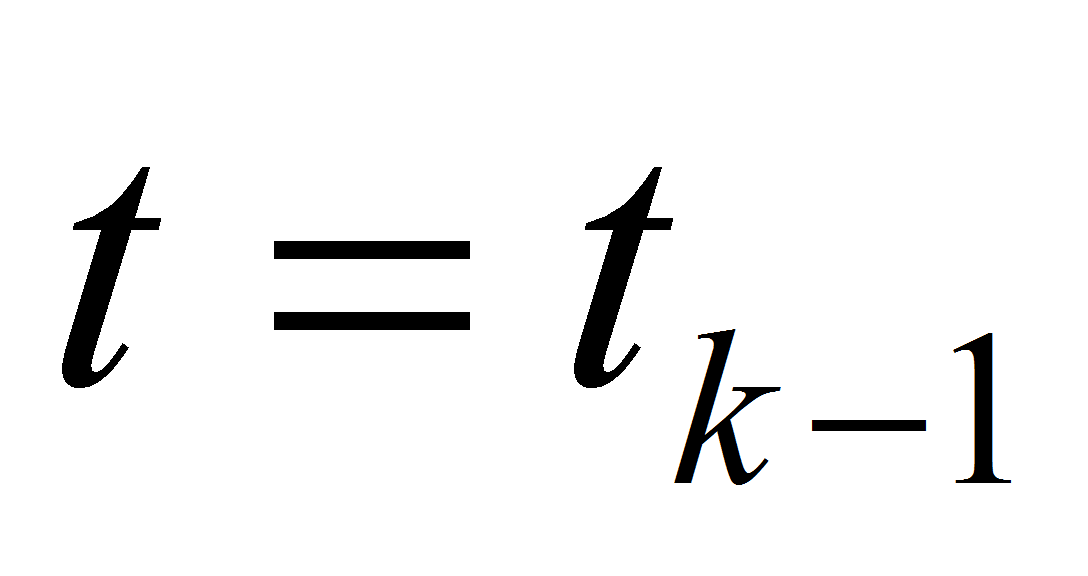in some point 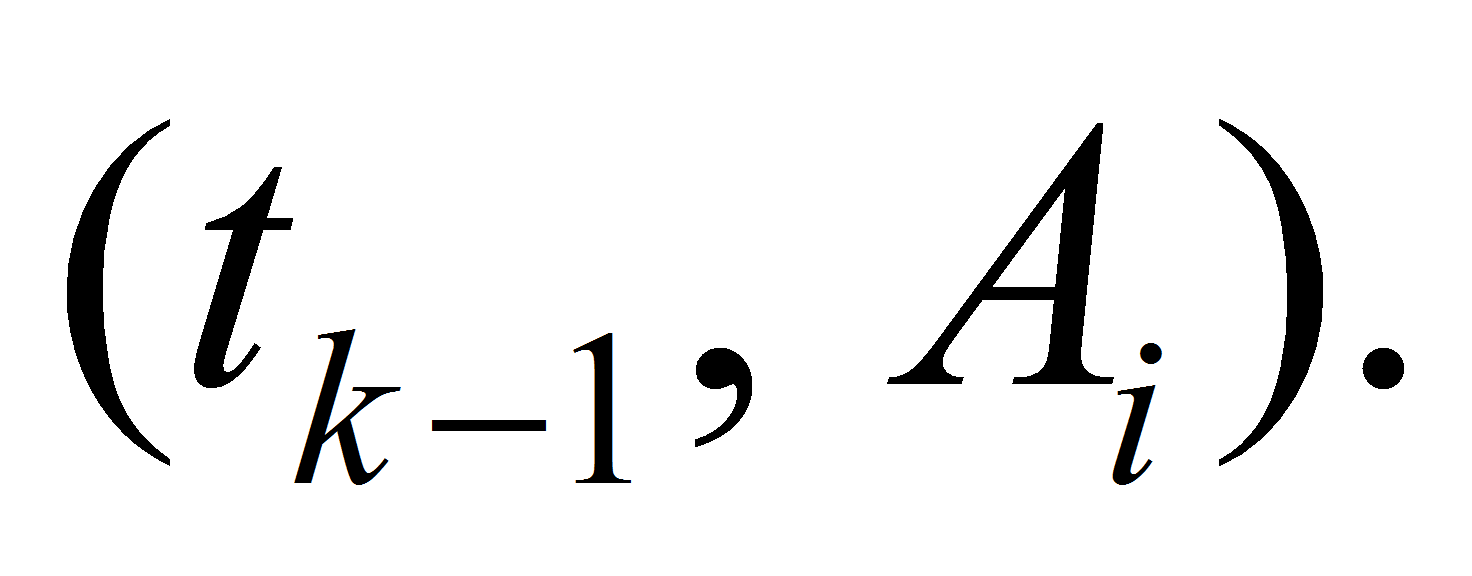We suppose that they are not mutually crossed and therefore

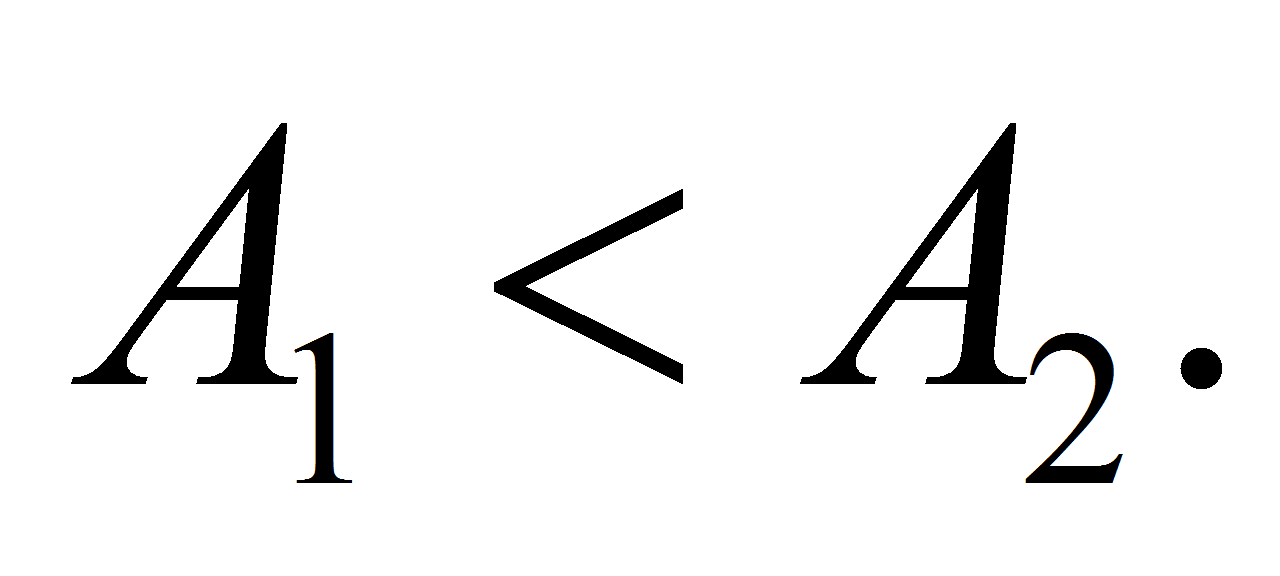
Theorem 1. For smooth solution of equation (1) we have equality

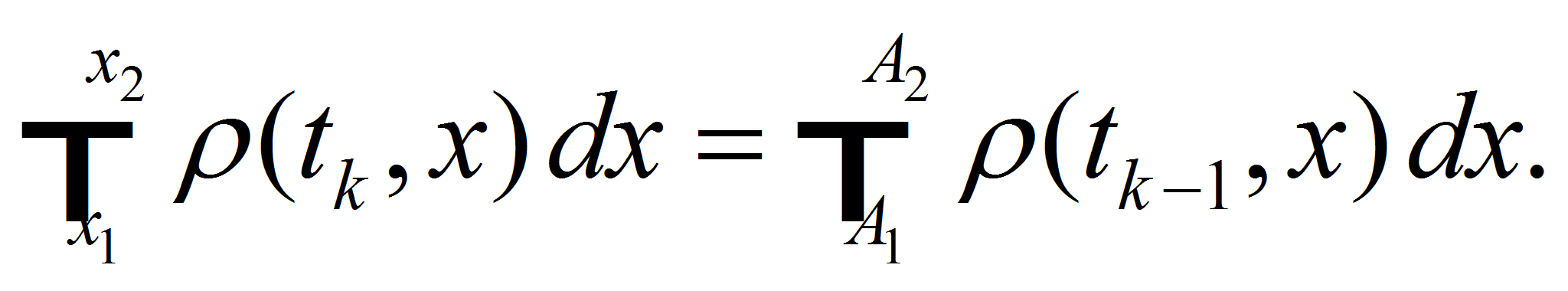(4)

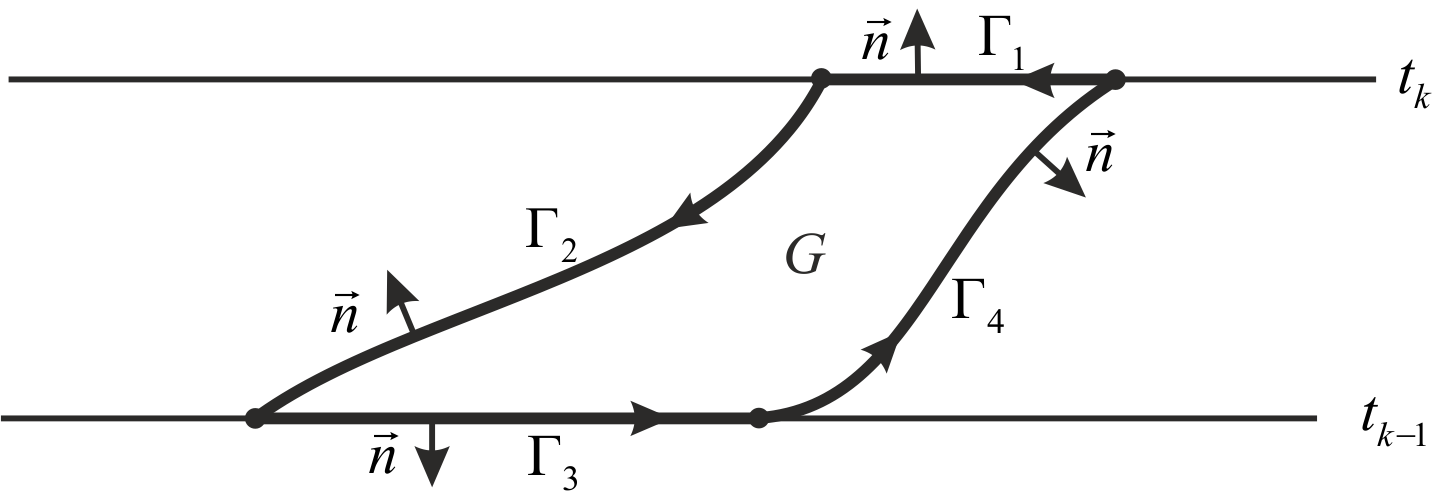
Proof. Define by 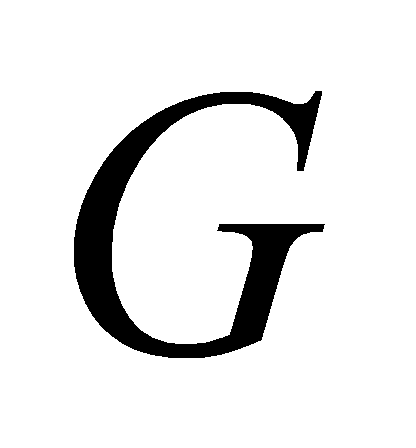the curvilinear quadrangle bounded by lines 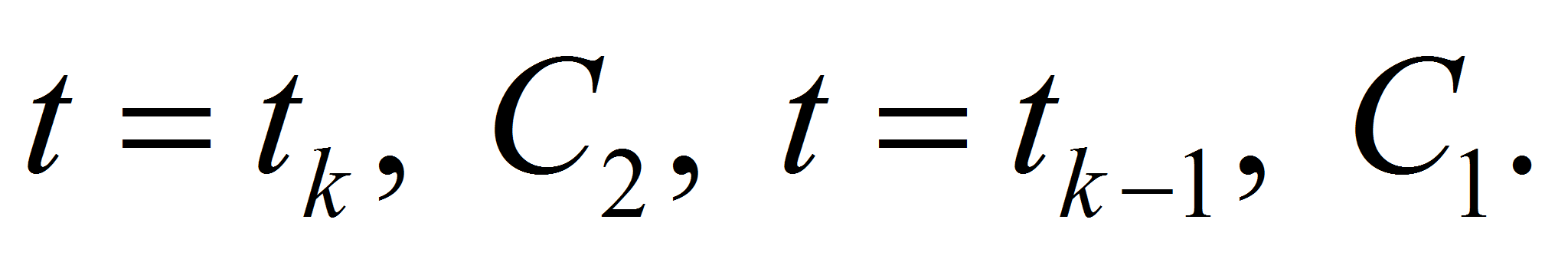And define by 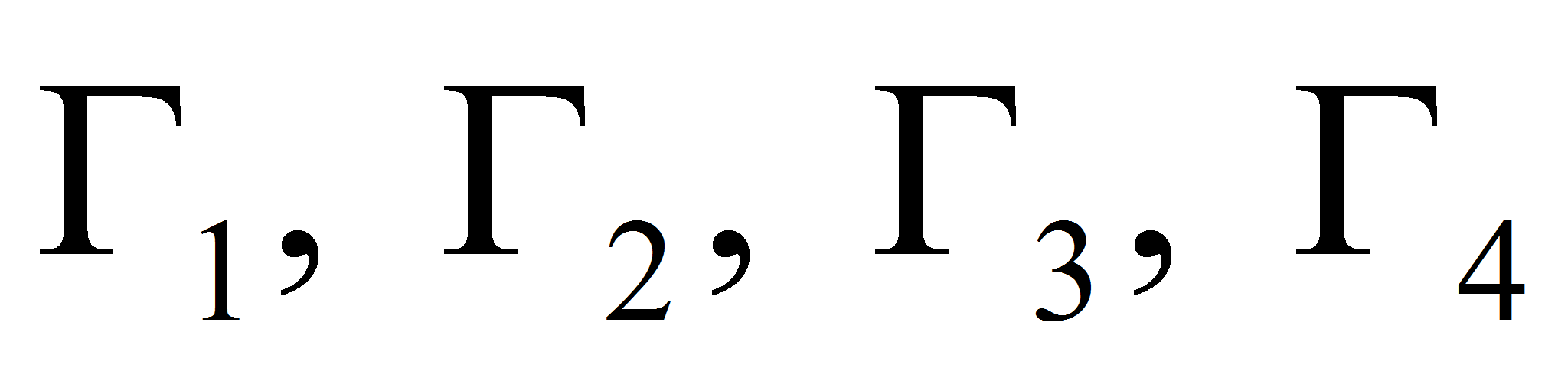the corresponding parts of these lines, which form the boundary 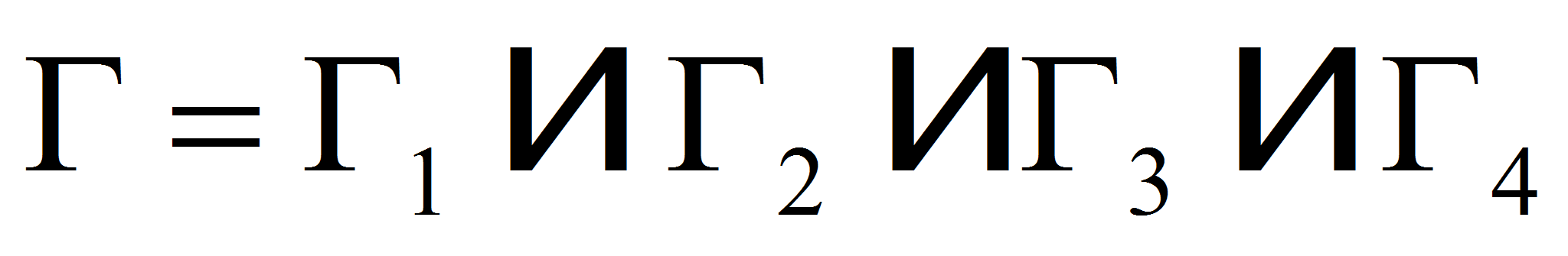(see Fig. 2). Introduce also the external normal defined at each part of boundary except 4 vertices of quadrangle.

Now use formula by Gauss-Ostrogradskii [16, 17] in the following form:

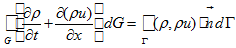(5)

where sing means scalar product. Since the boundary 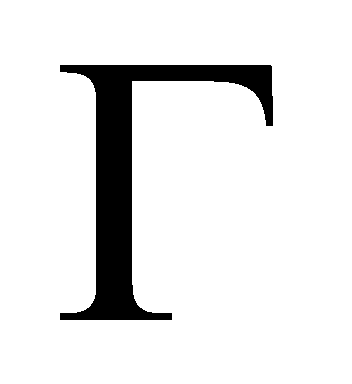consists of four parts we calculate the integral over 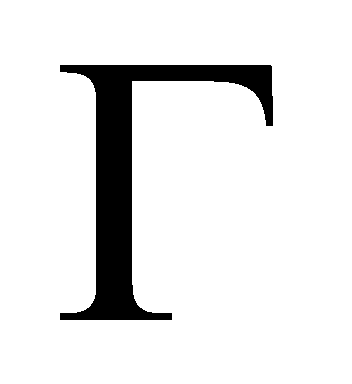separately on each line:

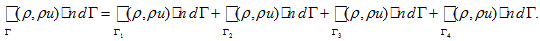(6)

Fig. 2. Integration along boundary

Along the line 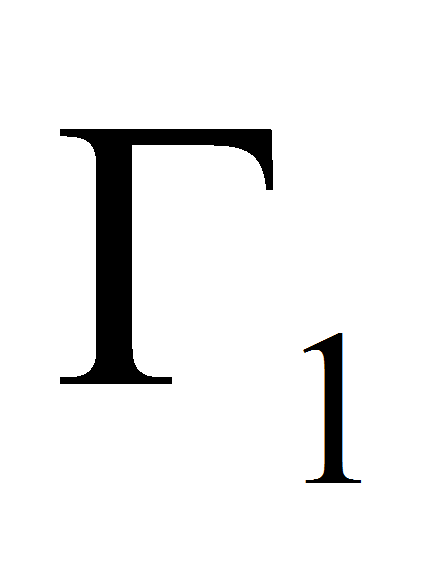the external normal equals 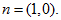Then

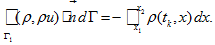(7)

Minus appeared in right-hand side because of opposite direction of integration. At arbitrary point the tangent vector is Therefore the external normal equals

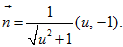(8)

Therefore we get

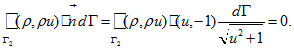(9)

For other two parts of the boundary we use the same way to calculate the integrals and get

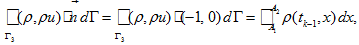(10)

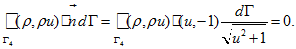(11)

Combine (5) — (7) and (9) — (11):

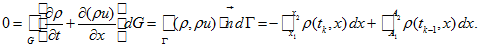
It implies (4). □

3. Simple semi-discrete approximation

Now take integer 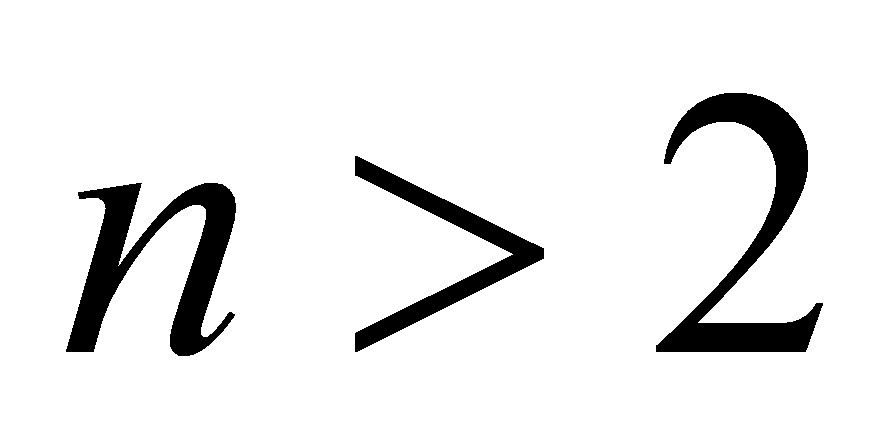and construct uniform mesh in with nodes 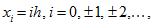and meshsize 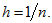Let we know the (approximate) solution 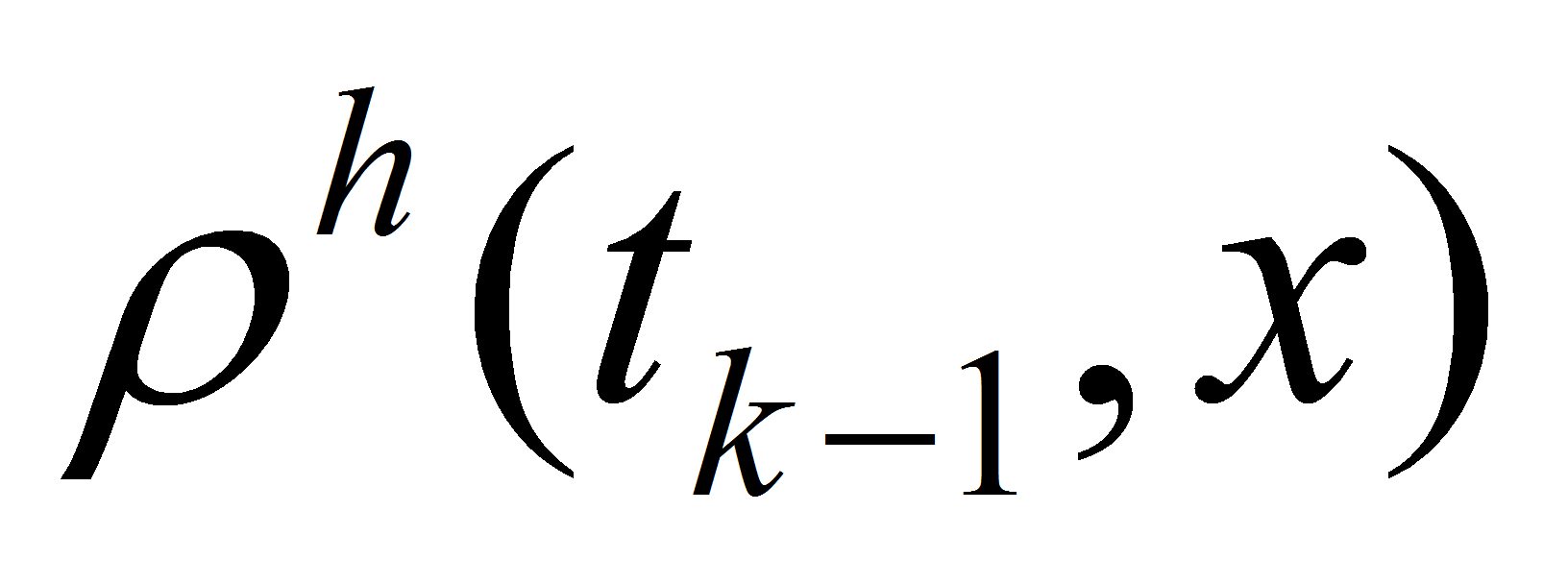at time level 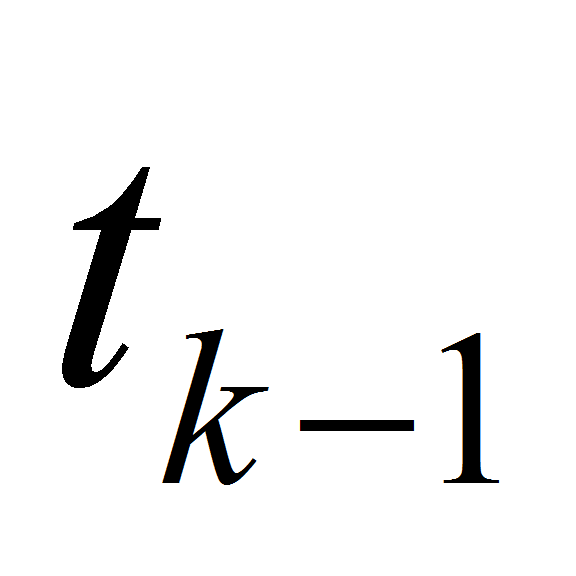and construct the approximate solution at time level 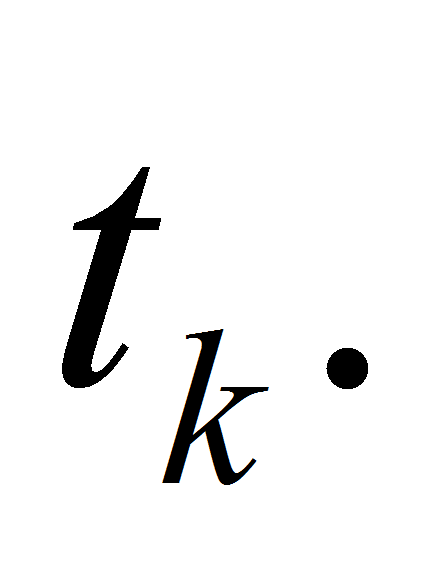Integrals of solution in a small vicinities of each point 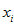may be some useful intermediate data. For example, let construct integrals

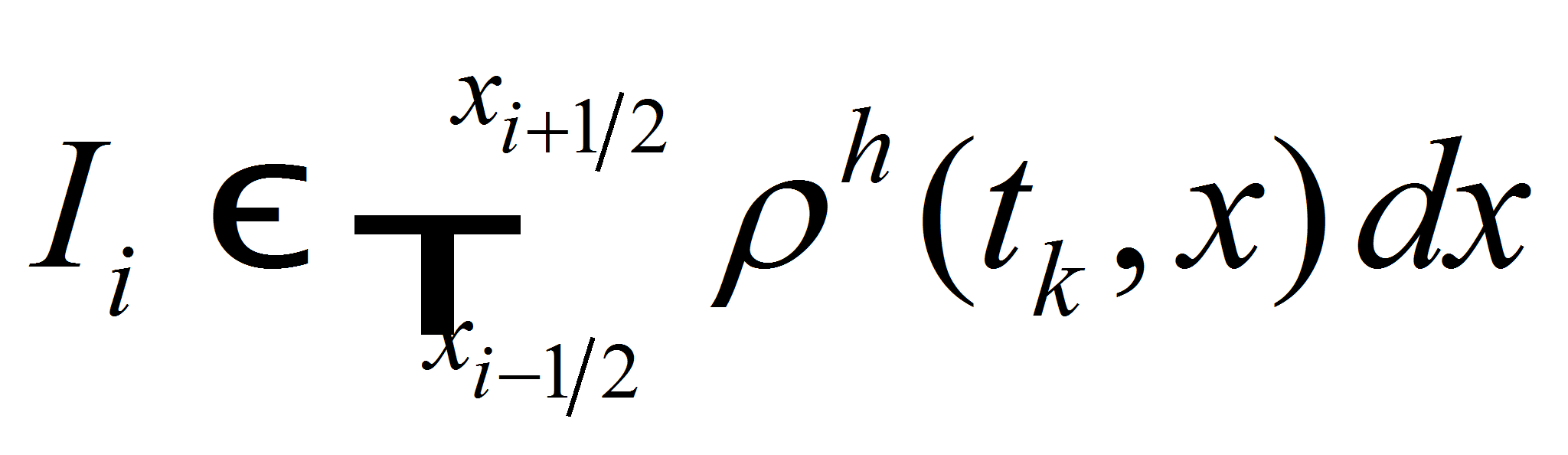(12)

at each interval

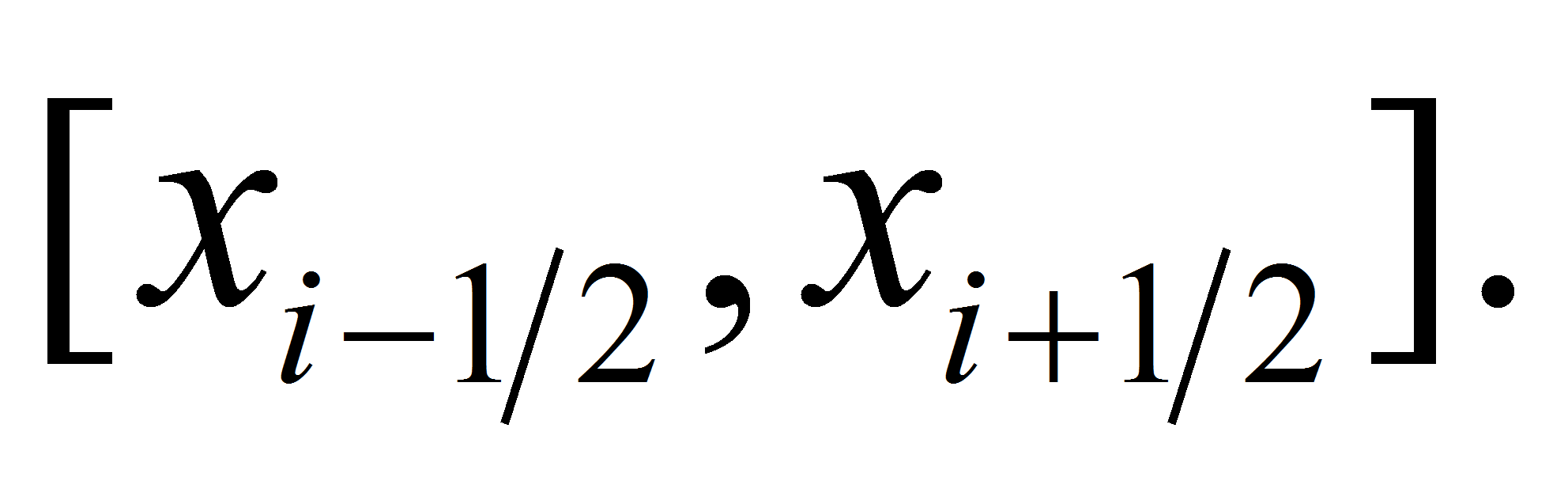
For this purpose in the context of previous section we take two points 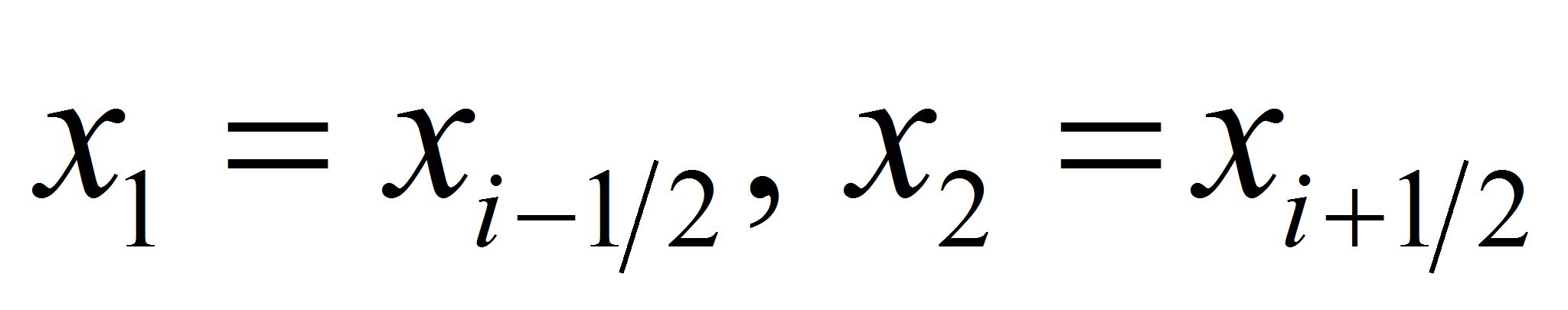and construct two trajectories These trajectories produce two points 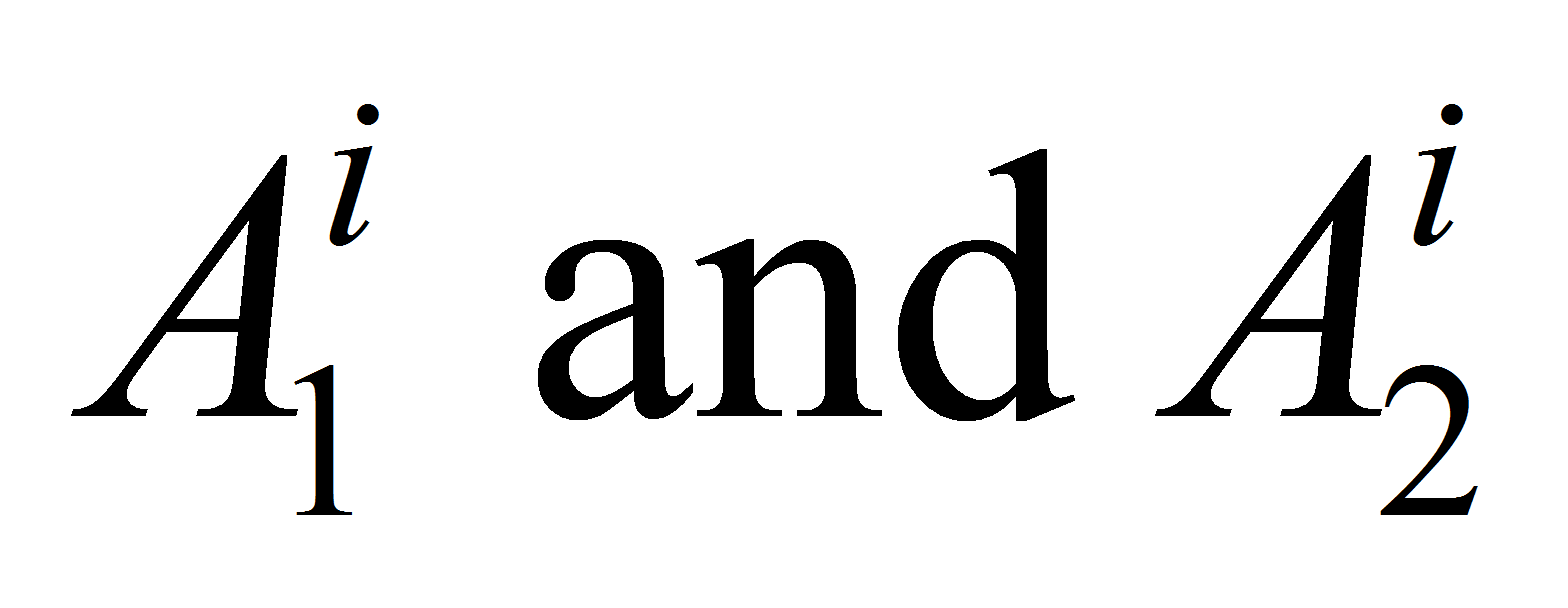at time level 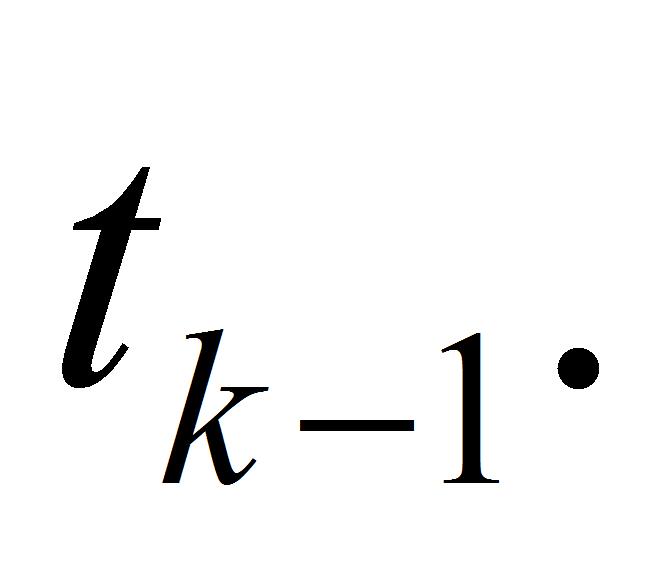Due to Theorem 1 we get

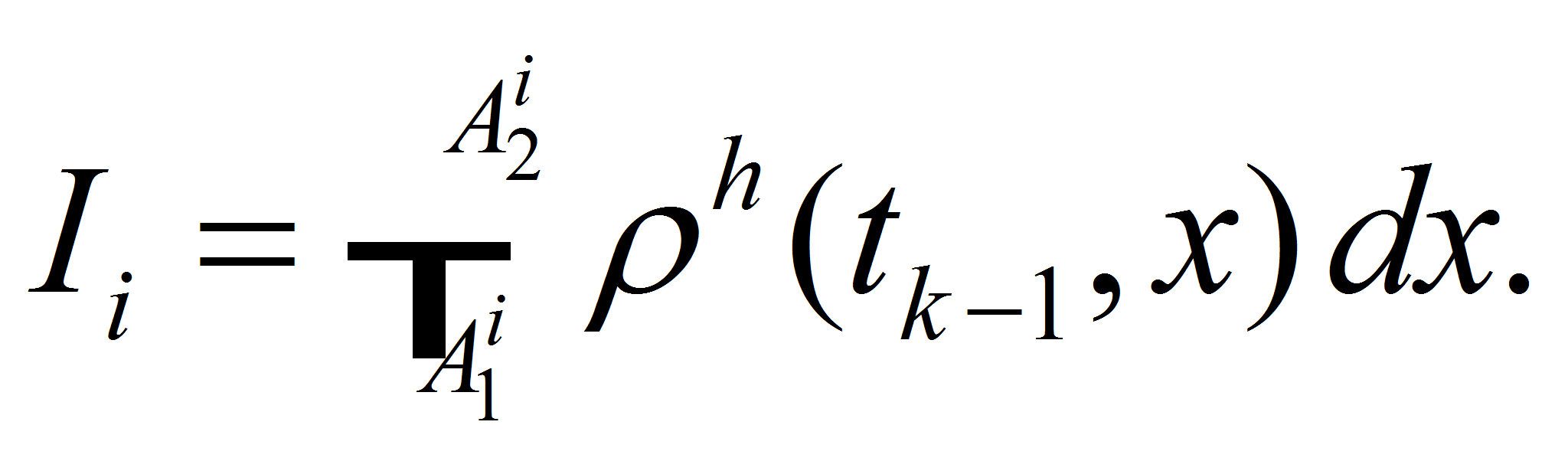(13)

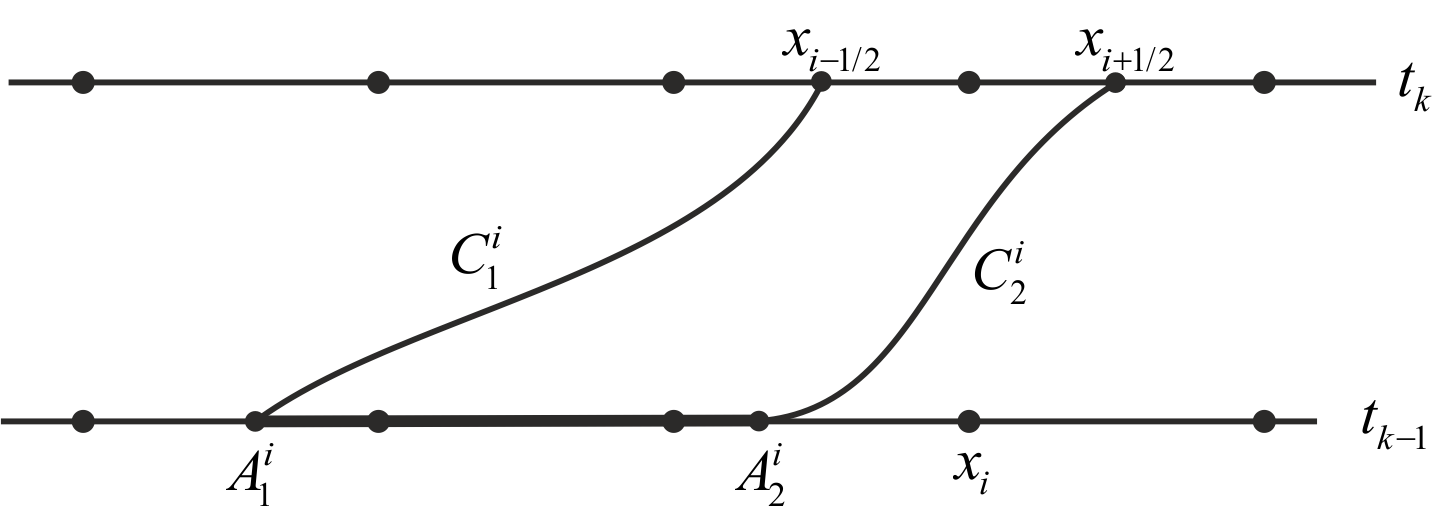
Fig. 3. Segment for partial integration on grid

But at previous level we know only integrals on segment which generally do not coincide with segment 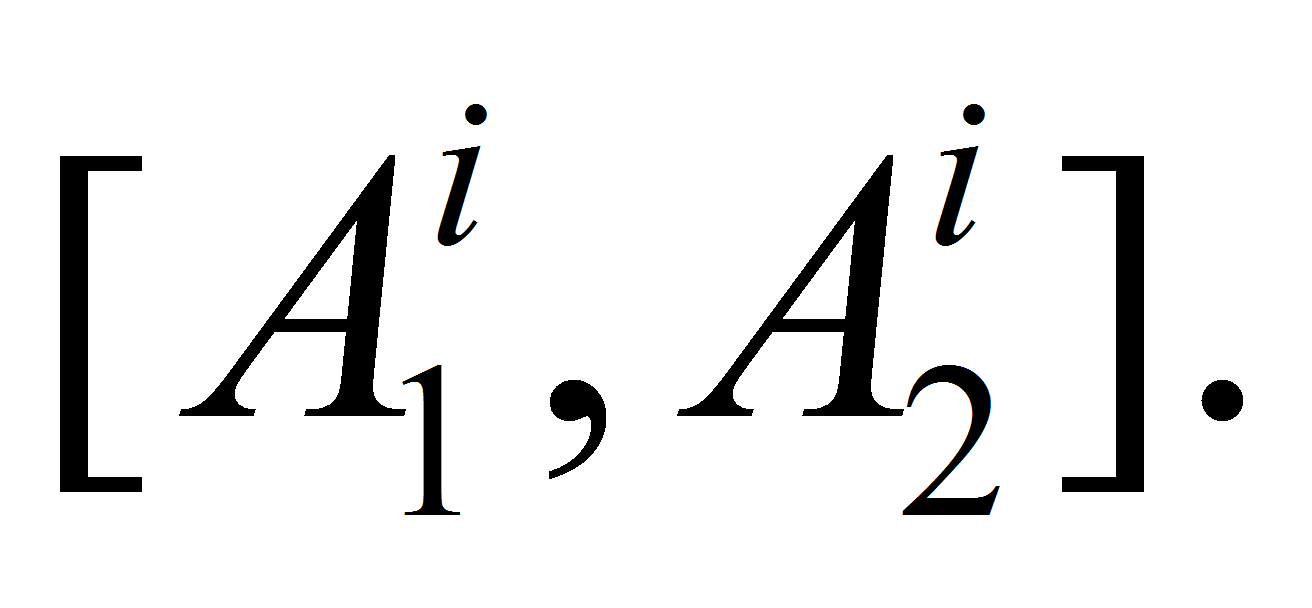For example, let we have situation at level 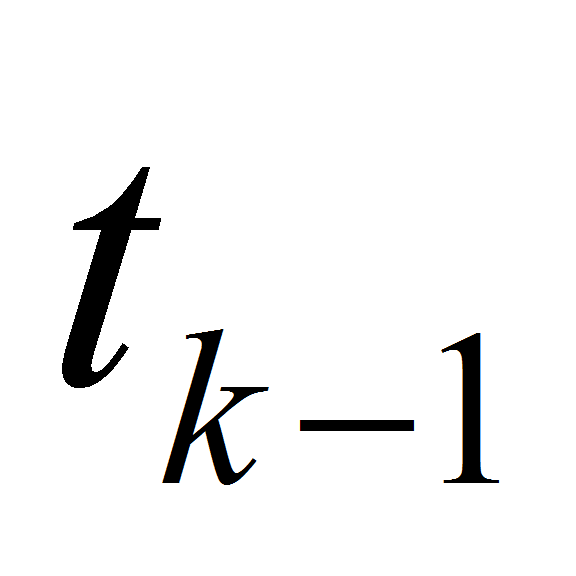with some integer 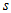as in Fig. 3. So, we need to use some approximation of partial integrals.

The simple way consists in approximation of solution by piece-wise constant function. Thus we put

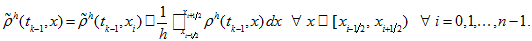(14)

But this interpolation is rather rough. It gives accuracy of order 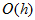only. Instead of it we take linear interpolation at each segment 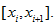For this purpose at first we put

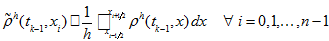(15)

and then define

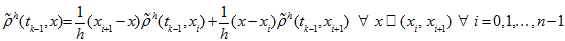(16)

with period 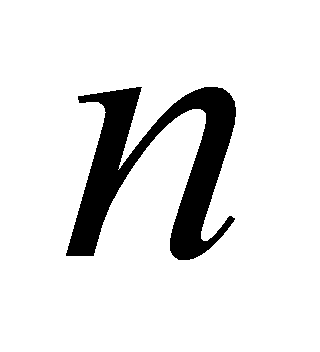for 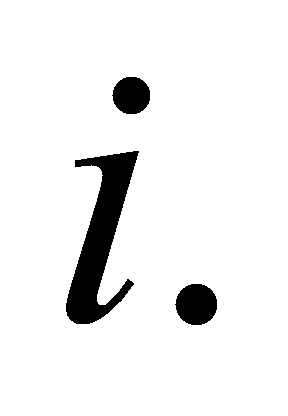This time we get interpolation accuracy of order

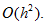
Of course the situation at initial level 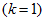is simpler: we can use for example trapezoidal quadrature formula for any segment 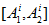with accuracy

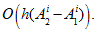
Therefore our numerical algorithm for solving problem (1) — (2) is as follows. Take integer 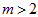and construct uniform mesh in 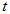with nodes 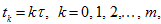and meshsize 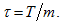Then for 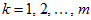make the following cycle supposing that the approximate solution 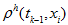is known yet at previous time-level for

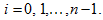
1. With the help of values in these points and periodicity we construct the piecewise linear (periodical) interpolant

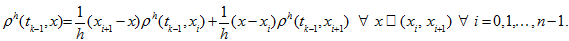(17)

2. For each point 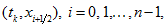construct trajectories 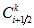down to time-level 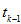like in previous considerations. They produce cross-points 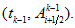If 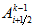goes outside segment 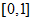we use periodicity of our data.

2. For each interval 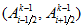compute integral

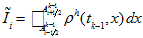(18)

by trapezoid quadrature formula separately at each nonempty subinterval 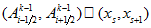where 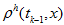is linear.

3. Due to Theorem 1 it is supposed that

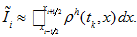(19)

Therefore like in (15) — (16) we put

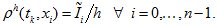(20)

Thus, we complete our cycle which may be executed up to last time-level

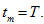
Condensed form of this algorithm in terms of piecewise linear periodical interpolants is written as follows:

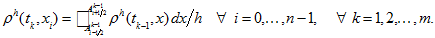(21)

So, we get approximate discrete solution 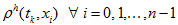at each time-level 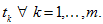First we prove the conservation law in discrete form.

Let a discrete function 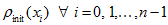is given, and we construct piecewise linear interpolant 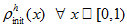with period 1.

Theorem 2. For any initial condition 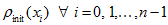the approximate solution (17) — (20) 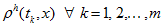satisfies the equality:

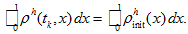(22)

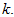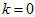Proof. We prove this equality by induction in For this inequality is valid because of initial condition. Suppose that estimate (21) is valid for some 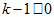and prove it for 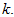Indeed, because of (18) and (20) we get

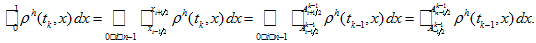
And due to periodicity of function

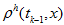
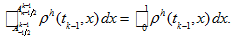
Thus we prove

□

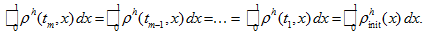Now we prove a stability of algorithm (17) — (20) in the discrete norm analogous to that of space

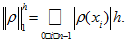(23)

Theorem 3. For any intermediate discrete function 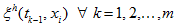the solution 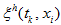of (17) — (20) satisfies the inequality:

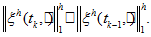(24)

Proof. Indeed, because of (18) and (20) we get

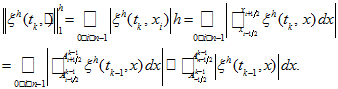(25)

Due to periodicity of functions 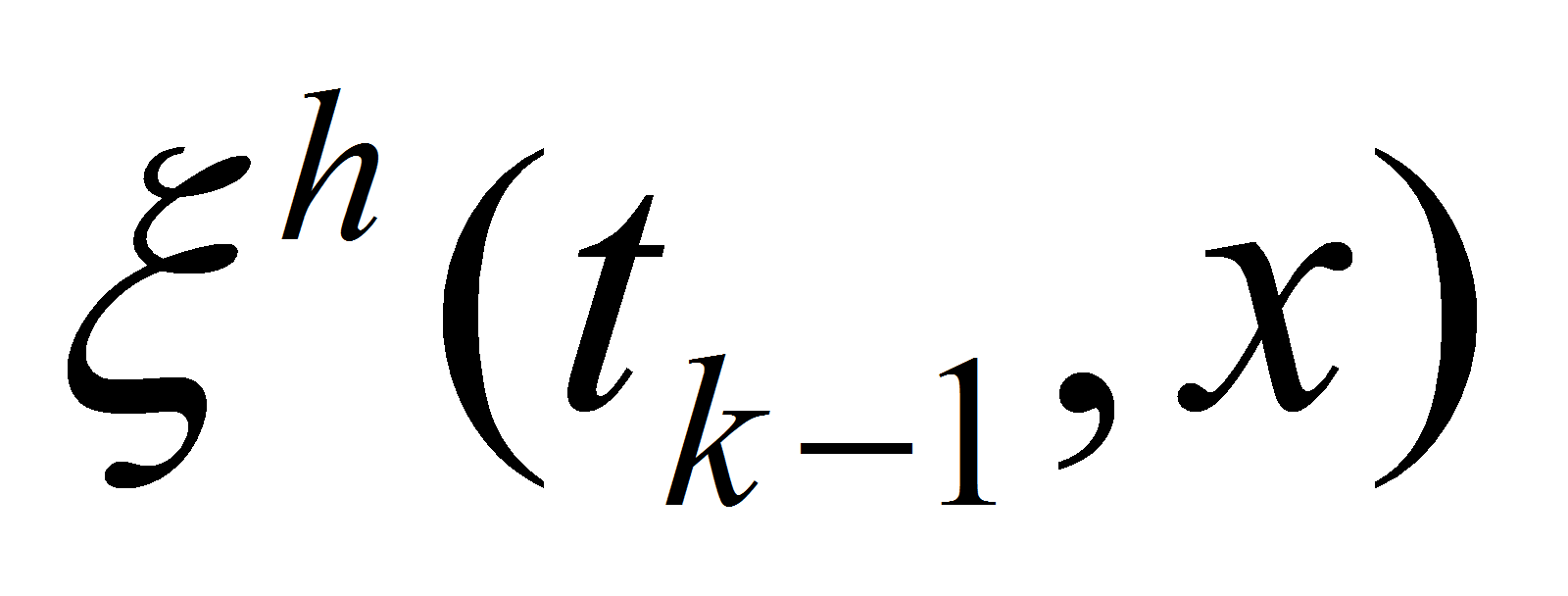and

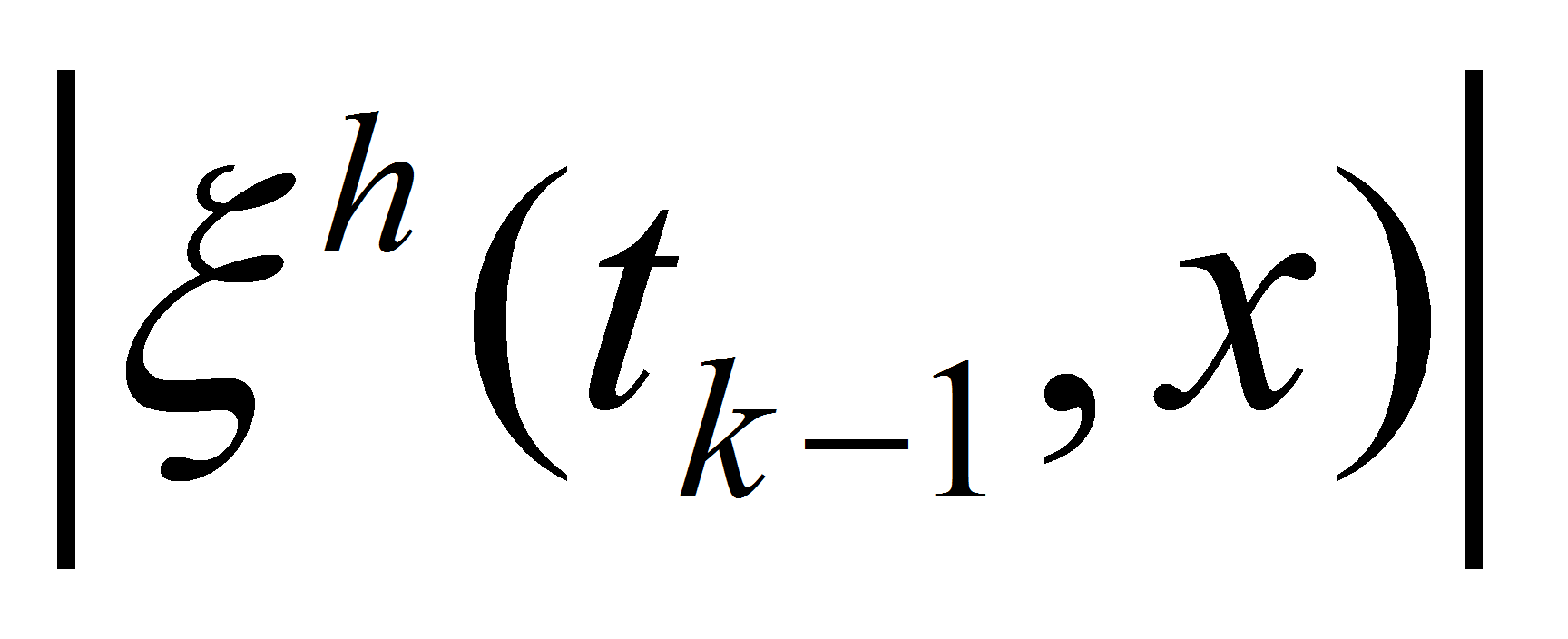
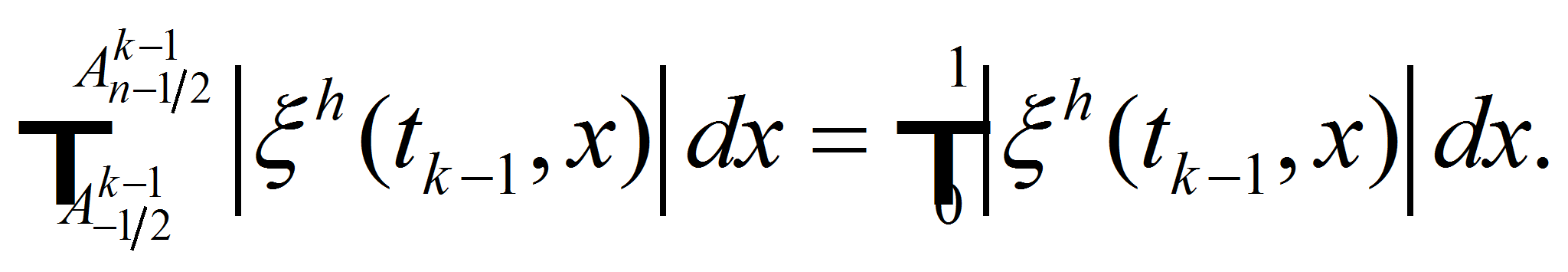(26)

Let introduce the basis functions for linear interpolation

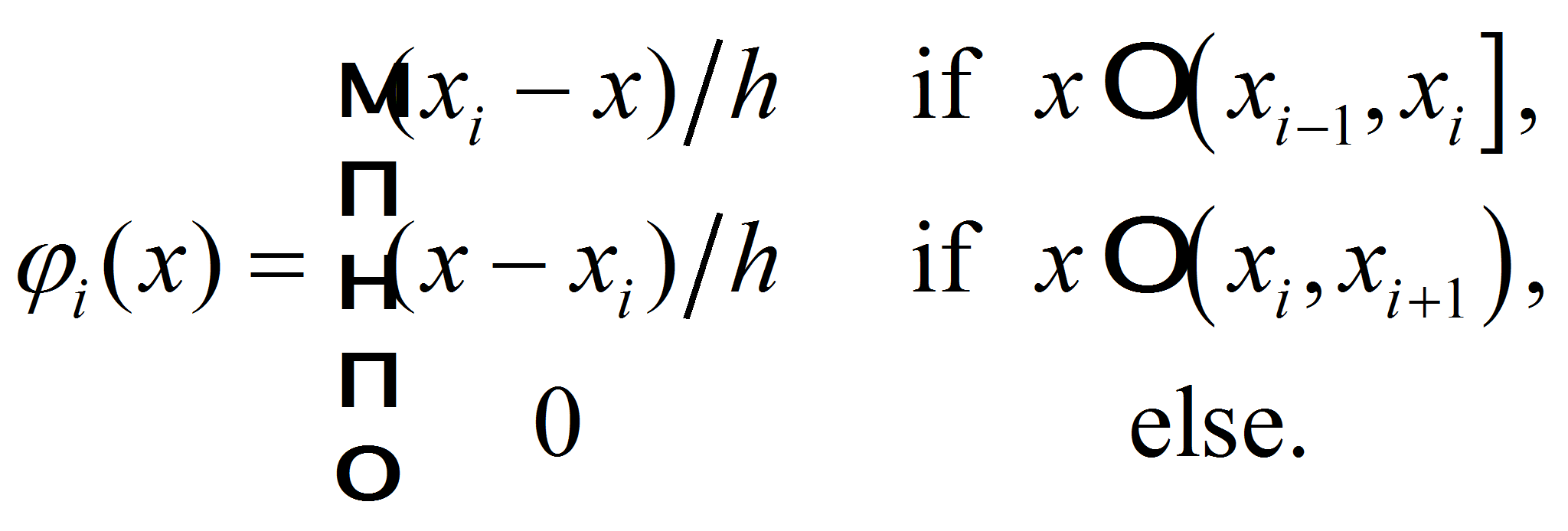
Then for piecewise linear interpolant we get

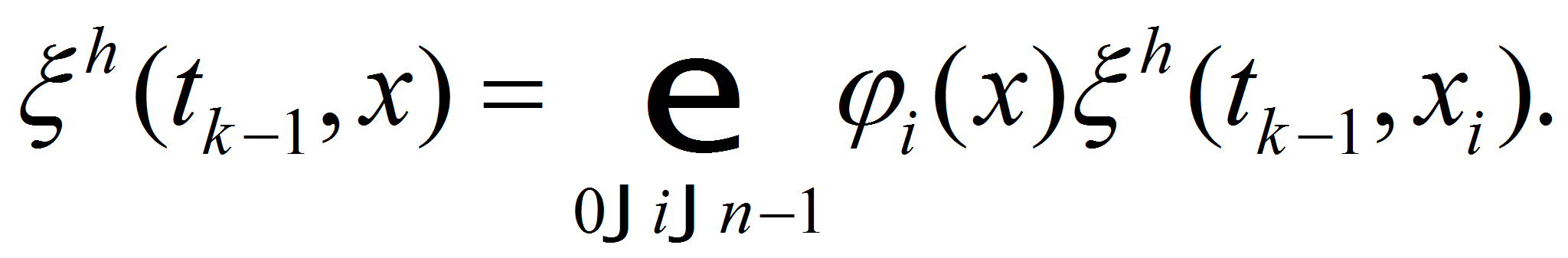
Then

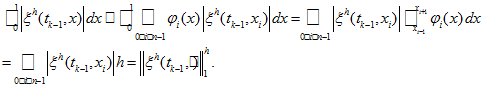
Combine this inequality with (25) and (26) we get (24). □

Now evaluate an error of approximate solution in introduced discrete norm.

Theorem 4. For sufficiently smooth solution of problem (1) — (2) we have the following estimate for the constructed approximate solution:

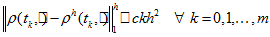(27)

with a constant 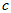independent of

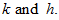
Proof. We prove this inequality by induction in 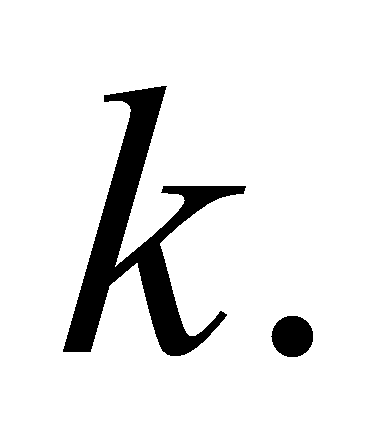For 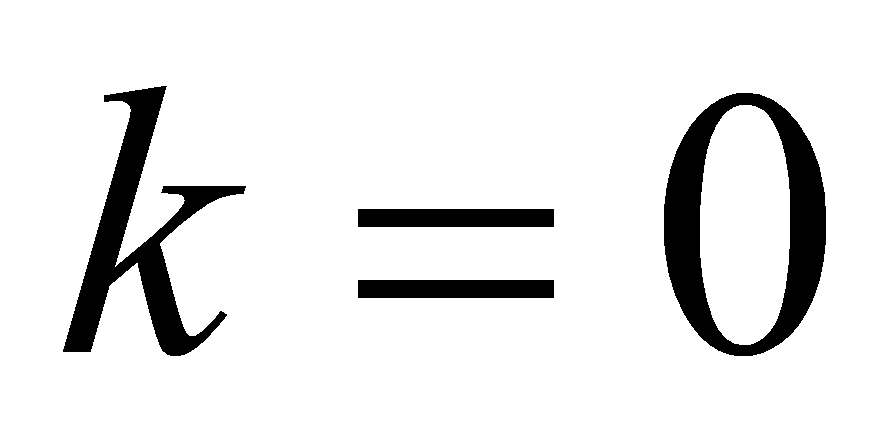this inequality is valid because of exact initial condition (2): 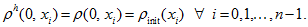Suppose that estimate (26) is valid for some 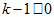and prove it for

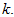
So, at time-level 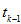we have decomposition

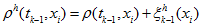(28)

with a discrete function 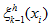that satisfies the estimate

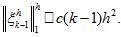(29)

Because of Taylor series in 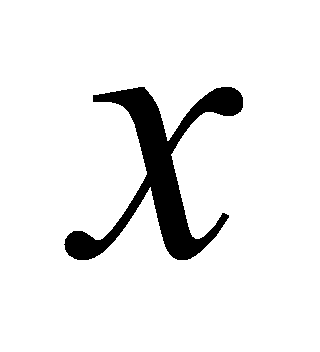of 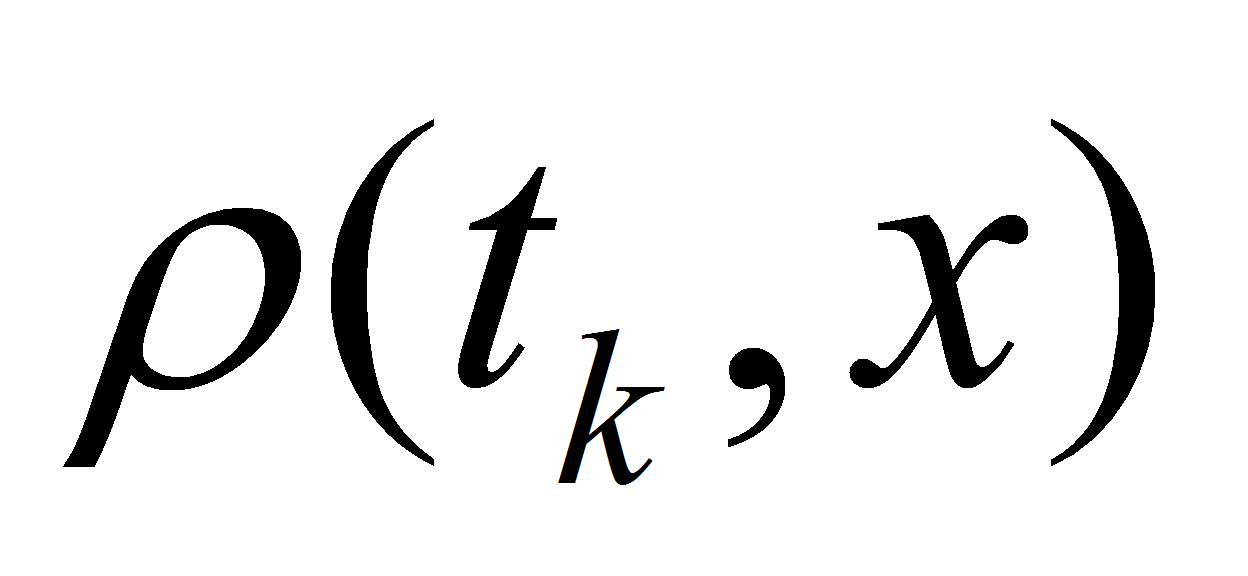in the vicinity of point 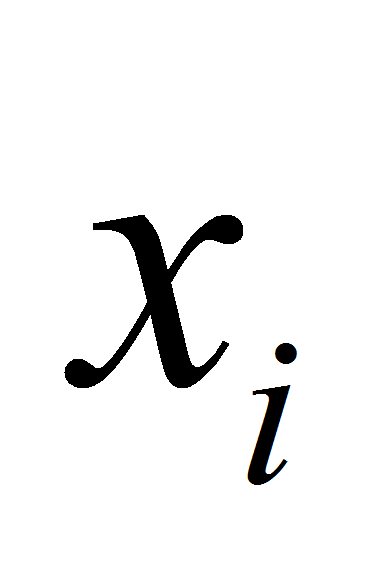we get equality

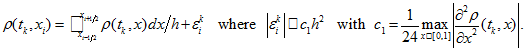(30)

Because of Theorem 1

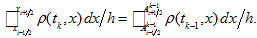
Instead of 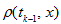let use its piecewise linear periodical interpolant 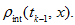Then

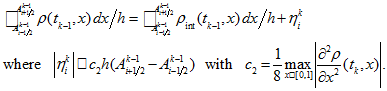(31)

Thus, we get equality

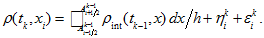(32)

For 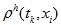we use (21) and (28):

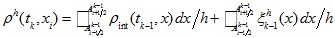(33)

where values of 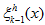are constructed by piecewise linear periodical interpolation.

Now let subtract (33) from (32), multiply its modulus by 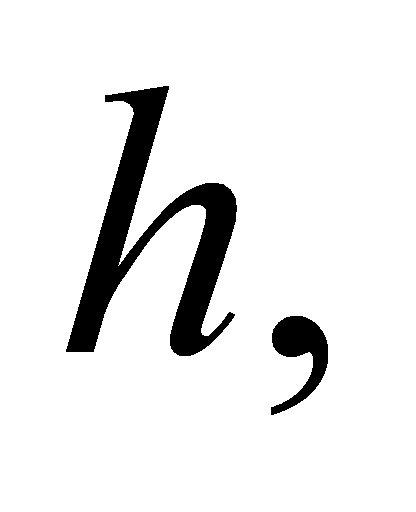and sum for all

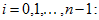
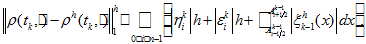(34)

Due to Theorem 3 last terms in brackets is evaluated by 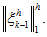Thus

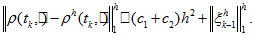(35)

Let put 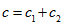then this inequality is transformed with the help (29):

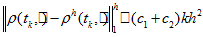
that is equivalent to (27). □

We can see that at last level we get inequality

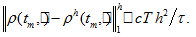(36)

In some sense we got a restriction on temporal meshsize to get convergence. For example, to get first order of convergence, it is enough to take

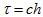
with any constant 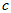independent of 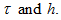But this restriction is not such strong up to constant as Courant — Friedrichs — Lewy (CFL) condition:

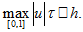(37)

Moreover, it is opposite in meaning: here the greater 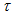the better accuracy.

Thus, this approach is convenient for the problems with huge velocity 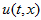which come from a computational aerodynamics: we have computational stability on the base of Theorem 3 and conservation law on the base of Theorem 2.

4. Numerical experiment

Let take 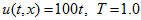and solve this equation with initial condition

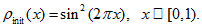
Then exact solution is

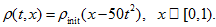
The result of implementing the presented algorithm is given in Table 1 for several 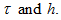The first column of Table 1 expresses a relation 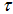/ h (for most implemented values in computations) and the first string shows a number n of mesh nodes. Other entries contain the value

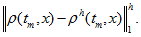
Table 1

Thus we indeed have the first order of accuracy on h when 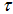/ h is fixed.

5. Conclusion

Thus, we present the numerical approach which is more convenient for huge vel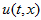ocity then approaches listed in introduction. Of course, we stay some open questions like boundary condition instead of periodical one, nonlinear dependence of velocity 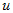on solution 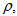and other. Of course, we need to trace the effect of the approximate solving the characteristics equations instead of exact process. But we successively consider these issues in next publications, including generalization for two-dimensional and three-dimensional equations.

At first glance, this approach is some integral version of the characteristics method. Moreover, its accuracy is higher, the less time steps done in the algorithm. But in the future, we will apply it to the equations with nonzero right-hand side for the approximation of which a small time step 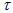will be crucial.

References:

1. Harten A.: On a class of high resolution total-variation-stable finite-difference schemes // SIAM J. Numer. Anal. — 1984. — V. 21. — P. 1–23.
2. Harten A., Osher S.: Uniformly high-order accurate non-oscillatory schemes // I. SIAM J. Numer. Anal. — 1987. — V. 24. — P. 279–309.
3. Harten A., Engquist B., Osher S., Chakravarthy S.: Uniformly high-order accurate non-oscillatory schemes, III // J. Comput. Phys. — 1987. — V. 71. — P. 231–303.
4. Osher S.: Convergence of generalized MUSCL schemes // SIAM J. Numer. Anal. — 1985. — V. 22. — P. 947–961.
5. Osher S., Chakravarthy S.: High-resolution schemes and entropy condition // SIAM J. Numer. Anal. — 1984. — V. 21. — P. 955–984.
6. Osher S., Tadmor E.: On the convergence of different approximations to scalar conservation laws // Math. Comput. — 1988. — V. 50. — P. 19–51.
7. Sanders R.: A third-order accurate variation nonexpansive difference schem for single nonlinear conservation laws // Math. Comput. — 1988. — V. 51. — P. 535–558.
8. Чирков Д. В., Черный С. Г.: Сравнение точности и сходимости некоторых TVD-схем // Вычислительные технологии. — 2000. — Т. 5, № 5. — С. 86–107.
9. Cockburn B., Shu C.-W.: TVB Runge-Kutta projection discontinuous Galerkin finite element method for conservation laws II: general framework // Math. Comput. — 1988. — V. 52. — P. 411–435.
10. Shu C.-W.: TVB uniformly high-order schemes for conservation laws // Math. Comput. — 1987. — V. 49. — P. 105–121.
11. Shu C.-W.: TVB boundary treatment for numerical solution of conservation laws // Math. Comput. — 1987. — V. 49. — P. 123–134.
12. Shu C.-W.: Total-Variation-Diminishing time discretizations // SIAM J. Sci. Statist. Comput. — 1988. — V. 9. — P. 1073–1084.
13. Shu C.-W., Osher S.: Efficient implementation of essentially non-oscillatory shock-capturing schemes // J. Comput. Phys. — 1988. — V. 77. — P. 439–471.
14. Sweby P.: High-resolution schemes using flux limiters for hyperbolic conservation laws // SIAM J. Numer. Anal. — 1984. — V. 21. — P. 995–1011.
15. Shaydurov V., Liu T., Zheng Z.: Four-stage computational technology with adaptive numerical methods for computational aerodynamics // American Institute of Physics. Conference Proceedings. — 2012. — Vol. 1484. — P. 42–48.
16. Streeter V. L., Wylie E. B.: Fluid mechanics. — London: McGraw-Hill. — 1998.
17. Polyanin A. D.: Handbook of linear partial differential equations for engineers and scientists. — Boca Raton: Chapman & Hall/CRC Press. — 2002.