В статье определен алгоритм реализации метода минимизации конечного автомата для оптимального сжатия телеметрической информации, передаваемой с автономного технического средства по радиоканалам, путем представления телеметрической информации в форме состояний конечного автомата. Результат использования данного алгоритма позволяет в равной степени актуальности и достоверности получать любой вид телеметрической информации с автономного технического средства, освобождая дополнительное место в канале передаче информации.
Ключевые слова: сжатие информации, автономное техническое средство, телеметрическая информация, конечный автомат.
Постоянный рост объемов телеметрической информации (далее — ТМИ) в автономных технических средствах приводит к сложности оперативной обработки данных. Появляется необходимость разработки новых требований к процессу сжатия информации. Для сжатия телеметрической информации, как правило, применяют алгоритмы, обеспечивающие точное восстановление исходных данных с целью их дальнейшей обработки и анализа. Телеметрические данные, передаваемые с датчиков и устройств на пункт обработки, могут быть представлены в форме текста, изображений, аудио и различных других форматах. Сжатие этих данных позволяет эффективно использовать пропускную способность во время передачи потока информации и уменьшает ресурсы хранения пункта обработки. Однако, при разработке устройств и алгоритмов, проводящих сжатие ТМИ, требуется учитывать ширину канала передачи информации, а также обращать внимание на большую избыточность передаваемой информации. В системах с циклической дискретизацией избыточность данных возникает даже при правильно выбранной частоте опроса датчиков, так как при мало меняющихся во времени параметрах частота опроса остается той же, что и на участках, где такая частота является необходимой. Таким образом, целью сжатия данных является формирование минимального количества информации, обеспечивающей воспроизведение первичного сигнала с заданной вероятностью [1].
В последние годы разработано множество методов сжатия информации, используемых для передачи информации разного представления. Подробный анализ данных методов представлен в таблице 1 [2].
Таблица 1
|
№ п/п |
Наименование метода |
Достоинства |
Недостатки |
|
1. |
Метод экстраполяции |
Наиболее помехоустойчив к воздействию потенциального противника. Коэффициент сжатия около 70 процентов. |
Сжатие требует запоминание последнего существенного отсчета. |
|
2. |
Метод адаптивной дискретизации |
Позволяет уменьшить среднюю частоту дискретизации. Точка опроса не образует периодической последовательности. |
Необходимо передавать дополнительную информацию в виде значений времени появления существенных выборок. |
|
3. |
Метод интерполяции |
Позволяет исключить большее число избыточных отсчетов. |
Величина коэффициента сжатия зависит от ширины апертуры. |
|
4. |
Метод автоматической регулировки частоты опроса сигнала |
Можно передавать данные, занимающие полосу 80 кГц в реальном масштабе времени в полосе канала 3,2 кГц. |
Сложность реализации алгоритмов сжатия данных. |
Проанализировав методы сжатия, используемые для передачи ТМИ, можно сделать вывод, что все указанные в таблице 1 методы сжатия информации имеют существенные недостатки, присутствие которых не гарантирует достоверности и актуальности переданной ТМИ с автономного технического средства. Это объясняется необходимостью использовать достоинства того или иного метода сжатия данных при выполнении конкретной задачи, что уменьшает универсальность.
При эксплуатации автономных технических средств требуется передача наиболее актуальной и достоверной ТМИ. Актуальность должна достигаться путем сокращения объема передаваемой ТМИ в канале передачи данных. Достоверность должна достигаться путем создания универсальных алгоритмов обработки получаемой информации на пункте обработки.
Таким образом, использование каждого метода по отдельности несет потери в том или ином качестве получаемой ТМИ. Предлагается рассмотреть передаваемую информацию как набор состояний конечного автомата.
С практической точки зрения ТМИ с автономного технического средства представляет собой набор состояний конечного автомата. Интерес здесь представляет только зависимость между входами и выходами автомата, а роль его состояний сводится исключительно к участию в формировании этих зависимостей в качестве промежуточных переменных. Следовательно, любая совокупность состояний, обеспечивающая требуемые зависимости между входом и выходом, может быть выбрана в качестве множества состояний автомата. В то же время этот выбор естественно подчиняется определенным целям, например, минимизации числа состояний или оптимизации автомата. Следует иметь ввиду, что с уменьшением числа состояний уменьшается и количество требуемых элементов памяти, но это может привести к усложнению комбинационной схемы автомата. Поэтому синтез наиболее экономичного автомата часто требует поиска удачного компромисса между сложностью его комбинационной и запоминающей частей.
Алгоритм сжатия ТМИ должен обладать свойством биекции, т. е. быть одновременно инъективным (однозначное соответствие между множествами зависимостей конечного автомата) и сюръективным, следовательно, алгоритм должен обладать взаимно однозначным соответствием между зависимостями конечного автомата.
На рис. 1а, 1б и 1в представлены графические изображения соответственно инъекции, сюръекции и биекции [3, 4].

а

б

в
Рис. 1. Графическое изображение свойств биекции
Пусть
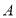
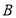
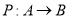
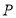
Отображение множества телеметрических датчиков на множество наименований этих датчиков является сюръекцией, поскольку все датчики имеют названия и каждое название является названием того или иного телеметрического датчика.
Соответствие между элементом множества телеметрических датчиков заводскому номеру этого датчика является биекцией [5].
Выше рассмотрены отображения множеств без учета того, что между элементами отображаемых множеств могут быть определены отношения. Отображения множеств, на которых заданы отношения, представляют интерес как преобразования структур.
Задан автомат
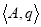
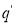
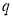
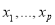
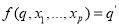
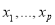
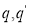
Состояние
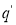
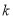
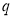
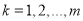
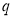
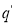
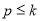
Если
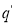
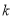
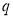
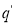
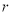
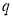
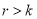
Если
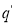
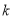
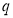
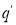
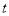
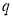
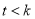
Допустим, что задан автомат
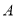
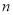
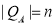
Пусть
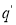
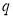
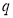
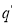
Этот фрагмент последовательности можно удалить и последовательность все равно будет достижимой для
q
i
и
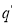
Если состояние
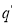
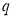
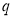
Соответственно, если
q
ў (
n
-1)-недостижимо из
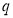
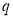
Входная последовательность
x
1
…
x
p
задает обход состояний автомата
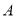
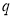
Состояния
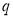
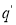
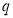
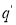
Состояния
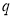
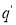
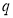
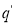
Если состояния
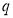
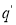
Состояния
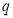
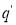
Состояния
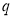
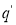
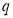
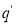
Если состояния
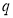
С практической точки зрения интерес представляет только зависимость между входами и выходами автомата, а роль его состояний сводится исключительно к участию к формированию этих зависимостей в качестве промежуточных переменных.
Следовательно, любая совокупность состояний, обеспечивающая требуемые зависимости между входом и выходом, может быть выбрана в качестве множества состояний автомата [6].
В то же время этот выбор естественно подчинить определенным целям, например, минимизации числа состояний или оптимизации автомата в каком-либо смысле. Следует иметь в виду, что с уменьшением числа состояний уменьшается и количество требуемых элементов памяти, но это может привести к усложнению комбинационной схемы автомата. Поэтому синтез наиболее экономичного автомата часто требует поиска удачного компромисса между сложностью его комбинационной и запоминающей частей.
Минимизация числа состояний автомата связана с анализом эквивалентности его состояний.
Пусть задан некоторый автомат А с n состояниями. Сопоставим автомату А автомат В следующим образом. Пусть X B = X A , Y B = Y A , т. е. множества входных и выходных переменных (алфавиты входных и выходных символов) автоматов А и В совпадают.
Множество состояний Q B = P n -2 , где P n -2 = { S 1 ,..., S r } — множество классов ( n -2)-эквивалентности, образованное из множества Q А , |P n -2 | Ј |Q А | = n . Функция выходов j В ( S i ) = j А ( q ), если q О S i . Функция переходов f B ( x , S i ) = S j , если при q О S i f А ( x , q ) = q ўО S j .
Построенный таким образом автомат В называется минимальной формой автомата А , а автомат В имеет минимальное число состояний среди эквивалентных автоматов автомату А .
Минимальная форма автомата А является приведенным автоматом.
[7] Пусть задан автомат А с четырьмя состояниями, т. е. n = 4,|Q| = 4 (Рис. 2).
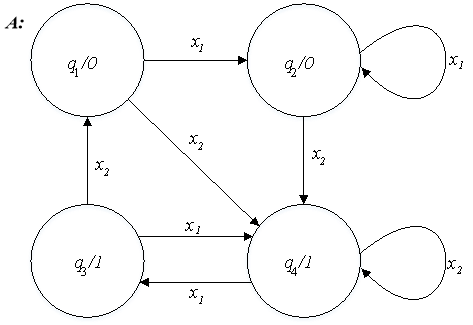
Рис. 2. Конечный автомат А
Произведем анализ эквивалентности состояний автомата А .
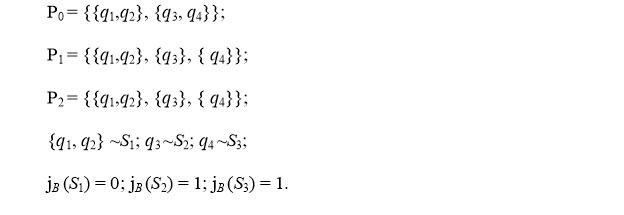
Отсюда автомат В , являющийся минимальной формой автомата А , т. е. являющийся эквивалентным автомату А с минимальным числом состояний, будет выглядеть следующим образом (Рис. 3):
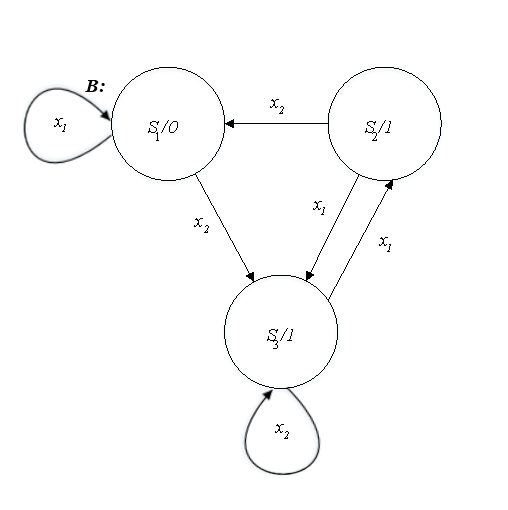
Рис. 3. Автомат В — минимальная форма автомата А
Исходя из полученного анализа алгоритм преобразования конечного автомата можно представить следующим образом (Рис. 4):
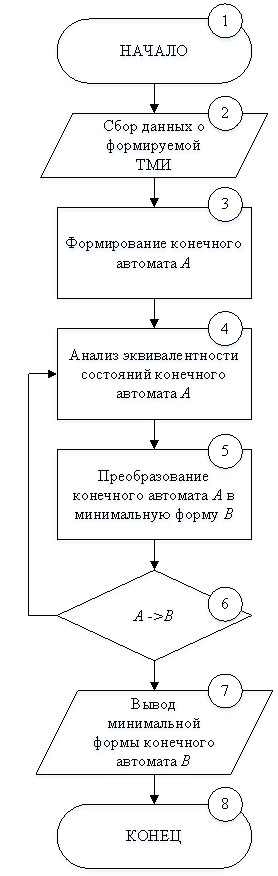
Рис. 4. Алгоритм сжатия ТМИ путем автоматного представления данных
Литература:
- Верба В. С., Меркулов В. И., Попов Е. В., Чернов В. С. Интеграция данных в многодатчиковых бортовых информационно-управляющих системах. — Информационно-измерительные и управляющие системы, 2014.
- Симонович С. В. Информатика. — СПб.: Питер, 2008.
- Вернер М. Основы кодирования — М.: Техносфера, 2004.
- Сэломон Д. Сжатие данных, изображение и звука — М.: Техносфера, 2006.
- Сергеев В. В. Анализ и обработка изображений, получаемых при наблюдениях земли из космоса. — Компьютерная оптика, 2006.
- Эльшафеи М. А., Сидякин И. М., Харитонов С. В., Ворнычев Д. С. Исследование методов обратимого сжатия телеметрической информации. — Вестник МГТУ им. Н. Э. Баумана. Сер. «Приборостроение», 2014.
- Чье Ен Ун, Левенец А. В., Нильга В. В. Представление телемеханических данных однородными n-мерными структурами как предварительная обработка в задачах сжатия. — Информационно-управляющие системы, 2011.

