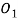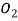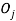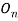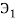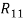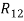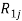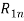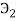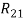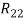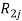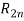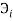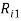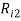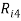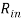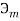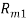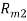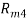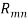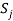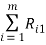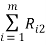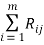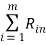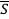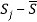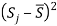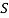В статье рассматриваются теоретические и практические аспекты применения метода экспертных оценок применительно к задаче анализа информационных рисков предприятия. Обсуждаются актуальные вопросы и некоторые возможные проблемы отбора экспертов. Показан пример применения коэффициента конкордации Кендалла для выявления степени согласованности мнений экспертного комитета.

Ключевые слова: информационная безопасность, информационные риски, оценка рисков, экспертные оценки, коэффициент конкордации Кендалла.

Введение

В современных реалиях сложно построить адекватную систему оценки рисков и защиты информации на предприятии. Особенно, если учесть тот факт, что всегда приходится работать в условиях недостаточности и нечеткости информации по угрозам извне и уязвимостям внутри предприятия. Добавим еще к этому факт недостаточности понимания мероприятий по защите информации со стороны руководящего состава организации, которых необходимо убедить в целесообразности принимаемых мер.

Для решения проблемы отсутствия готовых данных и сложности поиска оптимального значения рисков информационной безопасности, а также для принятия объективных, комплексных и компетентных практических решений применяются методы математической обработки экспертных оценок.

Проблема оценки информационных рисков

Как показали многочисленные опыты, человек более правильно (и с меньшими затруднениями) отвечает на вопросы качественного, например, сравнительного, характера, чем количественного. До недавнего времени при рассмотрении качественных явлений использовались исключительно термины «оценивать» или «оценка». То есть происходил процесс оценки, а не измерения. Однако с середины прошлого века в связи с нарастающим проникновением математических, статистических количественных, методов во многие сферы деятельности, термин «измерение» приобрел более широкий смысл, включив в себя также количественные характеристики качественных явлений [1].

Однако несмотря на прогресс и достижения математической науки, в области информационной безопасности и оценки рисков четкой методики количественного расчета величин рисков как не было, так и нет. Это связано в первую очередь с отсутствием достаточного объема статистических данных о вероятности реализации той или иной угрозы. В результате наибольшее распространение получила качественная оценка информационных рисков. Но как использовать результаты такой оценки? Как рассчитывать возможный ущерб и размер необходимых инвестиций для предотвращения реализации рисков?

В настоящее время идет активное накопление данных, на основании которых можно было бы с приемлемой точностью определить вероятность реализации той или иной угрозы, а, следовательно, получить количественную оценку риска, однако накопившихся данных недостаточно и новые угрозы появляются гораздо быстрее, чем хотелось бы [2].

В таких условиях наиболее эффективным методом работы является экспертный метод. Который на сегодняшний день разработан и успешно применяется в России и за рубежом как средство повышения надежности решения научных, управленческих, политических проблем. Эффективность и его широкая применимость объясняется тем, что при решении сложных задач один специалист не в состоянии учесть все факторы и взаимосвязи между ними или оценить вероятности большого числа альтернатив. Очевидно, что гораздо лучшие результаты покажут групповые экспертизы. Основная идея которых — это то, что мнение группы специалистов всегда будет шире мнения одного отдельного взятого, а их взаимодействие позволит скомпенсировать смещение оценок отдельных членов группы и сумма информации, имеющейся в распоряжении группы экспертов, будет больше, чем информация любого члена группы.

Отбор экспертной группы

Этап отбора экспертов является одним из самых важных аспектов оценки рисков, поскольку напрямую коррелирует с получаемыми в итоге результатами.

Разработать методы отбора экспертов, гарантирующих полную достоверность получаемой от них информации, практически невозможно. На практике задача заключается в обеспечении процедуры отбора экспертов, минимизирующей искажения информации, возникающие вследствие некомпетентности отобранных специалистов или их нежелания давать достоверную и надежную информацию.

На практике методы отбора экспертов можно разделить на объективные и субъективные. Объективный подход имеет, в свою очередь, два варианта –документальный и экспериментальный.

Документальный метод предусматривает подбор экспертов на основе анкетных и социально-демографических данных.

Экспериментальный метод проводится на основе испытания, тестирования кандидата в эксперты, либо по результатам эффективности его прежней экспертной деятельности.

При субъективном подходе отбора экспертов первым делом проводится аттестация — ранжирование экспертов с помощью открытого или тайного голосования потенциальных членов будущей экспертной группы с отводом тех из них, кто не набрал определенного минимума голосов. На практике часто применяется способ, когда каждый эксперт оценивает компетентность всех членов экспертной группы, в том числе и свою собственную, используя заранее установленную балльную шкалу [3].

Важно отметить, что ни один из перечисленных методов и приемов отбора экспертов не является универсальным и для точного результата в дальнейшем крайне желательно, чтобы методика отбора должна базировалась на сочетании различных приемов.

В конечном итоге должна получиться экспертная группа численностью 10–15 человек. Увеличение членов экспертной группы экспертов не дает существенного прироста новой информации ни в деталях, ни, главное, по качеству.

Математическая обработка экспертных оценок

Пусть некоторая группа из m экспертов провела ранжирование по значимости данных по характеристикам. Обозначив через ранг, присвоенный экспертом объекту, получим последовательностей рангов. Далее вычислим сумму рангов , присвоенных каждой характеристике всеми экспертами, т. е. суммы элементов столбцов матрицы )

(

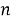
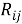
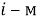
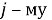
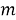
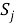
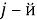
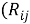
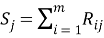
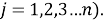
Следующим этапом найдем среднее значение суммы рангов одного объекта S. Сумма всех рангов матрицы равна произведению числа строк матрицы на сумму рангов каждой строки , то есть . Разделив сумму всех рангов на числе характеристик , получим среднее значение суммы рангов одной характеристики:

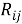
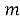
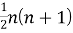
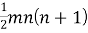
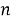
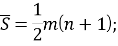
Определив разности ( рангов, присвоенных каждой характеристике всеми экспертами, и средним значением суммы рангов найдем сумму квадратов отклонений:

;

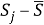
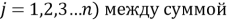
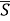
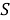
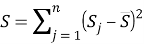
Результаты выполненных действий занесем в Таблицу 1.

Таблица 1

Таблица рангов и расчет коэффициента конкордации

В случае, если бы все мнения экспертов совпали, было бы следующее равенство:

(

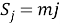
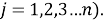
Если учесть, что указанные суммы необязательно располагаются в порядке возрастания, сумма квадратов отклонений будет принимать максимальное значение, если:

= = = = ;

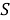
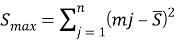
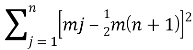
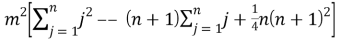
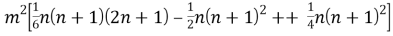
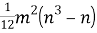
Итак, получается, что

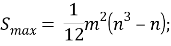
Однако на практике зачастую во мнениях экспертов возникают некоторые расхождения, когда , поэтому целесообразно коэффициент конкордации (согласованности) W определять следующим образом:

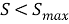
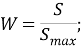
И таким образом итоговая формула коэффициента конкордации получается такой:

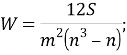
При величине данного коэффициента менее мнения экспертов считаются несогласованными. При нахождении величины коэффициента в диапазоне от согласованность считается средней. При величине более согласованность принимается как высокая.

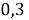
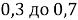
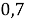
Для того чтобы определить, присутствует ли согласованность в оценках экспертов, выдвинем статистические гипотезы. Нулевая гипотеза предполагает полную рассогласованность мнений экспертов и статистическую недостоверность рассчитанного коэффициента конкордации, конкурирующая гипотеза предполагает, что во мнениях экспертов присутствует согласованность, и рассчитанный нами коэффициент конкордации статистически достоверен. Используем критерий

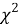
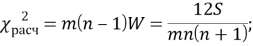
Расчетное значение сравниваем с табличным, соответствующим принятому уровню значимости числу степеней свободы . Если то коэффициент конкордации W значим на выбранном уровне значимости — мнения экспертов согласованы между собой. В противном случае принимать результаты экспертного комитета нельзя, поскольку они рассогласованные.

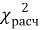
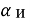
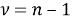
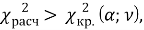
Заключение

Был рассмотрен, проанализирован и показан метод расчета согласованности мнений при работе с экспертными оценками. В условиях недостаточной и нечеткой информации, коей является сфера оценки рисков безопасности предприятия, применение экспертного метода является единственной возможностью получить доказанные количественные оценки по какому-либо анализируемому аспекту.

Литература:

1. Орлов, А. И. Организационно-экономическое моделирование: в 3 ч. / А. И. Орлов. — М.: МГТУ им Н. Э. Баумана, 2011. — ч.2: Экспертные оценки — 567 с.
2. Козлова Е.А Оценка рисков информационной безопасности с помощью метода нечеткой кластеризации и вычисления взаимной информации // Молодой ученый. — 2013 — № 5 (52). — С. 154–161. — URL: https://moluch.ru/archive/52/6967/
3. А. А. Дульзон. Разработка управленческих решений: учебник — Томск: Изд-во Томского политехнического университета. — 295 с. 2009