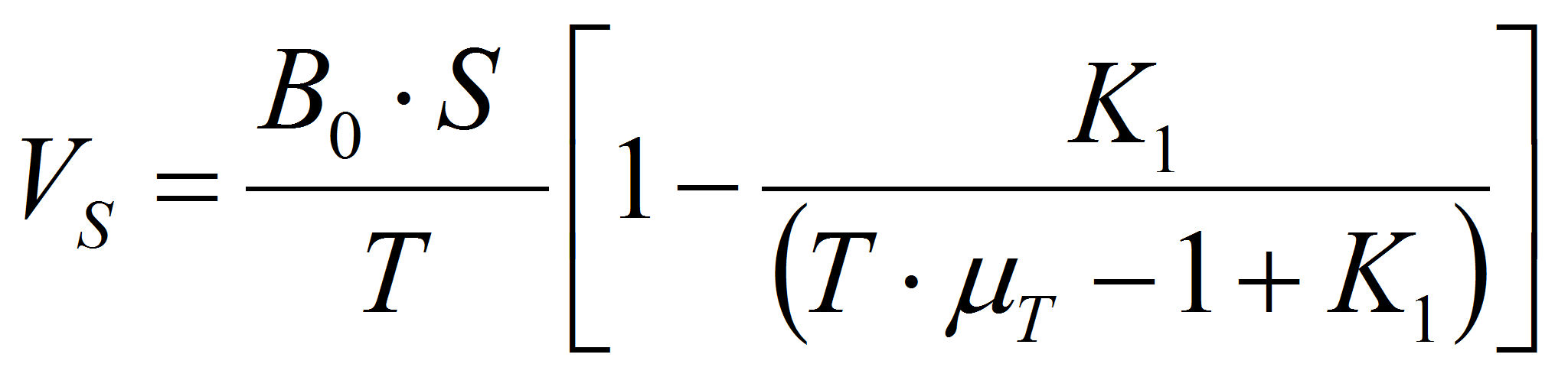Анаэробное сбраживание является медленной микробиологической реакцией. Перемешивание в ходе протекания процесса играет важную роль, т.к.:

- повышает контакт между микроорганизмами и субстратом, что обеспечивает равномерное распределение популяции бактерий;

- обеспечивает равномерное распределение рН и температуры;

- предотвращает отложение плотных твердых веществ на дне и флотацию легких твердых веществ на свободной поверхности;

- позволяет предотвратить формирование пустот и скоплений, уменьшающих рабочую площадь реактора;

- помогает освободить пузырьки биогаза.

В реакторах метанового брожения по интенсивности образования биогаза наиболее предпочтительна система гидравлического перемешивания.

В большинстве биогазовых установок (БГУ) применяется система механического перемешивания, что обусловлено ее дешевизной, однако указанное преимущество справедливо лишь для установок с малым объемом реактора. Еще одним сдерживающим фактором в развитии данного направления является отсутствие комплексных исследований, направленных на совершенствование конструкции и обоснование параметров и режимов работы биореактора с системой гидравлического перемешивания.

Целью данной работы является интенсификация процесса анаэробного сбраживания путем совершенствования системы гидравлического перемешивания.

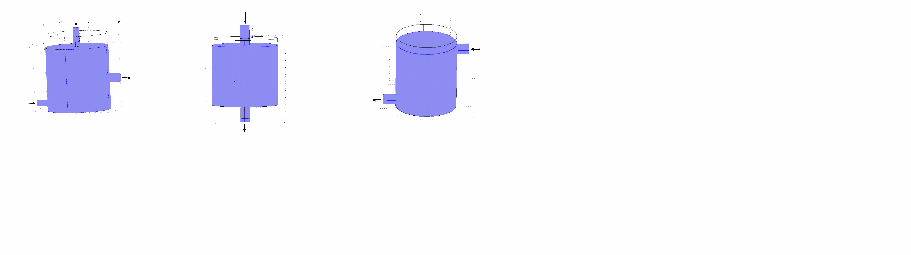
В работе рассмотрено три типа загрузки сырья в системе гидравлического перемешивания (рис. 1):

- модифицированный тип загрузки 1, перемешивание в реакторе осуществляется рециркуляцией субстрата через два подводящих патрубка, при этом в верхнем подводящем патрубке находится аксиально-лопаточный закручиватель;

- тип загрузки 2, при котором подача субстрата осуществляется через подводящий патрубок, расположенный в верхней крышке корпуса реактора, а отгрузка шлама через отводящий патрубок на дне реактора [1];

- тип загрузки 3, при котором подводящий и отводящий патрубки расположены на противоположных боковых сторонах корпуса реактора [2].

способ загрузки 1 способ загрузки 2 способ загрузки 3

Рис.1 Расположение входных и выходных труб.

При построении математической модели приняты следующие допущения: рассматриваемая среда (органический субстрат) предполагается гомогенной жидкостью [3-7] с плотностью и коэффициентом эффективной вязкости, зависящими от концентрации дисперсной фазы; процесс перемешивания нестационарный. С помощью ротационного вискозиметра RM 100, было установлено, что органический субстрат с концентрацией сухого вещества до 5%, используемой при гидравлическом перемешивании, обладает ньютоновскими свойствами.

Математическая модель, описывающая процессы переноса массы, импульса и энергии при циркуляции органического субстрата в резервуаре биореактора определяется гидродинамическим режимом. Процессы анаэробного брожения органического сырья, происходящие в результате жизнедеятельности бактерий, предполагают низкие скорости движения жидкости в резервуаре [8]. Согласно [9] струя остается ламинарной при числе Re<30, рассчитанном для скорости истечения из отверстия. Принимая во внимание геометрические характеристики реактора, диапазон изменения вязкости для различных концентраций субстрата [10], гидродинамический режим циркуляции субстрата в биоректоре можно считать ламинарным.

Математическая модель в тензорном виде

где - вектор ускорения свободного падения; - плотность органического субстрата; -объемная доля (концентрация) дисперсной среды; t – время; - вектор скорости; Т – температура; - коэффициент теплопроводности; С_р – коэффициент удельной теплоемкости; Т - тензор напряжений , где D - тензор скоростей деформаций, ; р - давление; I - единичный тензор; - эффективная вязкость.

Начальное распределение объемной концентрации при t=0 задается для условия осаждения осадка на дно резервуара.

Начальные гидродинамические условия .

Граничные условия для скорости: на твердых границах резервуара задаются условия прилипания жидкости ; на входных отверстиях задаются профили скорости, соответствующие сформировавшемуся профилю скорости ньютоновской жидкости в круглой трубе; полагая, что выход из резервуара представляет трубу такой длины, на выходе из которой можно считать движение жидкости установившимся, принимаем в качестве граничных условий на выходе условие стабилизации скорости. На открытой границе , где - давление газа, - нормаль к поверхности субстрата, - тензор скоростей деформаций.

Решение поставленной задачи невозможно получить в явном виде, поэтому использовался пакет моделирования COMSOL, позволяющий решать системы нелинейных дифференциальных уравнений в частных производных методом конечных элементов. На основе возможностей программы COMSOL была создана новая пользовательская модель, адаптированная к условиям рассматриваемой задачи.

Достоверность полученных результатов была проверена путем сравнения аналитического решения задачи истечения круглой струи из отверстия и решения, полученного с применением программного пакета COMSOL.

COMSOL Multiphysics предназначен для моделирования и расчетов задач, основанных на дифференциальных уравнениях в частных производных. В основу программного пакета COMSOL Multiphysics заложен численный метод решения задач прикладной физики - метод конечных элементов. Программное обеспечение пакета позволяет осуществлять адаптивное построение сетки и контроль ошибок при работе с различными численными решателями.

Аналитическое решение задачи истечения ламинарной круглой струи из отверстия было получено Шлихтингом [9]. После истечения струя смешивается с покоящейся окружающей жидкостью. Распределение скоростей имеет вид:

,

где , - координаты цилиндрической системы координат; , - продольная и радиальная составляющие вектора скорости; - кинематическая вязкость, - кинематический импульс.

В COMSOL задача моделировалась в двумерной геометрии с аксиальной симметрией. Рабочая область представлялась в виде цилиндра (, ) с отверстием радиуса с координатами (0,0). При этом 0,0002, а 0,0001. Для описания гидродинамических процессов использовалось уравнение Навье-Стокса.

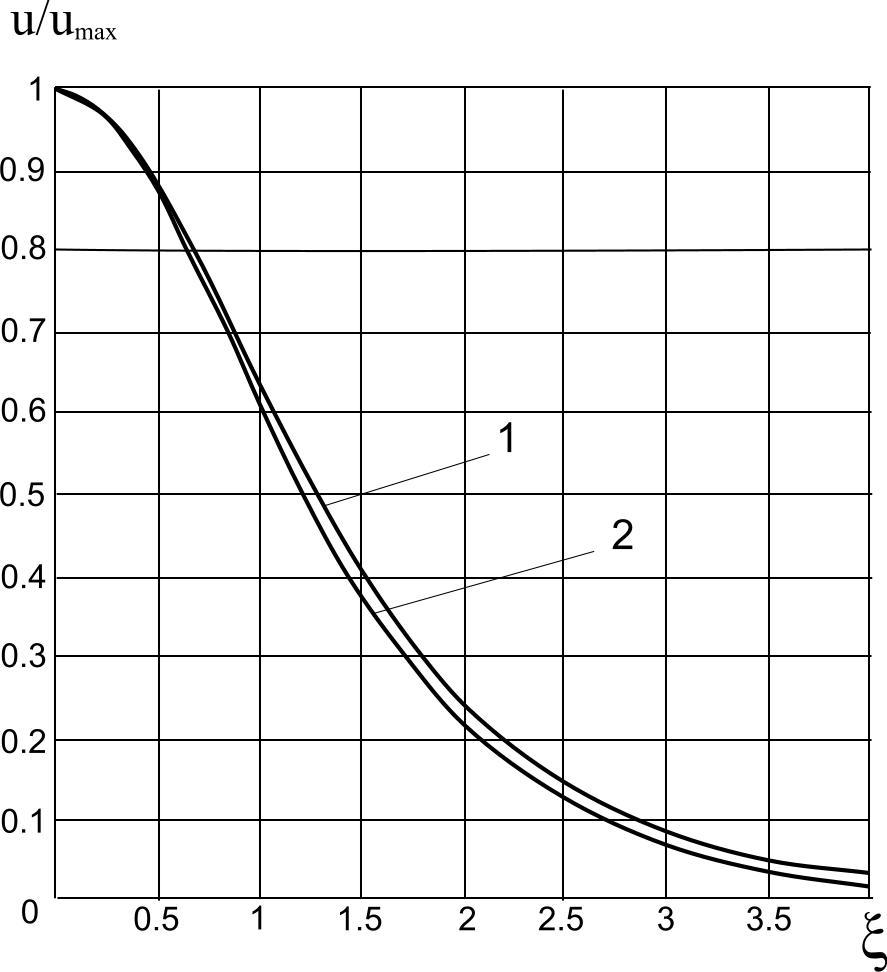
На рисунке 2 представлены кривые, представляющие распределение продольной составляющей вектора скорости, полученные аналитическим методом решения (кривая 1) и численным (кривая 2). Как видно из рисунка, наблюдается достаточно хорошее согласование между кривыми, что позволяет судить о достаточной достоверности и правильности результатов решений такого типа задач, получаемых с помощью программного пакета COMSOL.

Рис.2 Распределение продольной составляющей вектора скорости.

Расчеты для 1 типа загрузки проводились с учетом того, что на входе в резервуар верхней загрузочной трубы установлен аксиально-лопаточный закручиватель. При этом закон изменения скорости на входе был задан в виде и , где - радиус входной трубы; - угол закрутки потока [11].

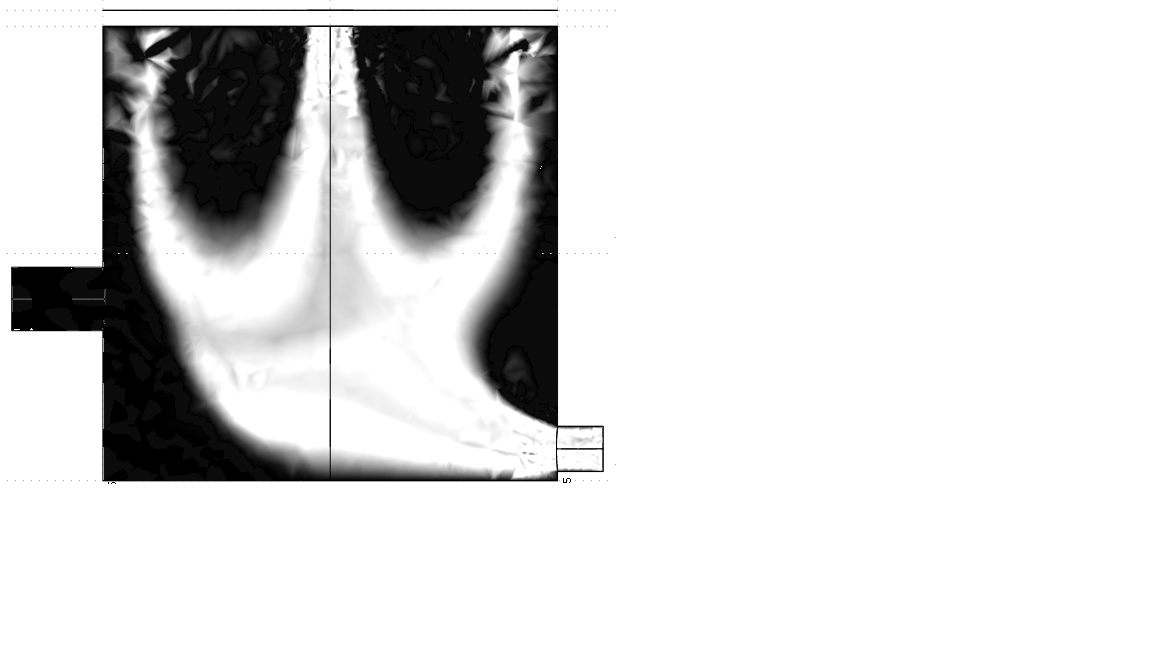
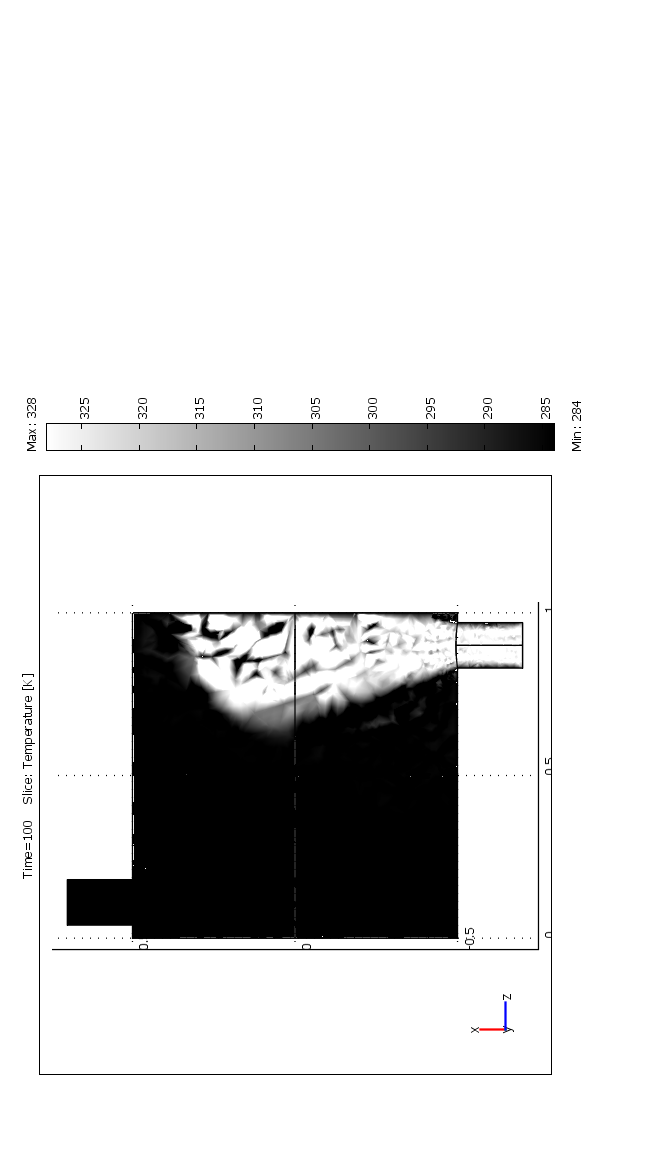
На рисунке 3 представлено распределение температуры внутри реактора при разных типах загрузки.

способ загрузки 1 способ загрузки 2 способ загрузки 3

Рис.3. Распределение температуры внутри реактора на плоскости y=0, Re=21,5, t=1000 при разных типах загрузки.

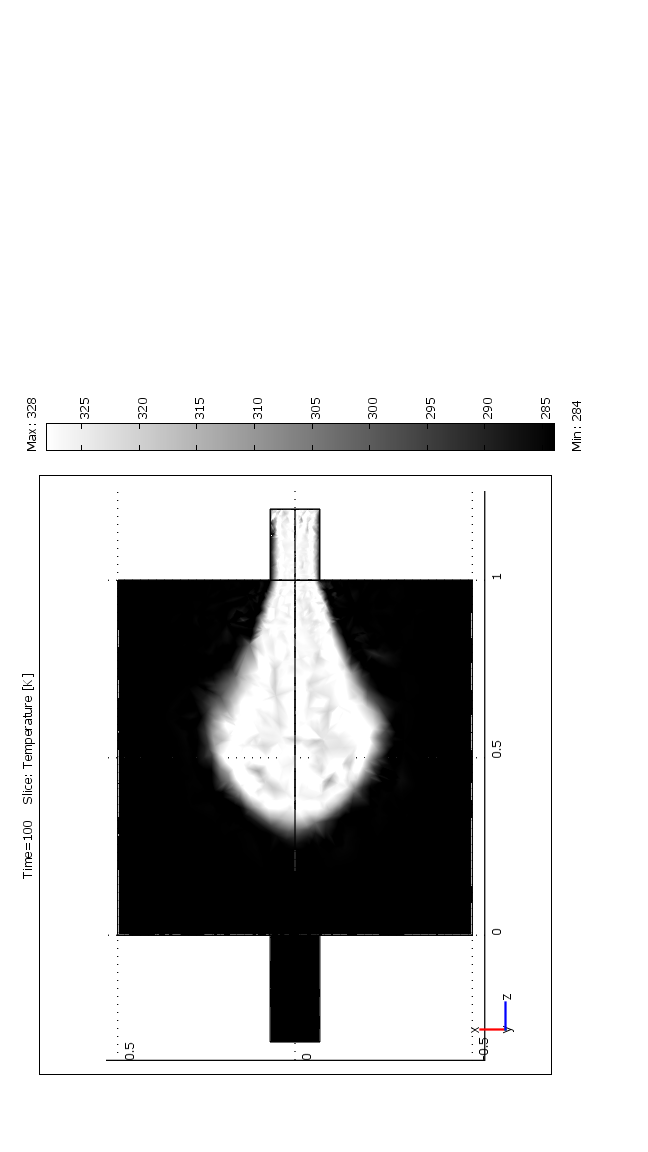
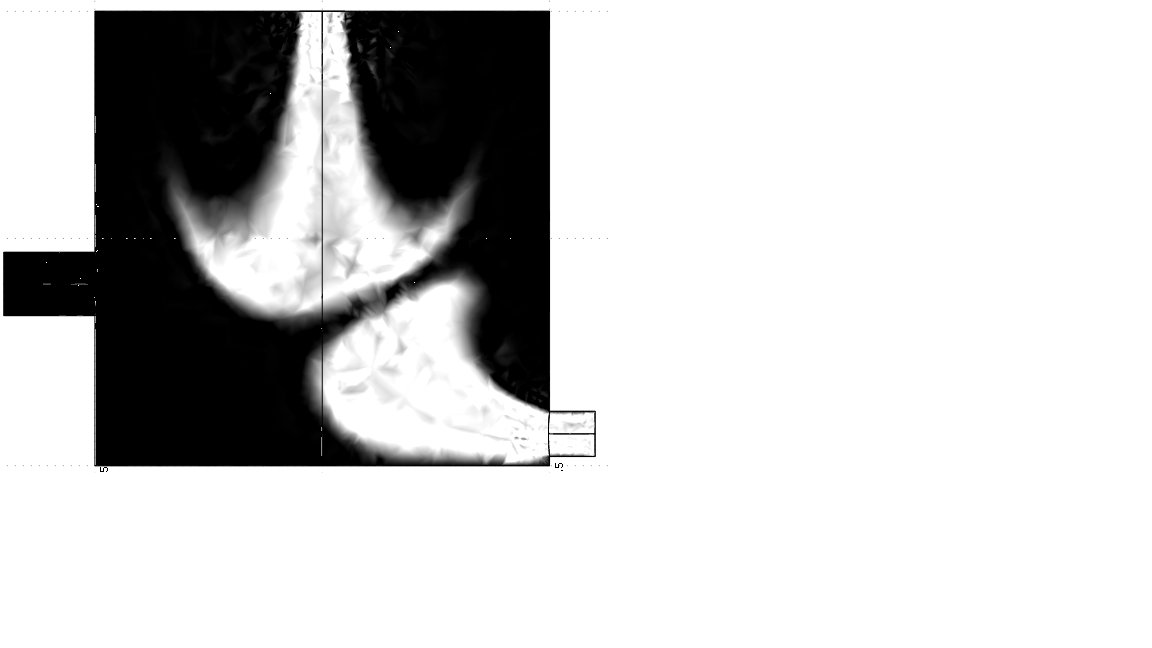
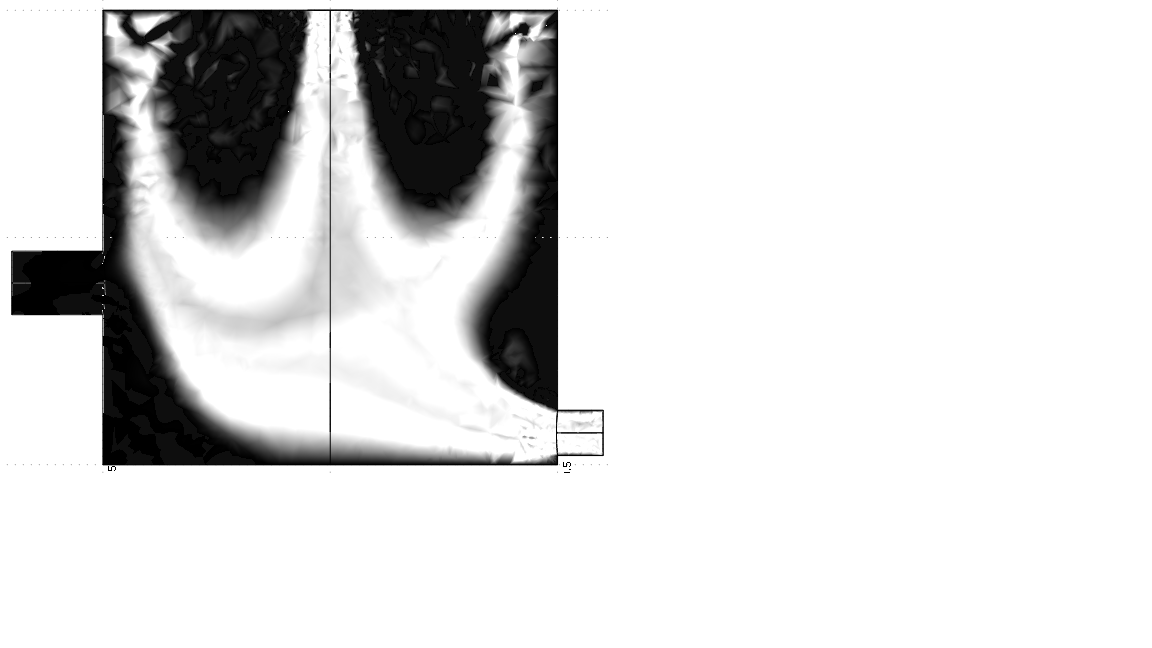
Распределение температурных полей по времени в реакторе с модифицированным способом загрузки представлено на рисунке 4.

у=0: t=500 t=1000 t=3000

Рис. 4. Распределение температуры внутри реактора на плоскости у=0 при Re=10,7 для разных значений времени t для модифицированного способа загрузки.

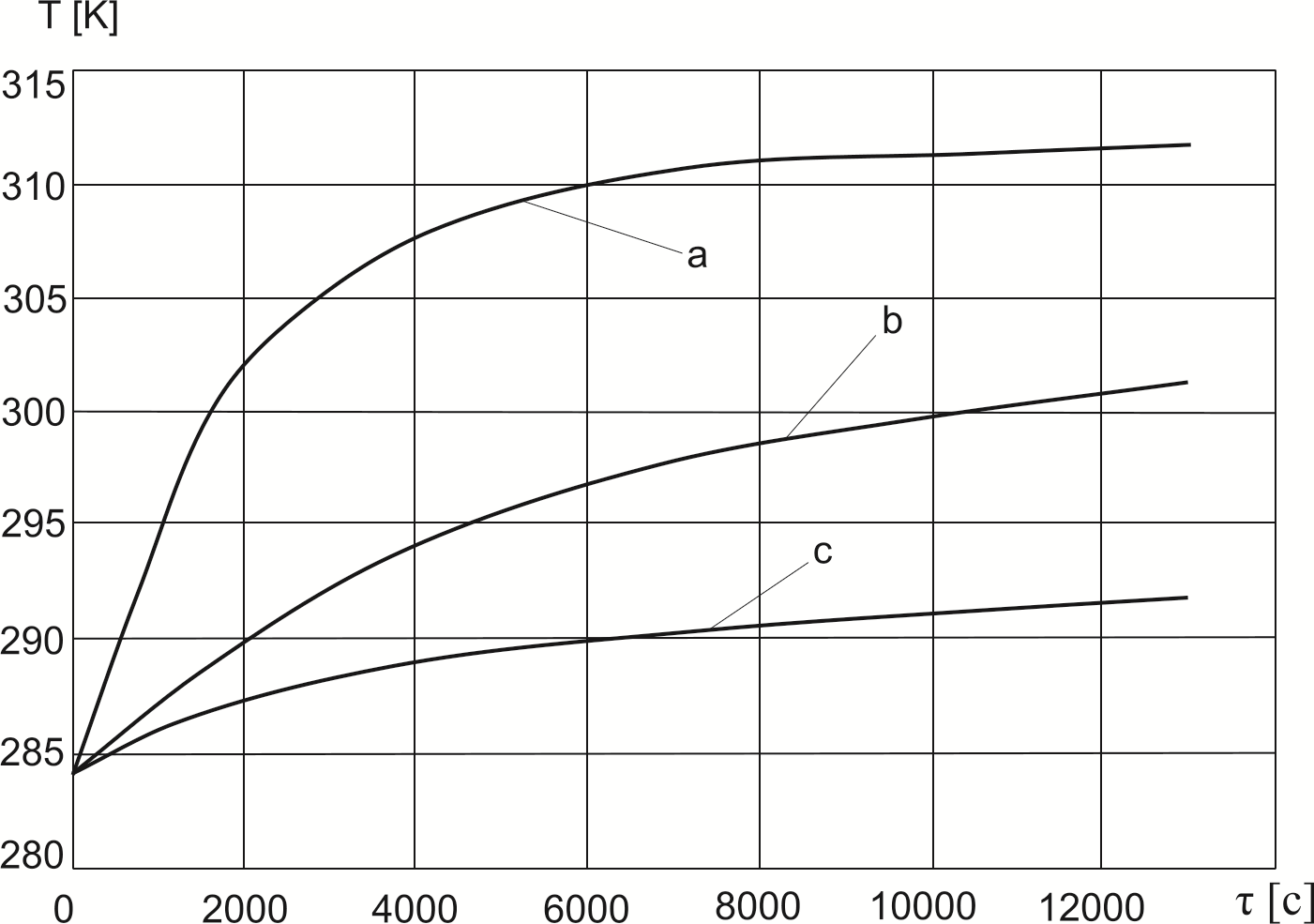
Получены зависимости изменения средней температуры органического субстрата в реакторе БГУ при различный способах загрузки по времени (рис. 5).

Рис.5 Изменение средней температуры субстрата в реакторе по времени.

a –модифицированный тип загрузки; b –тип загрузки 2; c –тип загрузки 3.

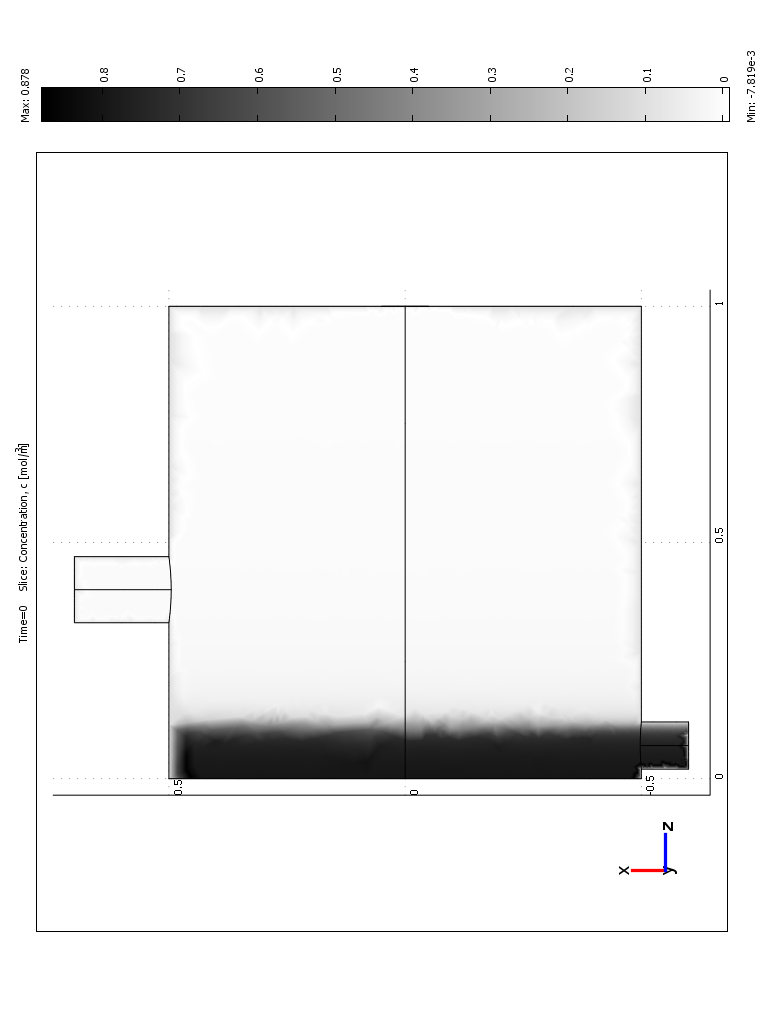
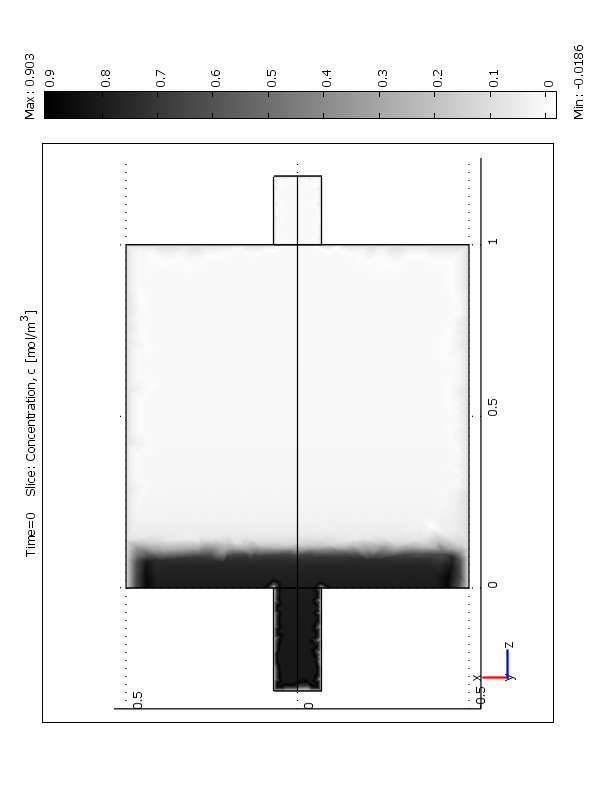
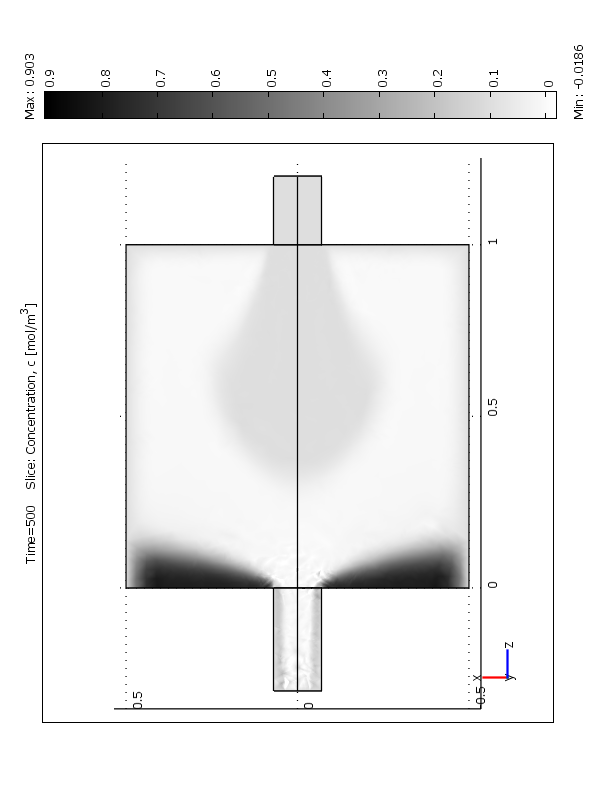
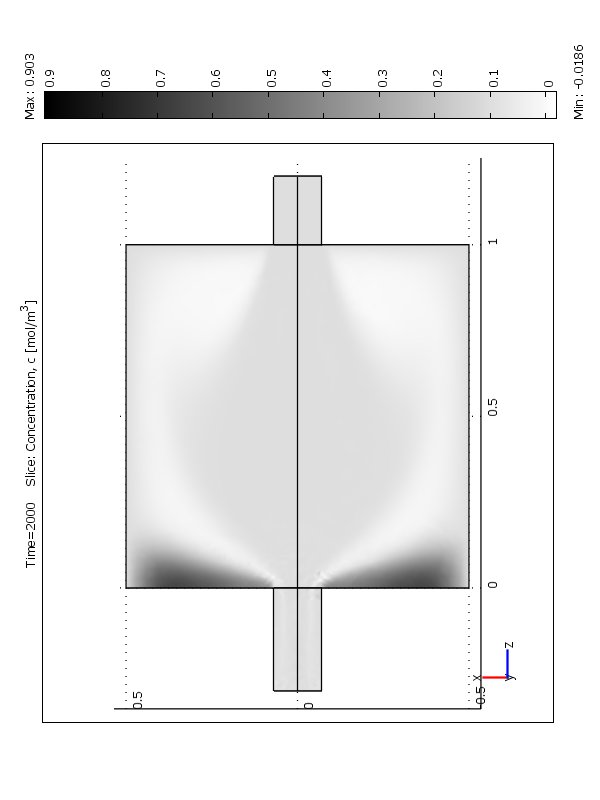
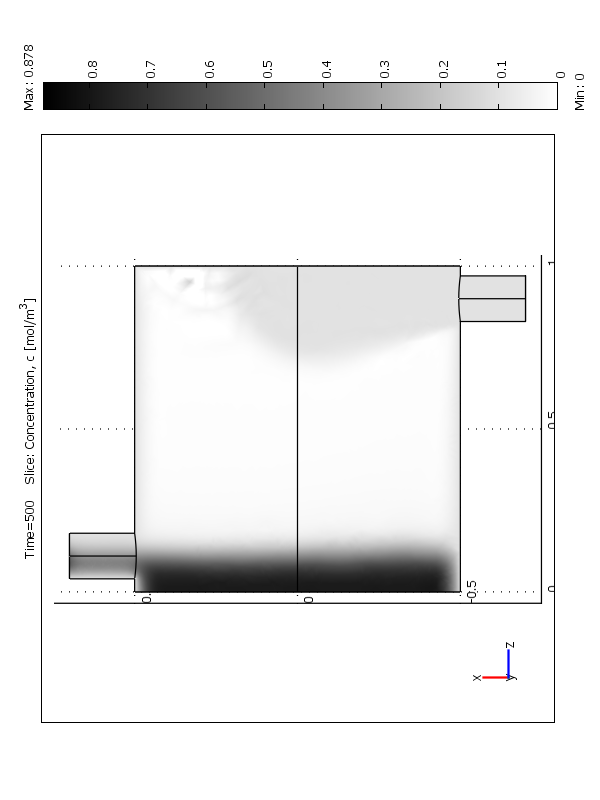
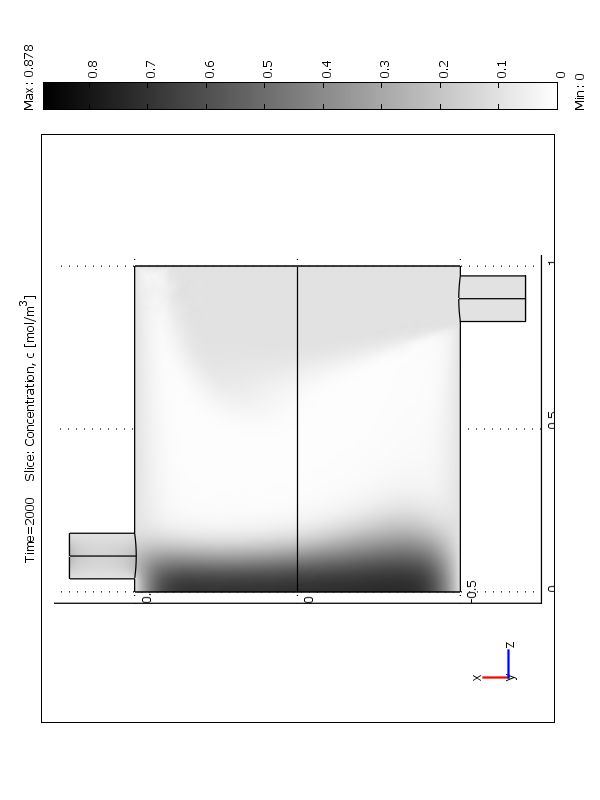
На рисунке 6 представлено изменение распределения концентрации твердой фазы по времени. Как видно из рисунка с течением времени распределение дисперсной фазы становится более однородным.

t=0 t=500 t=2000

a:

b:

c:

Рис.6 Распределение полей концентрации (объемные доли) по времени:

а- 0 сек; b – 1000 сек; c – 3000 сек.

a –модифицированный тип загрузки 1; b –тип загрузки 2; c –тип загрузки 3.

Проводился сравнительный анализ качества перемешивания в БГУ с представленными типами загрузки. Сравнение проводилось для расхода Q=0.0003 м³/с c одинаковой площадью поперечного сечения входных труб.

В качестве критерия перемешивания по объему использовалось отношение

,

[10].

где В₀ - предельный выход биогаза из единицы органического субстрата; S – концентрация органического субстрата; К - кинематический коэффициент, ; - максимальная скорость роста микроорганизмов, ; Т – время; равно значению при , где - средняя концентрация органического субстрата (рис. 7).

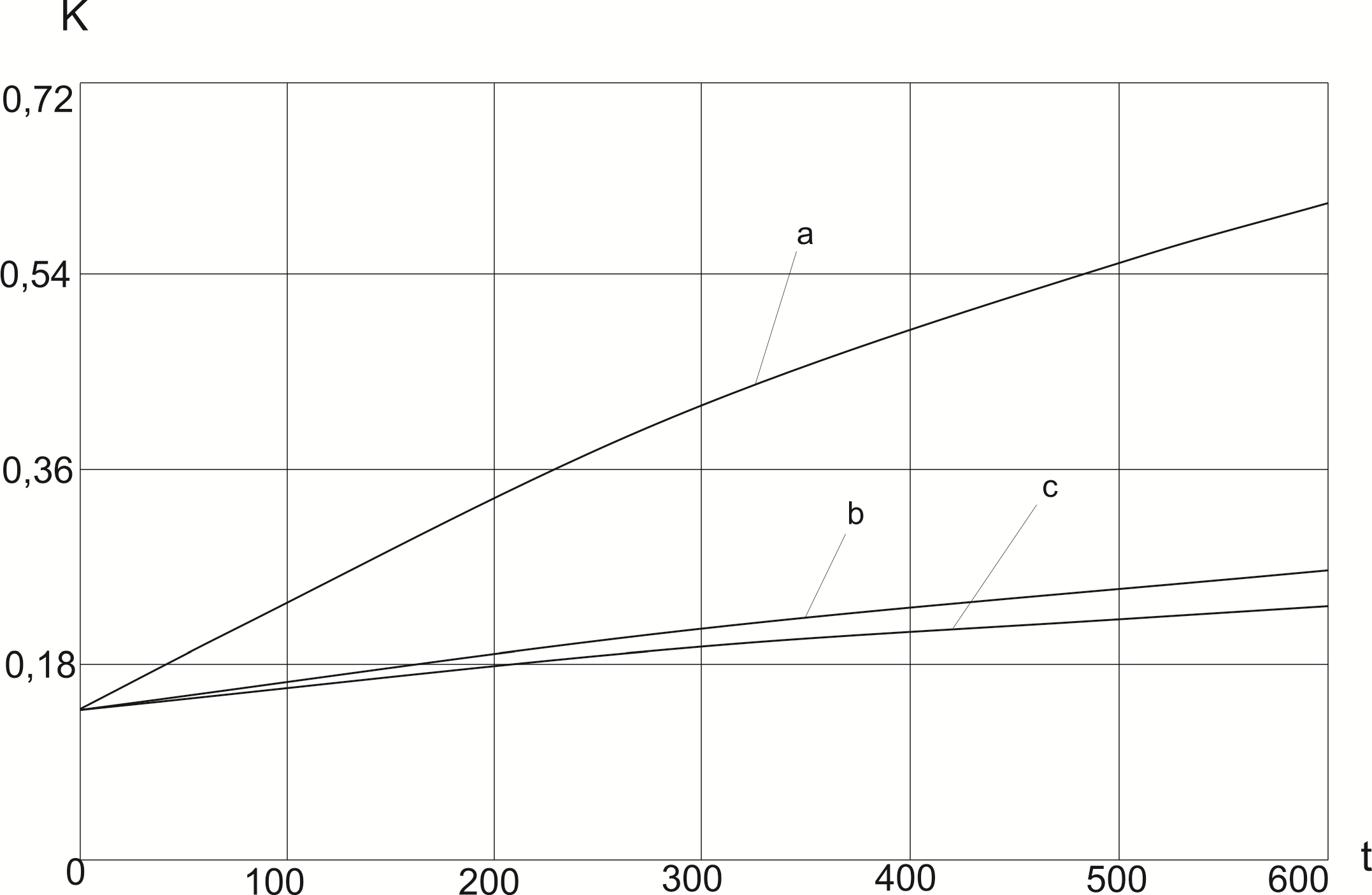
Рис.7. Изменение критерия перемешивания по времени.

a –модифицированный тип загрузки; b –тип загрузки 2; c –тип загрузки 3.

Согласно результатам численных расчетов первый тип загрузки обеспечивает лучшее перемешивание и является наиболее предпочтительным из рассматриваемых вариантов.

Выводы

1. Полученная математическая модель позволяет проводить численные исследования процессов теплопереноса и гидродинамики в реакторе биогазовой установки при гидравлическом перемешивании.
2. Получено распределение температуры и концентрации органического субстрата внутри реактора.
3. Предложен критерий перемешивания, позволяющий оценить качество перемешивания сбраживаемого субстрата в реакторе БГУ.
4. Проведены численные исследования и сравнительный анализ циркуляции органического субстрата и соответствующего им распределения объемной концентрации дисперсной среды в резервуарах с различным расположением входных и выходных труб. В результате доказано, что предлагаемое в работе расположение обеспечивает лучшее перемешивание и предотвращает свободную поверхность смеси от образования корки.

Литература:

1. Веденеев А. Г., Веденеева Т. А. Биогазовые технологии в Кыргызской Республике. Бишкек: Евро, 2006. 90с.
2. Пат. РФ № 94034739/25, 19.09.1994.
3. Moeller, G., Torres, L.G., 1997. Rheological characterization of primary and secondary sludge treated by both aerobic and anaerobic digestion. Bioresour. Technol. 61, 207–211.
4. Murakami, H., Katayama, H., Matsuura, H., 2001. Pipe friction pressure loss in transportation of high-concentration sludge for centralized solids treatment. Water Environ. Res. 73 (5), 558–566.
5. Sanin, F.D., 2002. Effect of solution chemistry on the rheological properties of activated sludge. Water SA 28 (2), 207–211.
6. Brar, S.K., Verma, M., Tyagi, R.D., Valero, J.R., Surampalli, R.Y., 2005. Sludge based Bacillus thuringiensis biopesticides: viscosity impact. Water Res. 39 (13), 3001–3011.
7. Wu, B., Chen, S., 2007. CFD simulation of non-Newtonian fluid flow in anaerobic digesters. Biotechnol. Bioeng. 99, 700–711.
8. Гюнтер Л. И., Гольдфарб Л. Л. Метантенки. М.: Стройиздат, 1991. 128с.
9. Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1974. 713с.
10. Филиппов А.К., Голубев Л.Г. Альтернативное газо-теплоснабжение малых фермерских хозяйств на базе модульного биореактора. Гидродинамика отопительно-вентиляционных устройств: Межвуз.сб.науч.трудов. Казань. 1995. стр.56-61.
11. Назмеев Ю. Г. Гидродинамика и теплообмен закрученных потоков реологически сложных жидкостей. М.: Энергоатомиздат, 1996. 304с.