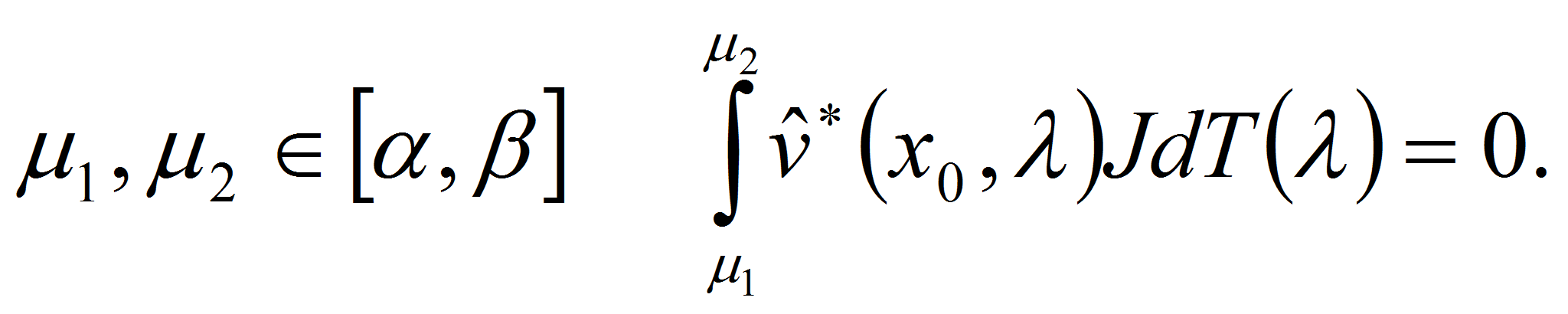Получены оценки ранга спектральной матрицы-функции самосопряженных расширений симметрического дифференциального оператора второго порядка, действующего в пространстве конечномерных вектор-функций, суммируемых с квадратом модуля.

Одной из фундаментальных проблем спектральной теории линейных дифференциальных операторов является исследование их спектральных характеристик в терминах коэффициентов соответствующих дифференциальных операций [1]. Пусть - самосопряженный оператор, действующий в гильбертовом пространстве , порожденный формально самосопряженной дифференциальной операцией второго порядка в пространстве вектор-функций. В этой заметке сопоставляется ранг спектральной матрицы-функции оператора и кратность его спектра.

1. Предположим, что комплексная матричнозначная функция, заданная на всей числовой оси, и - неотрицательная вещественнозначная мера, заданная на борелевской - алгебре подмножеств числовой прямой . Если для любых и - измеримы и интегрируемы по , то будем считать, что и для любого измеримого подмножества .

Предположим, что - мерная, неотрицательно определенная, эрмитова, матричнозначная функция, заданная на ограниченных борелевских подмножествах числовой прямой, причем каждая функция - является счетно-аддитивной на семействе . Матрица задает положительную матричную меру. Каждая функция множества есть неотрицательная вещественнозначная мера и каждая при всех есть комплекснозначная мера. Поскольку для любой неотрицательной эрмитовой матрицы , где - единичная матрица и обозначает след, то каждая функция - абсолютно непрерывна относительно меры . Матричную функцию обычно называют следовой производной от матричной меры . Матричная функция - измерима по Борелю и интегрируема относительно , причем .

Пусть 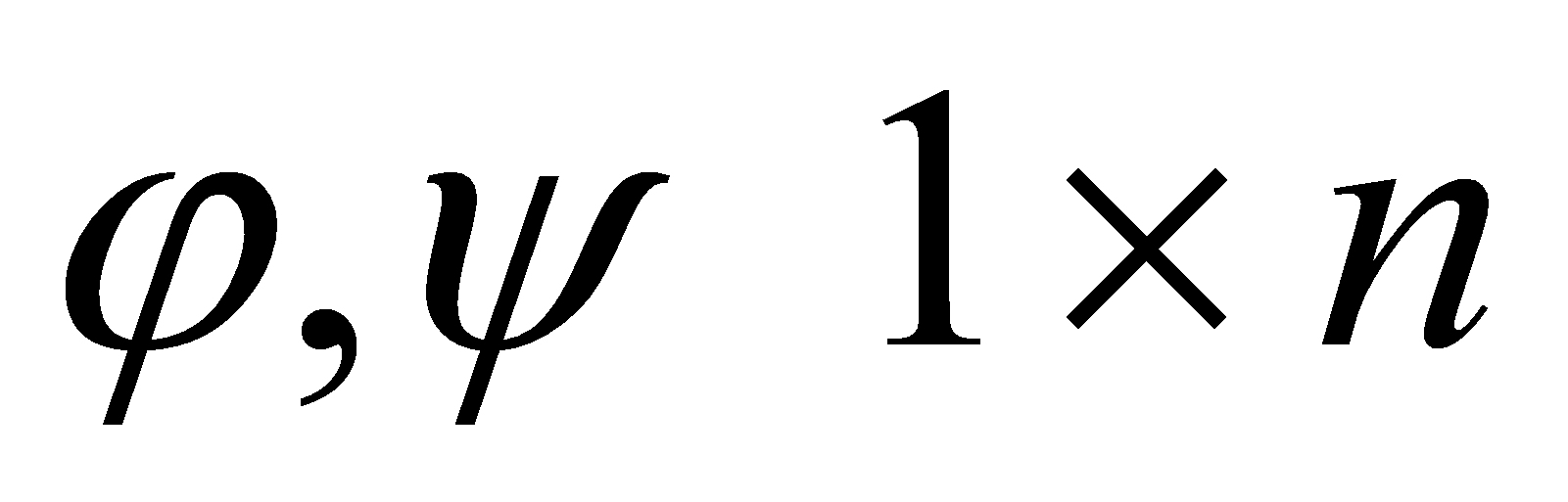- мерные векторнозначные функции на 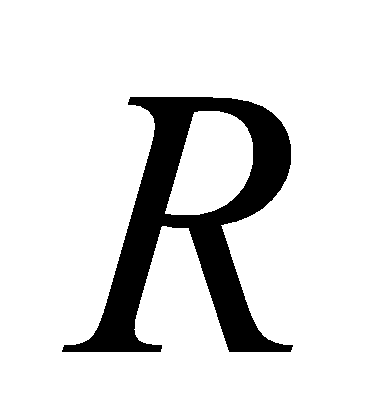. Если 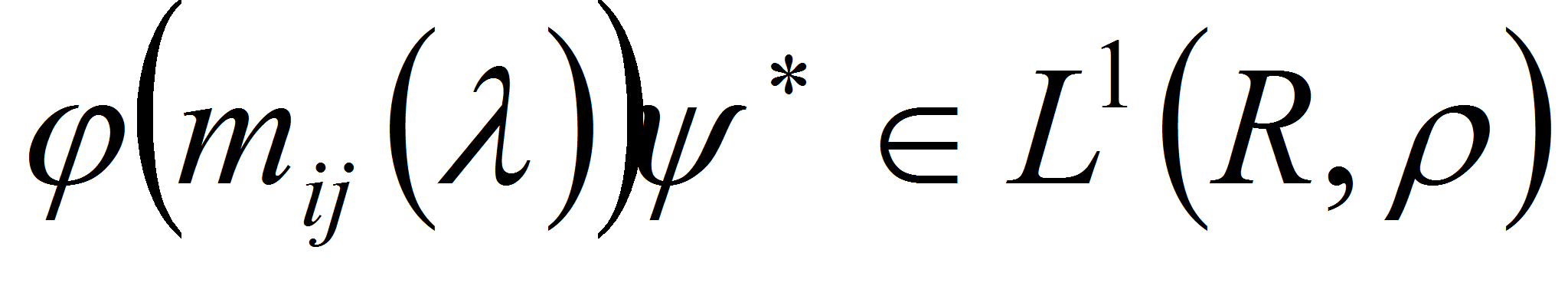, то можно определить скалярное произведение следующим образом

.

Тогда обозначает класс всех измеримых по Борелю вектор-функций , заданных на всей числовой оси таких, что скалярные произведения существуют и конечны. Интеграл иногда записывают в виде . есть гильбертово пространство векторнозначных функций.

Пусть - оператор умножения на независимую переменную в гильбертовом пространстве , где - положительная матричная мера и область определения оператора есть множество .

Введем два гильбертовых пространства , в которых определены линейные операторы . Унитарная эквивалентность между оператором из пространства и из пространства есть сохраняющее норму отображение из пространства в пространство , при котором отображается в некоторое множество таким образом, что для любого имеет место соотношение .

Определение 1. Две положительные матричные меры и не обязательно одинаковой размерности будем называть эквивалентными, если существует унитарная эквивалентность между операторами умножения на независимую переменную в пространстве и в пространстве .

Для - мерной положительной матричной меры введем ее атомическую и непрерывную части, соответственно. Атом есть любое множество, состоящее из отдельной точки , такой что .

Пусть мера 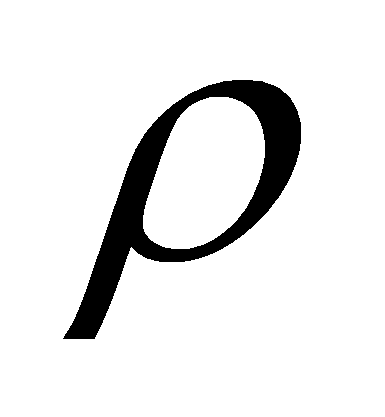эквивалентна мере 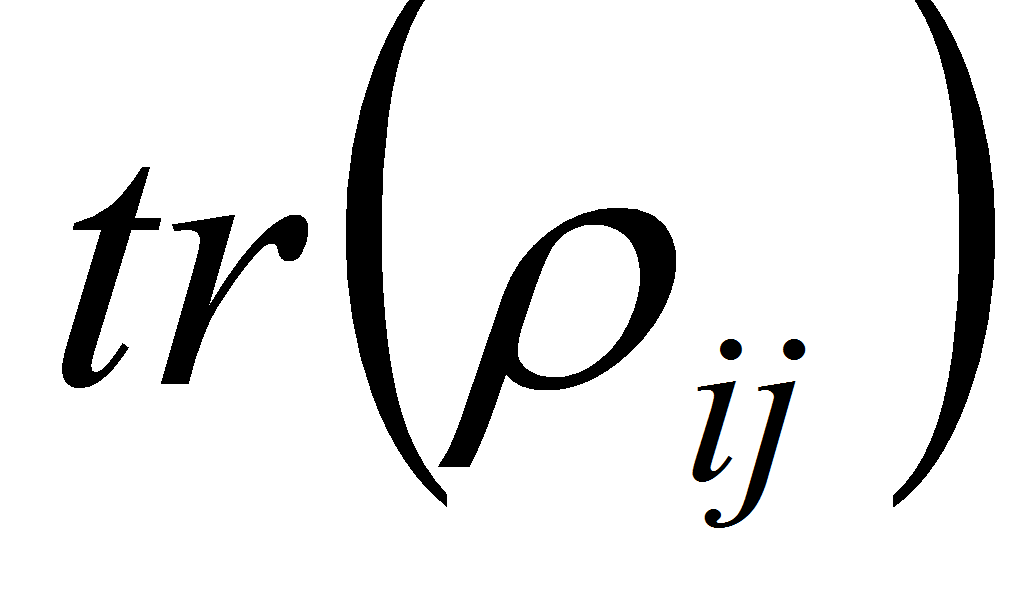и пусть 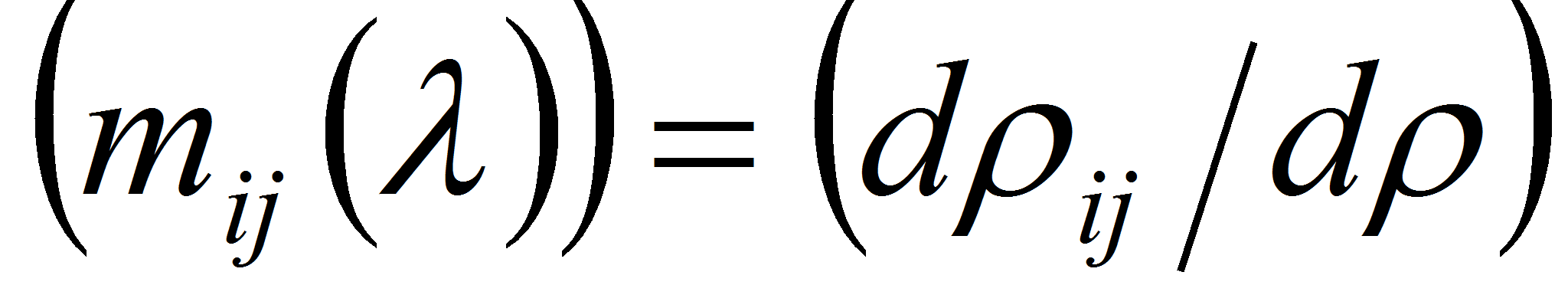, тогда одномерная атомическая мера 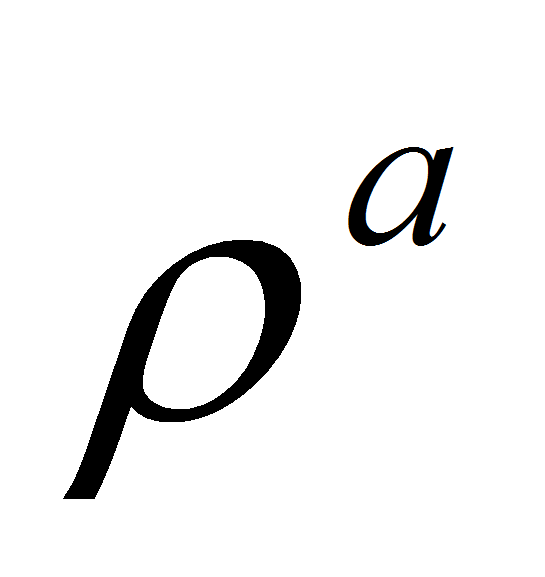эквивалентна мере 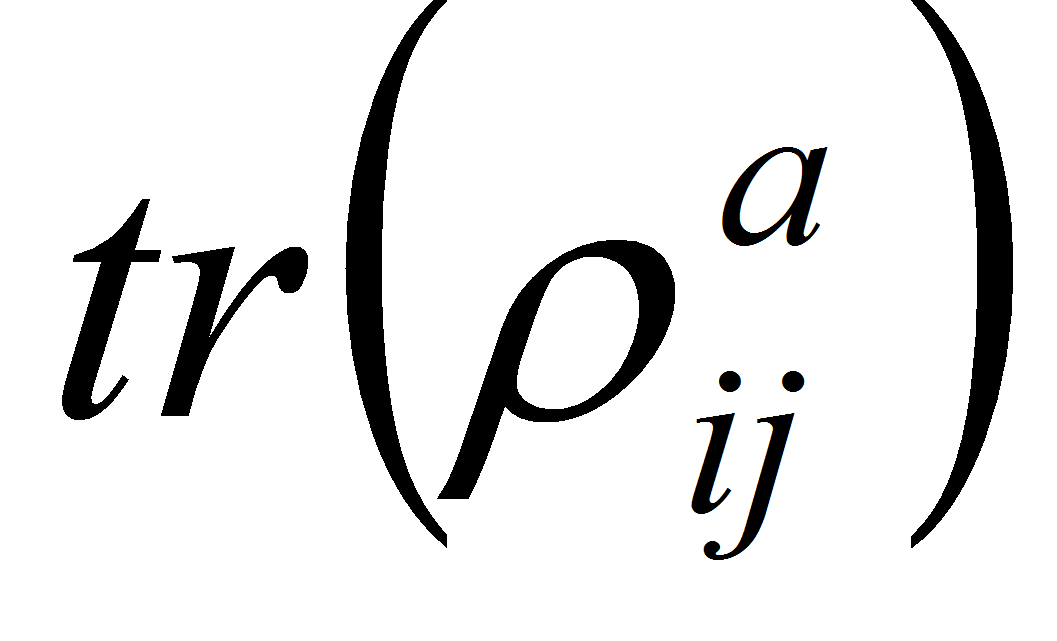и 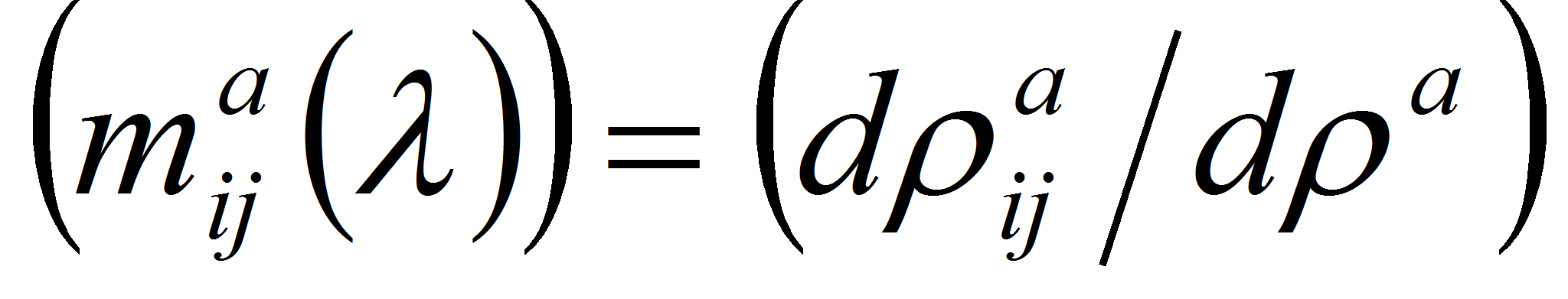, а одномерная непрерывная мера 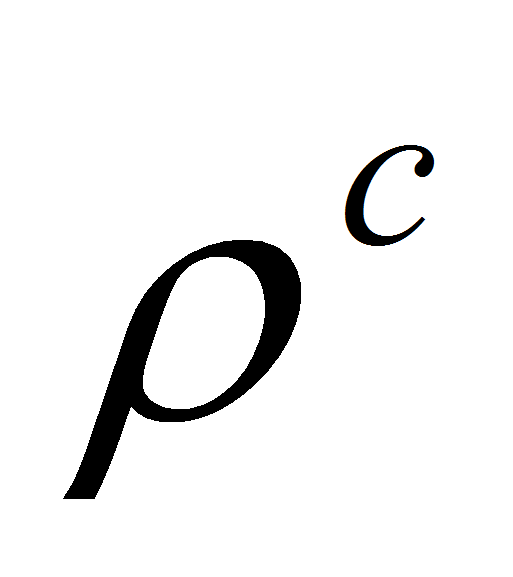эквивалентна мере 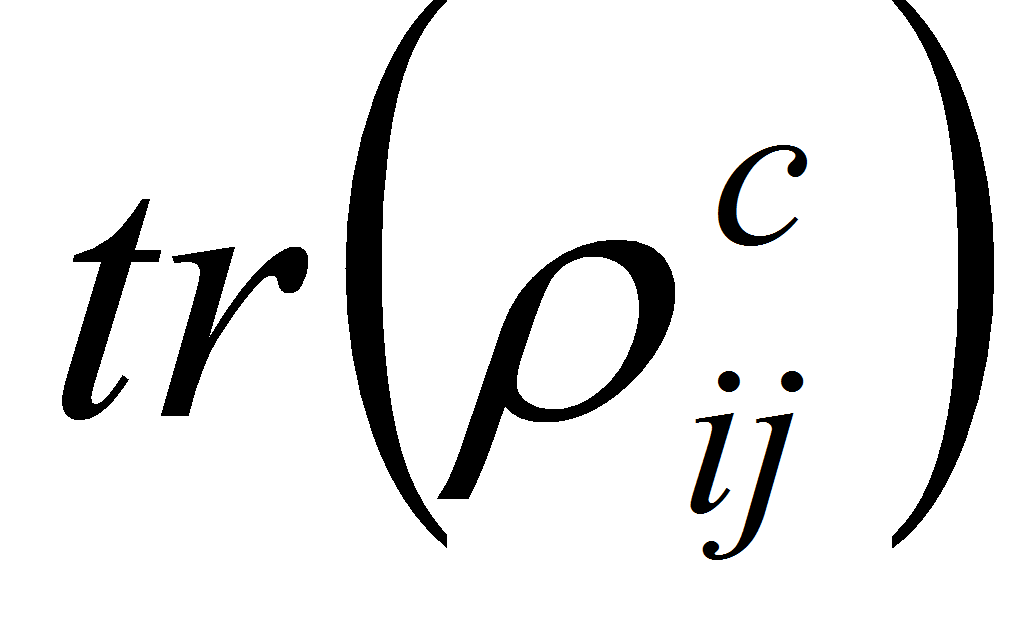и .

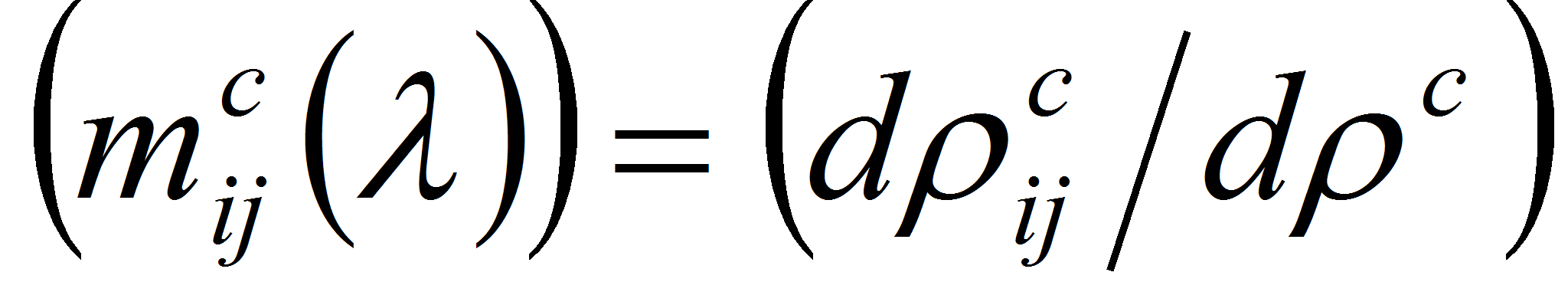Для значений и пусть фиксированная - мерная главная подматрица матрицы . Детерминант есть - измеримая функция от переменной, следовательно, все множества будут - измеримы и, кроме того, имеют место равенства для значений .

Определение 2. Пусть - положительная матричная мера. Ранг в точке обозначим символом и определим соотношением

,

где .

Обозначим через ранг матричной меры на всей числовой оси, т.е. .

Атомический ранг в точке обозначим через . Ранг непрерывной составляющей определим соотношением

.

Лемма 1. .

Определение 3. Спектральная матрица для самосопряженного оператора есть положительная матричная мера , для которой существует унитарная эквивалентность между операторами в пространстве и в пространстве .

Лемма 2. Если спектральная матрица для самосопряженного оператора и есть собственное значение кратности , то . Если не является собственным значением оператора , то .

Теорема 1. Пусть - кратность непрерывного спектра самосопряженного оператора в точке . Если спектральная матрица, соответствующая оператору , и , то .

2. Как известно, каждой спектральной функции минимального оператора отвечает некоторая обобщенная резольвента , определенная формулой

.

При помощи формулы обращения Стилтьеса спектральная функция однозначно восстанавливается по соответствующей ей обобщенной резольвенте ; для любых функций и из и любых вещественных и имеет место равенство:

(1)

Равенство (1) позволяет построить формулу всех спектральных функций оператора по известной обобщенной резольвенте.

3. Пусть выражение имеет вид , где - квадратная матрица-функция порядка . Кроме того, измерима и локально суммируема в сильном смысле и при каждом .

Выражение имеет смысл для каждой вектор-функции , которая на любом отрезке абсолютно непрерывна вместе со своей первой производной и . Скалярный случай рассмотрен в работах автора [2, 3].

Каждой вектор-функции , для которой имеет смысл, поставим в соответствие вектор-функцию . Будем рассматривать при любом как матрицу-столбец. Положим 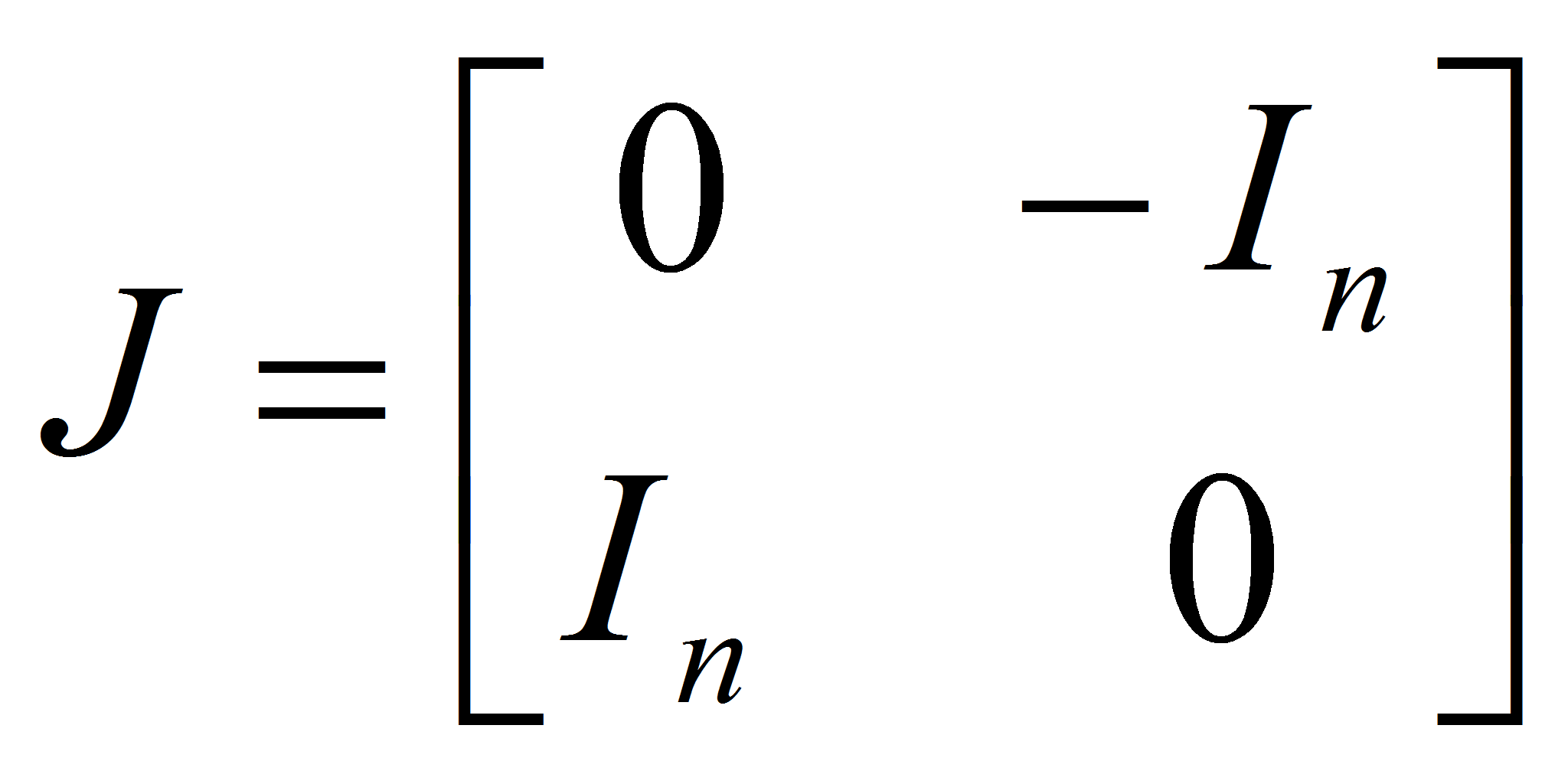, где - единичная матрица порядка . Тогда аналог тождества Лагранжа примет следующий вид .

Через и обозначим фундаментальную систему решений матричного уравнения , удовлетворяющих начальным условиям

где - произвольная фиксированная точка промежутка .

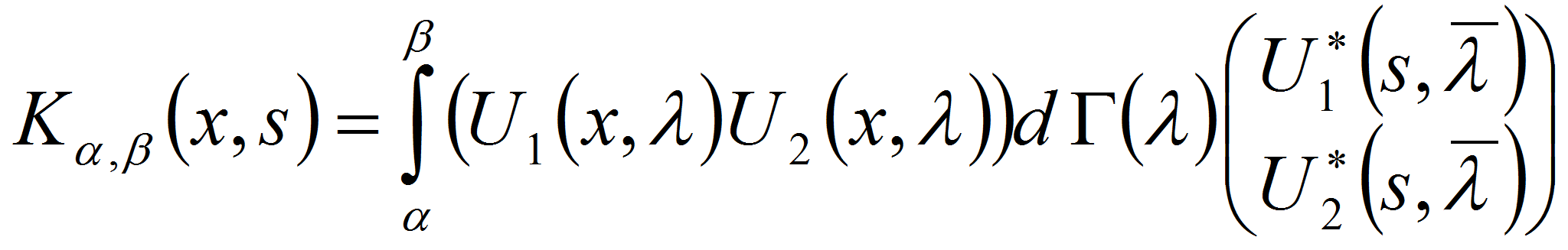Для любых вещественных и оператор является интегральным, а его ядро - представимо в виде , где - эрмитово неубывающая матрица-функция порядка , называемая спектральной функцией распределения оператора .

Лемма 3. Пусть для любого уравнение имеет решение такое, что:

1) , где какая-либо внутренняя точка промежутка ;

2) для любой вектор-функции

3) для фиксированного вектор-функция удовлетворяет условию Липшица относительно на сегменте .

Тогда для любых

Теорема 2. Пусть при любом уравнение имеет линейно независимых решений

(2)

таких, что:

1. для каждого из первых решений (2)

а)

б) какова бы ни была вектор-функция ;

2. для каждого из последних решений (2)

а)

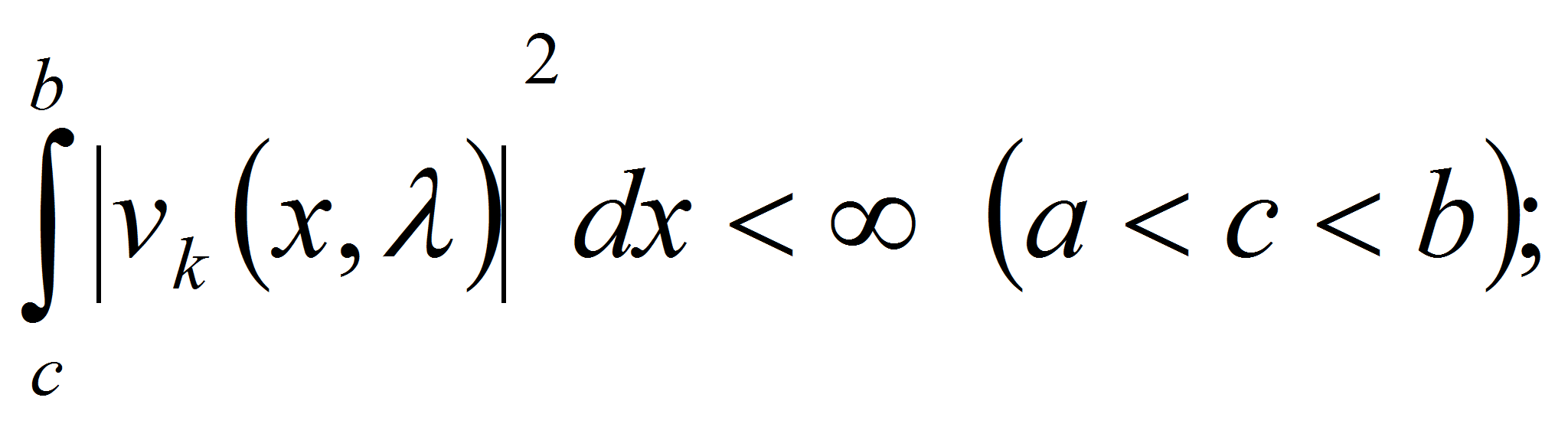
б) 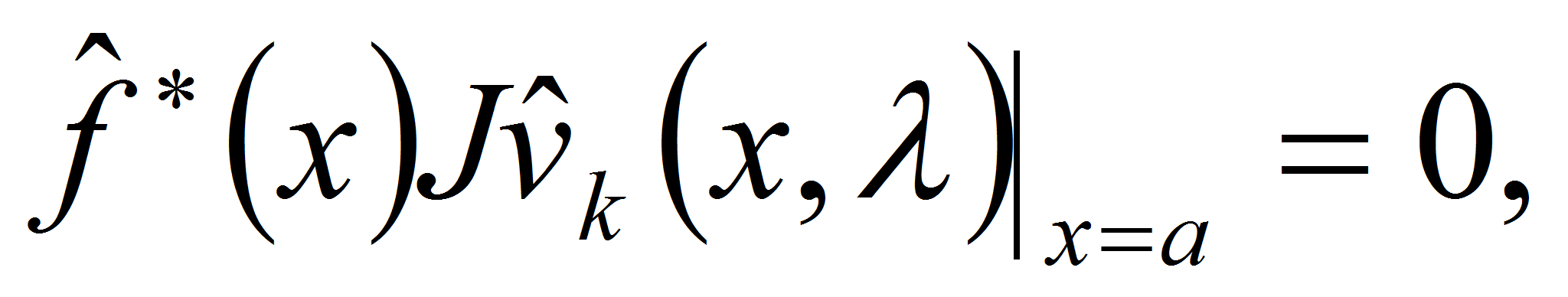какова бы ни была вектор-функция ;

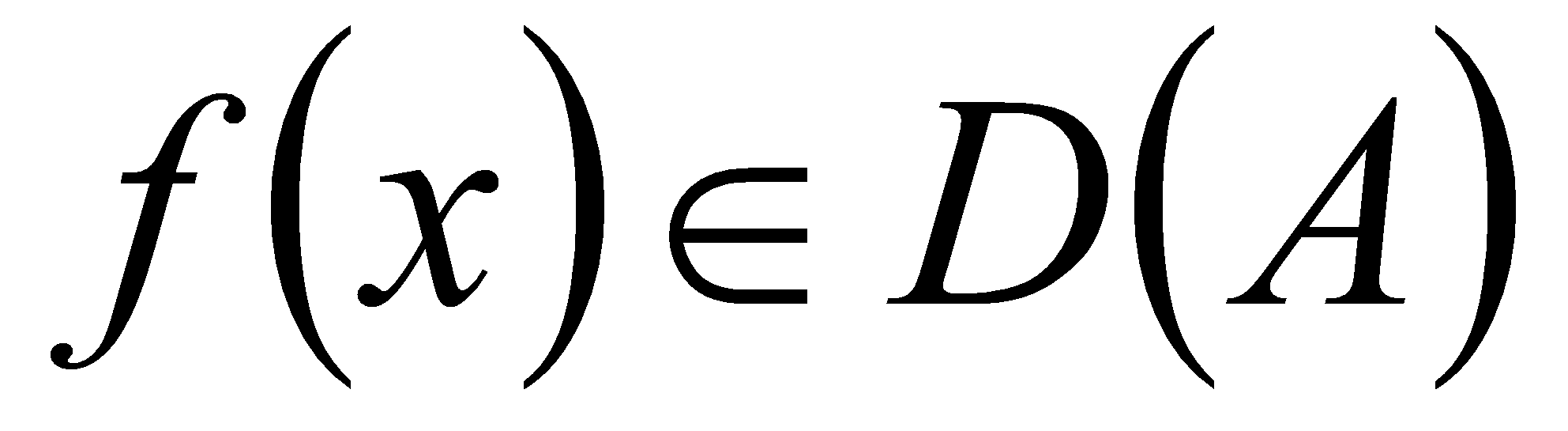3) каждая из вектор-функций 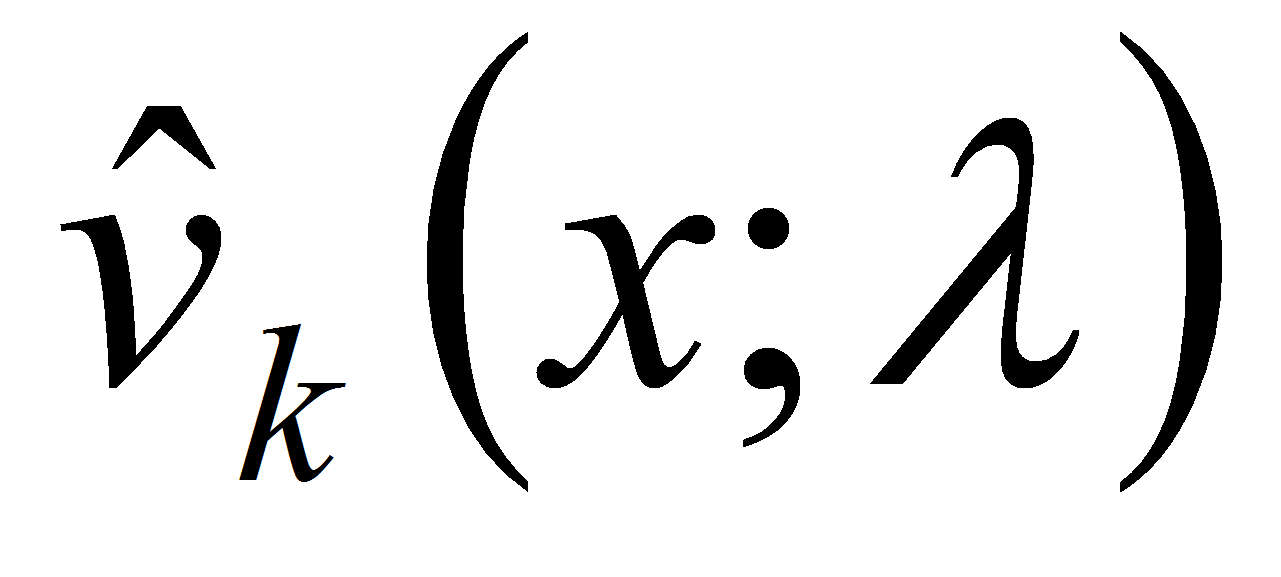при любом фиксированном 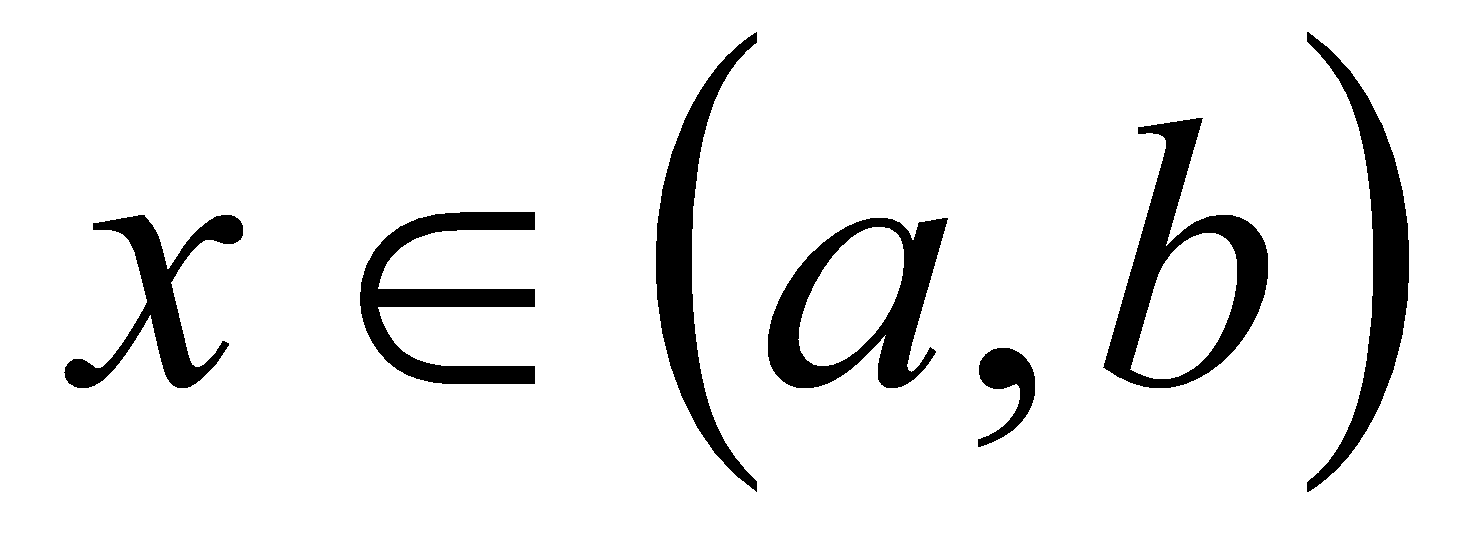удовлетворяет условию Липшица по переменной 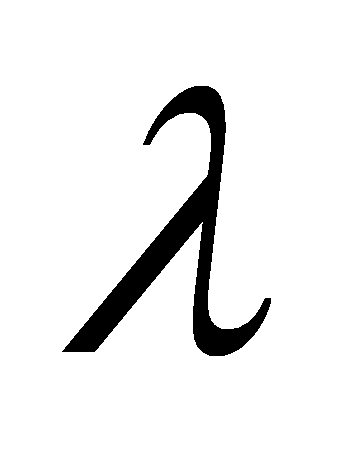на сегменте .

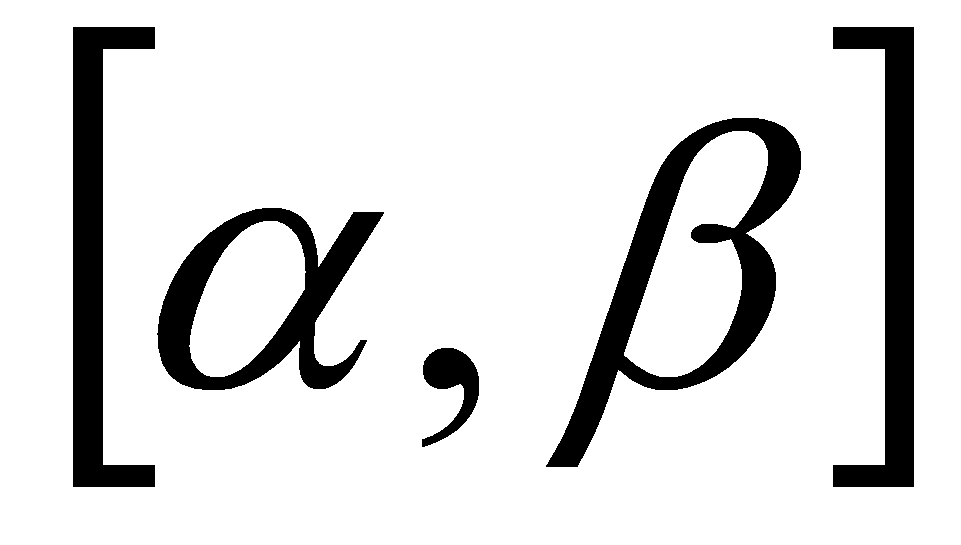Тогда кратность части спектра оператора , заключенной в сегменте , не превосходит .

Замечание 1. Если какой-либо из операторов с минимальной областью определения, порожденных операцией в пространствах и имеет индекс дефекта , то можно опустить условие 1 б) или 2 б), так как его выполнение обеспечивается в этом случае условием 1 а) или 2 а).

Замечание 2. В условиях теоремы 2 ранг матрицы не превосходит .

Литература:

1. Наймарк М.А. Линейные дифференциальные операторы. – М.: Наука, 2010. – 528 с.
2. Филиппенко В.И. Оценка кратности спектра квазидифференциального оператора // Исследования по математическому анализу, математическому моделированию и информатике. – Владикавказ: Владикавказский научный центр РАН и РАО - А, 2007. – С. 86 – 93.
3. Фетисов В.Г., Филиппенко В.И., Козоброд В.Н. Операторы и уравнения в линейных топологических пространствах. – Владикавказ: ВНЦ РАН, 2006. – 432 с.