Значительное место в школьном курсе математики занимают элементы математического анализа, в том числе и пределы функций с раскрытием неопределенностей. Целью изучения в школьной программе этой темы является формирование интеллектуального развития учащихся, формирование качеств мышления, необходимых человеку для свободной ориентации в современном мире; овладение математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования. Но как показывает опыт преподавания учителей в школе, вычисление пределов вызывает большие затруднения у школьников по сравнению с другими темами.Вразделе «Предел функции и непрерывность» заметен высокий уровень научности и строгости понятий предела и непрерывности функции. Раскрытие неопределенностей — методы вычисления пределов функций, заданных формулами, которые теряют смысл в результате формальной подстановки в них предельных значений аргумента, то есть переходят в выражения .

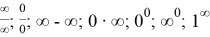
Вопрос решения пределов является достаточно обширным и является объектом интереса современных направлений математики. Существуют десятки нюансов и хитростей, позволяющих решить данный предел. Объектом нашего исследования правила раскрытия неопределенностей и правила Лопиталя. Можно привести огромный список литературы, в которой изучаются пределы, способы их вычислений. Вместе с тем, при изучении нами различных публикаций по данной тематике выявлена относительная недостаточность данных в курсе школьной математики. В основном материалы представлены для изучения в высших учебных заведениях. В курсе же 10 класса отводится всего лишь 10 часов на раздел. Поэтому предлагаю методические рекомендации по методике раскрытия неопределенностей при вычислении пределов функции.

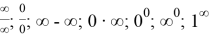
1. Предел функции

Вспомним определения:

1) Число L называется пределом функции f(x) при x a , если для любого сколь угодно малого числа найдется число N такое, что при . Символически записывают так:

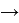
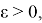
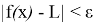
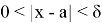
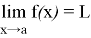
2) Число L называется пределом функции f(x) при x , если для любого сколь угодно малого числа найдется такое число , что для любого x>N выполняется неравенство Пишут:

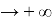
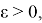
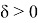
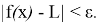
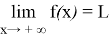
Отыскание предела функции по определению — это довольно трудоемкий процесс. Поэтому на практике удобнее пользоваться следующими теоремами о пределах.

Теорема. Если функции имеют пределы при

, то существует

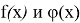
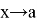
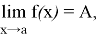
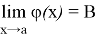
1) предел суммы этих функций, причем

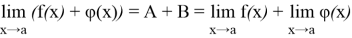
2) предел произведения этих функций, причем

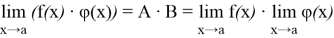
3) предел их отношения

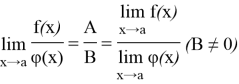
4) постоянный множитель можно выносить за знак предела:

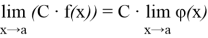
Некоторые методы и приемы вычисления пределов.

Пример 1.Найти предел:

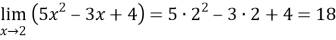
Пример 2.Найти предел:

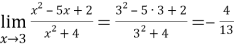
Пример 3.Найти предел:

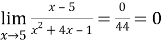
Пример 4.Найти предел:

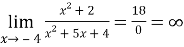
2. Раскрытие неопределенностей

Нужно иметь в виду, что знак — это только символ для обозначения бесконечно большой величины. Он не обладает свойствами числа и в арифметических действиях не участвует. В следствие этого возникают различного рода неопределённости. Основные виды неопределенностей:

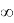
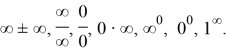
Вычисление пределов в этих случаях называют «раскрытием неопределенности». Вышеуказанные теоремы для бесконечных пределов неверны. Для вычисления предела — «раскрытие неопределенностей», предварительно преобразовывают выражения.

Пример 1.Найти предел:

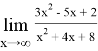
Решение. Теорему о пределе частного применять нельзя, так как числитель и знаменатель дроби конечного предела не имеют. Имеем неопределенность вида . Для избавления от неопределенности вынесем за скобки в числителе и знаменателе дроби переменную в старшей степени:

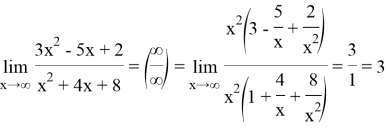
Пример 2.Найти предел:

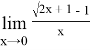
Решение. Числитель и знаменатель дроби при х 0 стремятся к нулю, следовательно, имеем неопределенность вида . Для того, чтобы вычислить предел, перенесем иррациональность в знаменатель, умножив для этого числитель и знаменатель дроби на . Тогда

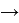
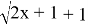
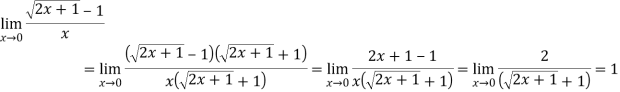
Пример 3.Найти предел:

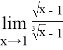
Решение.Неопределенность здесь можно раскрыть, сделав замену переменной , тогда

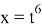
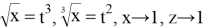
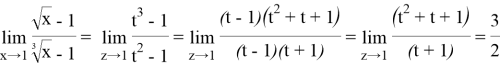
Пример 4.Найти предел:

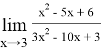
Решение. При вычислении данного предела применять теорему о пределе частного нельзя, так и числитель, и знаменатель равны 0. Воспользуемся разложением многочленов числителя и знаменателя на множители по формуле где — корни квадратного трехчлена

. Тогда

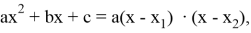
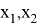
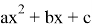
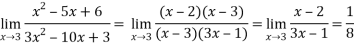
3. Замечательные пределы

Пределы функций, в которых участвуют тригонометрические выражения, обычно сводятся к первому замечательному пределу

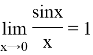
Также используют несколько его следствий:

, , , ,

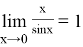
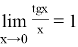
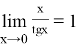
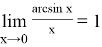
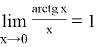
Пример 5.Найти предел:

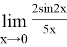
Решение. Для избавления неопределенности воспользуемся первым замечательным пределом

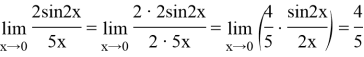
Пример 6.Найти предел:

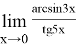
Решение. Произведя следующие преобразования, имеем

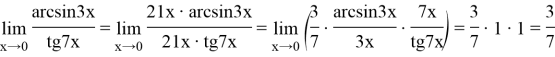
Пример 7. Найти предел:

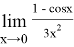
Решение. Так как , то

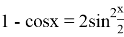
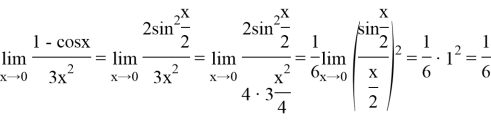
Пример 8.Найти предел:

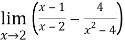
Решение. В этом примере получаем неопределенность вида . Приведем выражение под знаком предела к общему знаменателю.

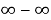
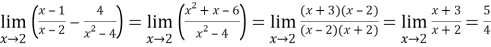
Пример 9. Найти предел:

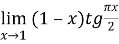
Решение. Неопределенность вида сведем к неопределенности , тогда

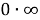
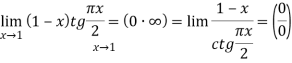
Сделаем замену переменных , тогда и

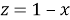
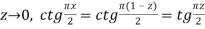
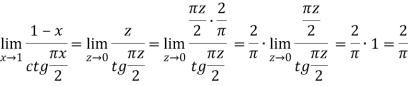
Заключение

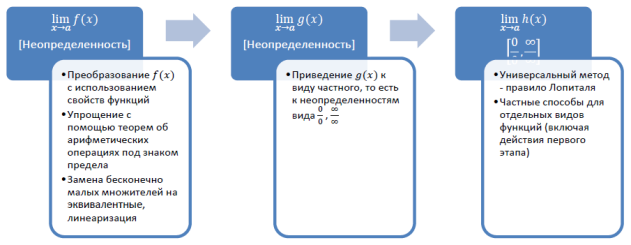
Таким образом, в процессе раскрытия неопределенностей можно выделить следующие основные этапы:

1) подготовка выражения под знаком предела к устранению неопределенности путем применения преобразований;

2) переход (в случае необходимости) к неопределенности или — переход от одной функции к другой.

Литература:

1. Абылкасымова А. Е., Кучер Т. П., Корчевский В. Е., Жумагулова З. А., Алгебра и начала анализа: Учебник для 10 класса ЕМН, Алматы: Мектеп, 2019;
2. Темиргалиев Н., Введение в математический анализ, Астана, 2015;
3. Круглов Е. В., Мамаева Н. А., Таланова Е. А., Некоторые приемы вычисления пределов Нижний Новгород, 2018;
4. Матвеева Т. А., Рыжкова Н. Г., Математический анализ, Екатеринбург, 2017;
5. Самочернова Л. И., Высшая математика, Томск, 2005;
6. Альпин Т. Ю., Егоров А. И., Кашаргин П. Е., Сушков С. В., Практические занятия по математическому анализу, Казань, 2013.