Разработаны математические модели электрического поля активной зоны нового электромагнитного датчика расхода с кольцевыми каналами и с плоскими электродами в трехмерном приближении и установлено, что с увеличением ширины кольцевого канала неравномерность весовой функции возрастает, искажение потока воды в трубопроводе по осевой координате не влияет на выходной сигнал, а при угле между плоскостями электродов, равном 70 ^0– 80 ⁰ , весовая функция становится равномерной и выходной сигнал не зависит от искажения потока воды также и по радиальной координате. Показано, что для получения весовой функции электромагнитных датчиков расхода с чередующимися полюсами необходимо считать кольцевые каналы изолированными друг от друга и в каждом кольцевом канале установлены плоские электроды, координаты которых зависят от формы выполнения каналов.

Ключевые слова: математическая модель, электромагнитный датчик расхода, кольцевой канал, активная зона, искажение симметрии потока воды, весовая функция.

При исследовании электромагнитных процессов в измерительных каналах электромагнитных датчиков расхода (ЭДР) целесообразно пользоваться весовой функцией, характеризующей удельный вклад каждой точки канала в создание выходного сигнала между электродами. Эта функция позволяет установить зависимость выходного сигнала от конструктивных параметров канала, формы и положений электродов и длины изоляционного слоя. Аналитическое выражение для весовой функции ЭДР в трехмерном приближении с точечными электродами получено Вельтом [1]. Выражение весовой функции ЭДР с кольцевым каналом и с плоскими электродами в литературе не приводится.

Весовая функция ЭДР с кольцевым каналом в настоящей работе найдена путем решения следующей классической задачи: в кольцевом канале бесконечной длины между коаксиально расположенными полыми цилиндрами шириной по направлению оси (рис.1) движется электропроводящая жидкость, в частности вода. Электроды ЭДР имеют координаты а изолирующие слои нанесены на поверхностях наружного и внутреннего цилиндров с координатой [2]. Магнитное поле создается в радиальном направлении и в общем случае неравномерно.

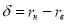
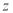
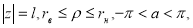
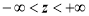
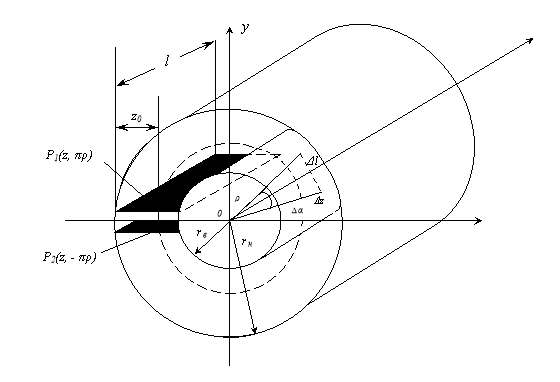
Рис. 1. Вид кольцевого канала ЭДР

Будем считать, что поток воды имеет только одну составляющую и выполняется следующие граничные условия:

(1)

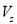
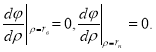
Рассмотрим элемент кольцевого канала , на который наложено магнитное поле с индукцией . Пусть в результате движения потока воды в кольцевом канале возникает электрическое поле. Для некоторых точек элементарной области данного электрического поля дипольный момент можно представит в виде:

(2)

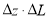
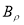
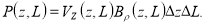
Разность потенциалов между выбранными точками и находится как

(3)

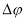
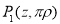
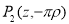
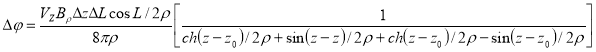
В выражение (3) вместо подставим . Тогда среднее значение разности потенциалов в зоне электродов соответственно будет

, (4)

где — весовая функция для кольцевого канала с шириной , расстоянием между электродами и длиной последнего . После интегрирования для весовой функции будем иметь следующее:

, (5)

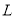
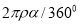
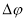
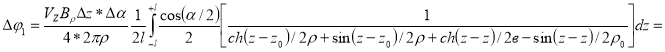
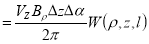
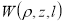
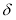
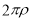
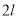
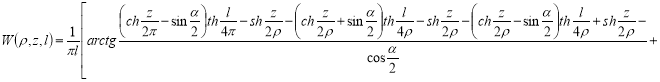
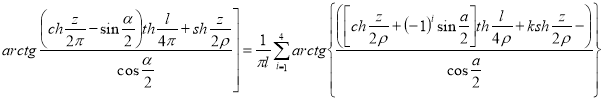
где

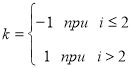
Поверхностный интеграл от весовой функции (5) равен расстоянию между электродами

, (6)

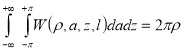
а объемный интеграл от весовой функции (5) равен среднему значению расстояния между электродами

. (7)

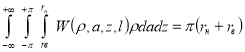
С помощью формулы (5) не трудно определить величину входного сигнала ЭДР при любом распределении магнитной индукции и профиля скоростей потока воды в кольцевом канале:

. (8)

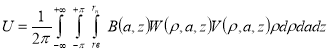
Формула (8) представляет собой статическую характеристику ЭДР с кольцевым каналом. Вычислит весовую функцию ЭДР с чередующимися магнитными полюсами весьма сложная задача. Это объясняется тем, что координаты и в канале изменяются в широких пределах, к тому же угловая координата меняет свой знак. Весовая функция для таких датчиков также зависит от их конкретной конструкции.

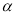
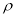
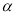
Для ЭДР, в котором чередующиеся магнитные полюса образуются наконечниками в виде архимедовой спирали [2], сигнал проще определить с помощью выражения для расстояния между основными электродами

,

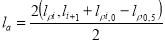
где

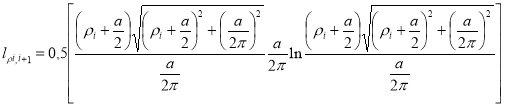
Длина спирали с радиус-вектором ; - шаг спирали.

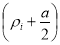
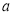
Для определения весовой функции ЭМР, в которых чередующиеся магнитные полюса создаются введением в магнитную систему полых ферромагнитных цилиндров [3], примем следующие допущения:

1. Кольцевые каналы изолированы друг от друга.
2. В каждом канале установлены плоские электроды, координаты которых зависят от формы выполнения каналов.

С учетом этих допущений разработана следующая методика определения выходного сигнала:

1. Определяется весовая функция для каждого кольцевого канала в отдельности.
2. Выходной сигнал записывается для каждого канала.
3. Выходной сигнал ЭДР с чередующимися магнитными полюсами находится арифметическим суммированием сигналов кольцевых каналов.

С учетом вышеперечисленного запишем выражение для выходного сигнала ЭДР с чередующимися магнитными полюсами

(9)

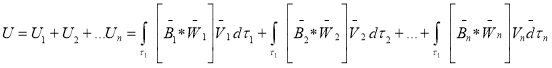
где и - соответственно выходное напряжение, магнитная индукция, весовая функция, скорость потока воды и объем для - ого кольцевого канала: - количество кольцевых каналов.

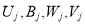
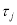
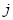
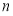
Для подтверждения значений полученных весовых функций проведены экспериментальные исследования активной зоны ЭДР. Для этого изготовлены макетные образцы кольцевого канала. Полые цилиндры выполнены из органического стекла с тем, чтобы можно было зафиксировать положение исследуемого элементарного объема. Расстояние между коаксиальными цилиндрами, измерялось путем использования цилиндров различного диаметра. Электроды выполнены в виде плоских пластин из меди шириной, равной ширине кольцевого канала между цилиндрами и укреплены на изоляционной перемычке, соединяющей между собой коаксиально цилиндры по всей длине. Для исследования характера изменения вклада точек канала в выходной сигнал угол между плоскостями электродов изменялся до 90 ⁰ . Для воспроизведения граничных условий на концах кольцевого канала длина внутреннего цилиндра выбрана меньше наружного.

Как известно [1, 6–8], весовую функцию можно представить как отношение градиента потенциала в рассматриваемой точке активной зоны канала ЭДР к напряжению на электродах:

. (10)

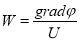
Это отношение позволяет определить экспериментальным путем весовую функцию по методу моделирования электрического поля в проводящей среды. Моделью служит кольцевой канал датчика, заполненный водопроводной водой.

Для выполнения измерений весовой функции использовался следующий способ моделирования электрического поля [1]. Градиент потенциала в заданном объеме воды задавался введением в эту область специального зонда, состоящего из двух медных изолированных друг от друга и от окружающий среды (воды) проводников, контактирующих с водой только своими концами [4, 5, 9, 10]. Зонд питается от источника переменного тока напряжением 10 В. При этом измерялась разность потенциалов между электродами и точкой, потенциал которой равен нулю.

Воспроизводимый таким зондом градиент потенциала определяется по формуле

(11)

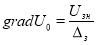
где - разность потенциалов между концами зонда, контактирующими с водой в кольцевом канале;

- расстояние между концами зонда.

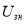
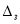
Измерения потенциалов на электродах производились компенсационным способом [1].

По данным измерений вычислены значения весовой функции по формуле (10). На рис.2 представлена весовая функция в зависимости от координат и . Из графиков видно, что вычисленные значения весовой функции по формуле (5) (сплошные линии) весьма близко совпадают с измеренными соответствующими значениями (пунктирные линии).

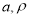
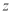
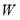
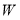
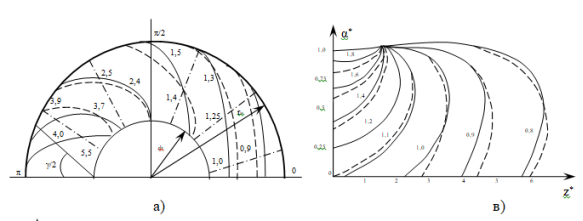
Рис. 2. Изолинии весовой функции, полученные аналитически (сплошные линии) и экспериментально (пунктирные линии):

а) в центральном сечении при линии при угле между электродами, равной 70 ^0– 80 ⁰ .

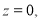
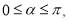
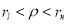
б) в тонком кольцевом сечении с радиусом

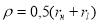
в) вдоль оси при

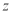
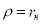
г) в центральной сечение при .

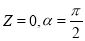
Полученные кривые показывают, что в зоне между электродами значения весовая функции в осевом направлении не меняются, с увеличением ширины кольцевого канала неравномерность весовой функции возрастает, а при угле между плоскостями электродов, равном 70–80 ⁰ , она становится равномерной.

Таким образом, в результате проведенных исследований можно сделать следующее заключение: Искажение потока воды в трубопроводе по осевой координате не влияет на выходной сигнал ЭДР с кольцевыми каналами, а при угле между плоскостями электродов, равном 70–80 ⁰ , выходной сигнал не зависит от искажения потока воды также и по радиальной координате.

Литература:

1. Вельт И. Д. Разработка общих принципов проектирования электромагнитных расходомеров и средств метрологического обеспечения. Дисс… д.т.н. Москва., ВНИИФТРИ, 1987. — 312 с.
2. Амиров С. Ф. Электромагнитные датчики параметров движения для систем управления гидромелиоративными объектами. Дисс….. д.т.н. Российская Федерация, Астрахань, АГТУ, 1997.- 375 с.
3. Заявка на патент РУз № IAP 20120180. Электромагнитный преобразователь расхода. / Амиров С. Ф., Атауллаев А. О., Турдибеков К. Х., Жураева К. К., Атауллаев Н. О. -Заявлено в 14.05. 2012 г.
4. Амиров С. Ф., Болтаев О. Т. Математическая модель трансформатора тока с нелинейной кривой намагничивания // Актуальные проблемы инновационных технологий на железнодорожном транспорте. 25 марта 2011. — Тошкент, 2011. — С. 229–331.
5. Amirov S. F., Boltaev O. T., Axmedova F. A. New created mathematical models of movable screens and a scatter parameters converters // Jour of Adv Research in Dynamical & Control Systems, Vol. 12, Special Issue-02, 2020. pp. 122–126
6. Amirov S. F., Boltayev O. T., Axmedova F. A. Calculation of Magnetic Chains with Mobile Screens // International Journal of Advanced Research in Science Engineering and Technology. India. — № 6, Issue 5, May 2019 — pp. 9243–9245.
7. Амиров С. Ф., Атауллаев А. О., Болтаев О. Т. Исследование двухконтурных магнитных цепей датчиков с распределенными параметрами. Материалы II Международной научно-технической конференции «Проблемы получения, обработки и передачи измерительной информации», посвященной 90-летию со дня рождения профессора Зарипова М. Ф./Уфимск. Гос. Техн. Ун-т: РИК УГАТУ, 2019. –С.127–131.
8. Амиров С. Ф., Суллиев А. Х., Болтаев О. Т., Шарапов Ш. А. Исследование магнитных цепей бипараметрических резонансных датчиков// ТошТЙМИ Ахбороти. — Тошкент, 2010. — № 3. — 49–54 б.
9. Амиров С. Ф., Жураева К. К., Болтаев О. Т. Исследование магнитных цепей с распределенными намагничивающими обмотками// ТошТЙМИ Ахбороти. — Тошкент, 2019. — № 1. — 100–106 б.
10. Мерганов Аваз Мирсултанович, Хаджимухаметова Матлюба Адиловна, Урманова Зарина Абдивохид Кизи К АНАЛИЗУ ГРУЗОПОТОКА ТАРНО-УПАКОВОЧНЫХ ГРУЗОВ ПЕРЕРАБАТЫВАЕМЫХ НА ЖЕЛЕЗНОДОРОЖНЫХ СКЛАДАХ // Universum: технические науки. 2019. № 10–1 (67). URL: https://cyberleninka.ru/article/n/k-analizu-gruzopotoka-tarno-upakovochnyh-gruzov-pererabatyvaemyh-na-zheleznodorozhnyh-skladah (дата обращения: 11.07.2020).