В данной статье рассказывается о создании метода по обеспечению единства измерений, а также некоторых основных понятий, связанный с метрологией.

Ключевые слова: измерения, прибор, датчик, обработка, метрология, метод, расчет, точность, погрешность.

В наше время широкое развитие получает разработка роботов и измерительных приборов в целом. В связи с этим существует потребность проведения измерений для последующего внедрения технологий в проект. Но так как в данном случае важным параметром является точность, то нужны приборы, отвечающие данному критерию, так как ошибки могут привести к фатальным последствиям.

В связи актуальностью темы развития проектирования роботов, целью исследования стала разработка некого универсального метода, который бы помог определиться с выбором приборов на основе полученных данных.

Разработанный метод должен являться неким сборником простых и проверенных методов, который позволит быстро и качественно проводить испытания, делать выводы на основе полученных данных о внедрении тестируемого прибора/датчика в робота или же измерительную систему. Поэтому начнем со знакомства с основами, которые помогли в создании метода.

Наука, которая занимается вопросами о проведении и способах измерений, а также проведением мероприятий по улучшению качества и точности измерений, и об единстве измерений в целом, называется метрологией. Данная наука состоит из трех разделов:

− Теоретического (занимается разработкой методов для проведения испытаний, а также изучением основных элементов в измерительной технике);

− Законодательного (занимается разработкой правовой основы для проведения испытаний, калибровочных и поверочных работ, которая способствует улучшению качества измерений);

− Практического (занимается проверкой разработок двух предыдущих разделов).

Есть также основные понятие, такие как: точность, погрешность, средства измерений, классы точности и т. д.

Точность — величина, характеризующая степень приближенности измеренного значения к истинному.

Погрешность — величина, характеризующая отклонение измеренного значения от истинного значения. Существуют разные виды погрешности, но познакомимся с основными:

− Абсолютная погрешность — разность между истинным и измеренным значениями величины;

− Относительная погрешность — значение, равное отношению абсолютной погрешности к истинному значению;

− Приведенная погрешность — Значение, равное отношению абсолютной погрешности к нормирующему значению;

− Случайная погрешность — вид погрешности, возникающий произвольно при проведении испытаний;

− Систематическая погрешность — погрешность, изменяющаяся по определенному закону;

− Прогрессирующая погрешность — погрешность, меняющаяся с течением времени;

− Грубая погрешность — погрешность по причине упущений или недосмотра испытателем при проведении работ либо из-за неисправности аппаратуры [2, c. 546].

Класс точности — мера прибора, определяемая пределами основных и дополнительных погрешностей, а также другими факторами, влияющими на точность измерений [3, с. 1].

Нормированное значение погрешности — мера, используемая для определения вносимой погрешности в результаты измерений.

Измерение — совокупность операций, определяющих зависимость между величинами. Существует несколько типов измерений:

− Прямое сличение — сравнение, при котором значения тестируемого прибора сравниваются со значениями эталонного прибора;

− Косвенное измерение — поиск функциональных зависимостей, проведение расчетов, основанных на данной зависимости, это приводит к нахождению реального значения;

− Проверочные схемы — схемы, служащие для минимизации неточностей в процессе измерений [1, с. 4].

При проведении испытаний лучше всего использовать метод прямых сравнений, потому как данный вид измерений является наиболее простым в реализации и наглядным.

Перейдем к методу. Проводятся измерения во всем диапазоне измерений определяемой величины. Для каждого значения эталонного датчика , i=1...N (или принимаемого за эталонный) проводится серия измерений ( ), j=1...M датчиком, предназначенным для калибровки. Определяется средние значения для каждого ( ) и величина разброса (отклонения дельта). Строится зависимость = F(x), которая определяет значения показаний калибруемого датчика от «эталонных — истинных» значений. Далее вычисляется обратная зависимость = F (Y), которая переводит показания исследуемого калибруемого датчика в истинные (эталонные) значения.

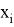
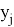
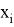
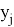
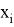
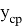
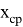
После проведения эксперимента производится обработка полученных данных. Результатом данной обработки является то, что шкала тестируемого прибора будет приводиться к шкале эталонного.

Метод обработки данных основывается на математической статистике, поэтому мы используем в расчетах среднее значение, среднеквадратическое отклонение, дисперсия, коэффициент Стъюдента и т. д.

Для лучшего понимания, рассмотрим метод по шагам:

1. Вычисление среднего значения измерения в каждой точке;
2. Вычисление отклонения дельты с учетом систематической погрешности эталонного прибора;
3. Построение линии тренда в виде полинома третьей степени;
4. Вычисление истинного значения за счет коэффициентов, полученных при построении графиков в предыдущем шаге.

Теперь остановимся на каждом шаге поподробнее. Вычисление среднего значения происходит в соответствии с рис. 1.

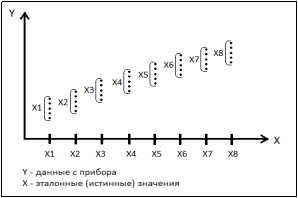
Рис. 1. График расчета среднего значения

Данный расчет производится для того, чтобы узнать среднее значение измерений в каждой точке.

Во втором шаге вычисляется отклонение дельты с учетом погрешности эталонного прибора. Но сперва рассчитывается среднеквадратическое отклонение по формуле:

,

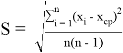
где — измерение в каждой точке, среднее значение в каждой точке, количество измерений. После происходит вычислении самой дельты:

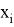
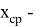
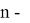
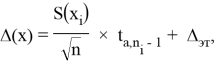
где среднеквадратическое отклонение, количество измерений, коэффициент Стьюдента, погрешность эталонного прибора.

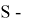
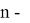
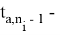
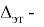
После вычисления дельты получаем , как показано на рис. 2.

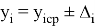
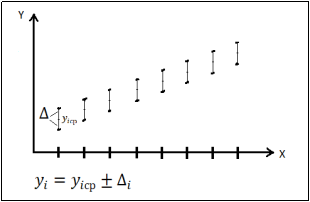
Рис. 2. График поучения значений

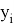
Далее строятся линии тренда полинома 3 степени, формулы которых следующие: , , . Линии тренда графиков показывают коэффициент как для верхнего ( ), так и нижнего ( ) отклонений показаний. Эти коэффициенты используются при поиске истинного значения измерений. Также мы имеем коэффициенты , которые являются калибровочными.

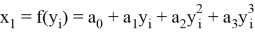
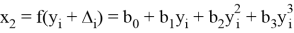
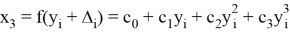
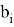
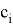
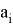
На основе полученных данных можно вычислить истинное значение величины. Приняв за значение «X» в формулах для линий трендов верхнего и нижнего отклонений измеренную величину, получим значения величины с учетом верхнего и нижнего отклонений. Далее происходит расчет истинного значения по формуле: , где значение верхнего отклонения измеренной величины, значение нижнего отклонения измеренной величины.

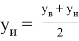
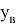
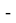
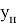
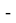
После вышеперечисленных манипуляций происходит расчет погрешности, который также включает в себя методы математической статистики.

Расчет погрешности происходит следующим образом:

1. Рассчитывается среднее значение;
2. Рассчитывается среднеквадратическое отклонение;
3. Производится поиск коэффициента Стьюдента в связи с доверительной вероятностью. Данный коэффициент зависит не только от вероятности, но и количества измерений;
4. Рассчитывается длина доверительного интервала многократных измерений по формуле: , где t — коэффициент Стьюдента, S — среднеквадратическое отклонение;
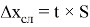
5. Рассчитывается длина доверительного интервала однократных измерений по формуле: , где — доверительная вероятность, — цена деления прибора;
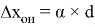
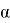
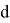
6. Расчет абсолютной погрешности: ;
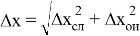
7. Расчет относительной погрешности: ;
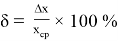
8. Запись результата в виде: .

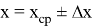
Заключение: Рассмотренный метод является неким сборником наработок в области метрологии. Использование элементов распределения Стьюдента поможет в прогнозировании поведения генеральной совокупности измерений, так как количество произведенных много меньше. Проверка данного метода довольно проста и достаточно наглядна, а расчеты можно производить в программе по обработке таблиц, будь то Microsoft Excel или OpenOffice Calc.

Литература:

1. Методы обработки результатов измерений и оценки погрешностей в учебном лабораторном практикуме / Н. С. Кравченко, О. Г. Ревинская — Томск: Томский политехнический университет, 2017. — 120 с.
2. Руководство по метрологическим приборам и методам наблюдений / Всемирная Метеорологическая Организация — 2017. — 1386 с.
3. ГОСТ 8.401–80. Государственная система обеспечения единства измерений (ГСИ). Классы точности средств измерений. [Текст] введ. 1981–06–30 — Москва: Стандартинформ, 2010–10 с.