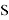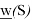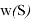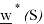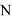В теории кооперативных игр с трансферабельными полезностями особое место занимают решения, основанные на эксцессах коалиций. Для нахождения решений подобных N-ядру, требуются нахождение лексикографически минимального вектора среди всех векторов эксцессов, упорядоченных по неубыванию [1]. Это создает множество проблем, поскольку поиск такого вектора является крайне нетривиальной задачей, и часто такие решения находят вручную. В данной статье представлен программный метод нахождения эксцессоподобных решений, основанный на функции лексикографической разницы.

Ключевые слова: кооперативные игры, эксцессоподобные решения, N-ядро, эксцесс коалиции, лексикографическая разница, метод поиска решений.

Существует множество способов программного поиска эксцессоподобных решений — метод перебора, решение задачи линейного программирования [2] и другие. Но семейство кооперативных игр огромно, и во многих случаях известные методы решений могут оказаться слишком трудозатратными или же попросту неподходящими для конкретного вида кооперативной игры.

Поиск эксцессоподобных решений достаточно важная задача в силу особенности таких решений. Данные решения интересны тем, что минимизируют неудовлетворенности коалиций, что позволяет в некоторых случаях найти более справедливые выигрыши для игроков.

В данной работе будет рассматриваться поиск решений, которые дают лексикографически минимальный вектор эксцессов коалиций кооперативной игры. Данный метод подойдет для поиска N-ядра, SM-ядра [3], интервального N-ядра [4] и других подобных решений.

Эксцессом коалиции кооперативной игры будем называть

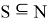
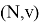
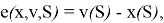
где , — выигрыш коалиции.

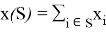
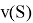
Метод минимизации лексикографической разницы

Идея данного метода заключается в минимизации функции лексикографической разницы вектора эксцессов коалиций предыдущего решения с вектором эксцессов текущего. Под лексикографической разницей в данной работе понимается следующая функция:

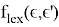
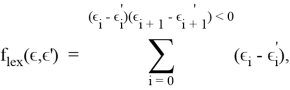
где , — компоненты векторов и соответственно.

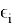
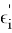
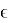
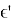
Рассмотрим задачу подробнее:

— вектор эксцессов коалиций кооперативной игры, упорядоченный по невозрастанию, от решения .

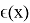
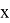
В данном случае — решение игры, принадлежащее некоторому множеству . Это может быть множество допустимых решений, множество дележей или какое-либо другое множество, характеризующее искомое решение.

— компоненты вектора .

— лексикографически минимальный вектор эксцессов, упорядоченный по невозрастанию, на -ом шаге.

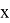
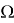
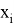
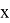
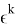
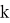
Перейдем к самому алгоритму. На 0 шаге:

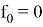
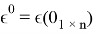
На 1 шаге:

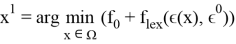
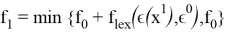
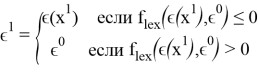
На -ом шаге:

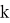
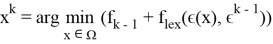
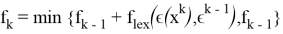
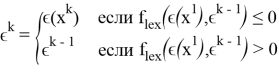
Критерий останова:

Алгоритм следует закончить на -ом шаге при , где — заданная точность, или же после достижения определенного количества шагов. Решением будет вектор .

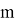
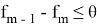
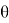
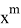
Неплохим методом для решения такой задачи показался метод последовательного программирования наименьших квадратов, поскольку он последовательно решает задачи квадратичного программирования, аппроксимирующие основную задачу оптимизации [5].

Пример

Рассмотрим интервальную кооперативную игру, представленную в таблице 1.

Таблица 1

Пример интервальной кооперативной игры

N-ядро для нижней граничной игры:

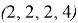
N-ядро для верхней граничной игры:

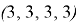
Интервальное N-ядро:

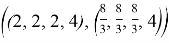
SM-ядро для нижней граничной игры:

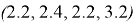
SM-ядро для верхней граничной игры:

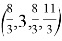
Интервальное SM-ядро:

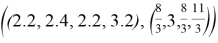
Результаты работы алгоритма:

N-ядро для нижней граничной игры: .

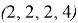
N-ядро для верхней граничной игры: .

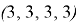
Интервальное N-ядро:

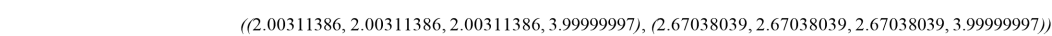
SM-ядро для нижней граничной игры: .

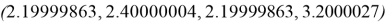
SM-ядро для верхней граничной игры: .

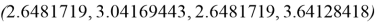
Интервальное SM-ядро:

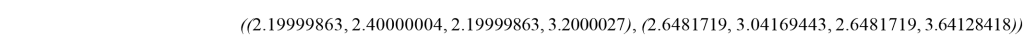
Литература:

1. Печерский С. Л., Яновская Е. Б. Кооперативные игры: решения и аксиомы. М.: Европейский университет в Санкт-Петербурге, 2004.
2. Сергей В. Бритвин, Светлана И. Тарашнина, Алгоритмы нахождения пред-N-ядра и SM-ядра в кооперативных ТП-играх, МТИП, 2013, том 5, выпуск 4, 14–32
3. Tarashnina S. I., The simplified modified nucleolus of a cooperative TU-game //Top, 2011, T.19, C. 150–166.
4. Elena B. Yanovskaya, The Nucleolus and the $\tau$-value of Interval Games // Contributions to Game Theory and Management, 2010, Volume 3, P.421–430.
5. Sequential quadratic programming, https://en.wikipedia.org/wiki/Sequential_quadratic_programming