В статье рассматривается моделирование непрерывных случайных величин, вычисление параметров случайных величин по выборке, изучение свойства состоятельности выборочных оценок средствами языка программирования R.

Ключевые слова: моделирование, непрерывная случайная величина, язык R.

Пользуясь средствами языка программирования «R«, рассмотрим процесс реализации на ЭВМ и исследования на точность алгоритма моделирования непрерывной случайной величины (НСВ), распределенной по логнормальному закону L(m, σ):

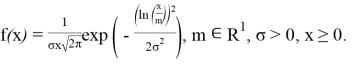(1)

Метод моделирования НСВ ξ с законом распределения L(m, σ) основан на связи логнормального распределения с нормальным N(µ, σ), а также последнего с равномерным R(a, b) распределением [3, стр. 61]:

(2)

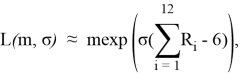
Реализуем на языке программирования R функцию LogNorm для моделирования n независимых случайных чисел, имеющих логнормальное распределение:

Рассмотрим результат работы функции LogNorm с параметрами µ = 0.6, σ = 1 при моделирования n = 100 и n = 1000 независимых случайных чисел:

> ksi <- LogNorm(n, 0.6, 1);

На рис. 1–2 представлены графики теоретической плотности вероятности логнормального распределения и гистограммы плотности относительных частот для результатов моделирования n = 100 и n = 1000 НСВ, а на рис. 3–4 отображены графики эмпирической и теоретической функции распределения для соответствующих объёмов выборки. Можем заметить, что с увеличением объема выборки гистограмма плотности относительных частот стремится к полигону распределения вероятностей, а эмпирическая функция распределения — к теоретической.

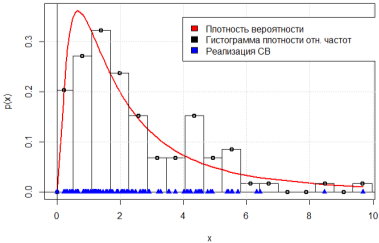
Рис. 1. График теоретической плотности вероятности и гистограмма плотности относительных частот, n = 100

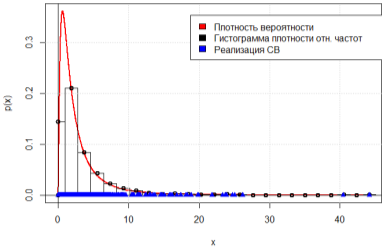
Рис. 2. График теоретической плотности вероятности и гистограмма плотности относительных частот, n = 1000

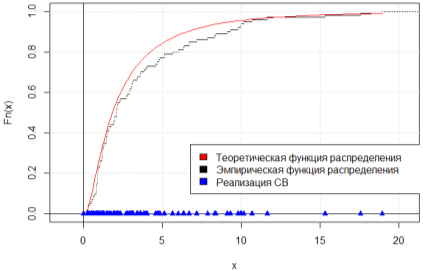
Рис. 3. Графики эмпирической и теоретической функции распределения, n = 100

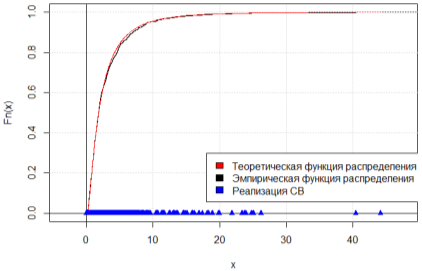
Рис. 4. Графики эмпирической и теоретической функции распределения, n = 1000

Будем использовать следующий программный код для вычисления выборочных оценок параметров случайных величин по выборке и по интервальному статистическому ряду:

a) По выборке:

Среднее: > tildaX <- mean(log(ksi)); print(tildaX);

Дисперсия: > vd <- var(log(ksi)); print(vd);

Дисперсия (исправленная выборочная):

> MeanV <- function(N, n, X) { return (sum(n*X)/N); }

> SS0<-MeanV(N-1, 1, log(ksi)*log(ksi))-N*(tildaX*tildaX)/(N-1);

> print(SS0);

Среднее квадратическое отклонение: > S<-sqrt(SS0); print(S);

б) По интервальному статистическому ряду:

Cтроим доверительные интервалы для математического ожидания и дисперсии с надежностью γ = 0.95:

Чтобы убедиться в состоятельности выборочной оценки математического ожидания, реализуем средствами языка программирования «R» решение следующих задач: построить график стремления выборочной оценки параметра распределения к параметру распределения по вероятности с увеличением объема выборки n; построить линию параметра; построить доверительные границы, используя неравенство Чебышева. Реализацию решения выполняет следующий программный код:

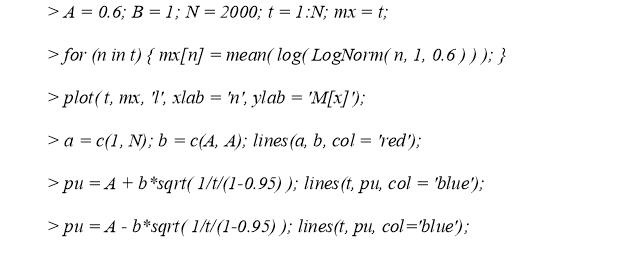
Графический результат для объёма выборки n = 2000 приведён на рис. 5. На его основании можно утверждать, что с увеличением объёма выборки выборочная оценка математического ожидания стремится по вероятности к теоретическому математическому ожиданию распределения.

Для реализации решения задачи статистического моделирования на ЭВМ непрерывных случайных величин средствами языка программирования «R» на примере логнормального распределения были использованы следующие встроенные функции языка:

– runif(n) — моделирование n равномерно распределенных случайных величин от 0 до 1;

– rep(0, n) — создание вектора из n нулей;

– log(x) — вычисление натурального логарифма числа x;

– sqrt(x) — вычисление квадратного корня числа x;

– mean(x) — вычисление математического ожидания вектора х;

– var(x) — вычисление дисперсии вектора x;

– exp(x) — вычисление экспоненты числа x;

– sum(x) — вычисление суммы элементов вектора x.

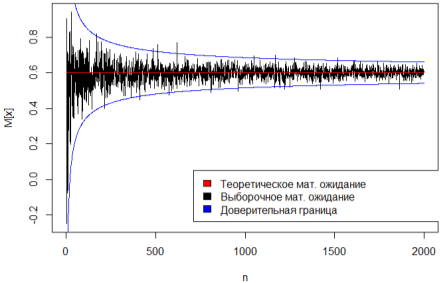
Рис. 5. График сходимости выборочной оценки к параметру распределения, n=2000.

Литература:

1. Лобач В. И. Имитационное и статистическое моделирование: Практикум для студентов мат. и экон. спец. / В. И. Лобач, В. П. Кирлица, В. И. Малюгин, С. Н. Сталевская. — Минск: БГУ, 2004. — 189 с.
2. Харин Ю. С., Степанова М. Д. Практикум на ЭВМ по математической статистике. — Минск: Университетское, 1987. — 304 с.
3. Хастингс Н., Пикок Дж. Справочник по статистическим распределениям. — М.: Статистика, 1980. — 95 с.