В статье рассматривается актуальная для практики методика, которая, используя данные гидрогазодинамических исследований при нелинейных законах фильтрации, позволяет предложить полиномиальный закон в произвольной степени, из которого как частный случай вытекает линейный закон Дарси и двучленный закон Форхгеймера.

Ключевые слова: закон Дарси, закон Форхгеймера, закон Барри-Конвея, число Рейнольдса, проницаемость, аппроксимация.

The article discusses a methodology that is relevant for practice, which, using the data of hydro-gas-dynamic studies with nonlinear filtering laws, allows us to propose a polynomial law to an arbitrary degree, from which, as a special case, the linear Darcy law and the two-term Forchheimer law follow.

Keywords: Darcy law, Forchheimer law, Barry-Conway law, Reynolds number, permeability, approximation.

Как известно, закон Дарси имеет вид [1]:

(1)

Однако дальнейшие исследования показали, что закон Дарси не универсален и имеет свои границы применимости. В статье [2] для уменьшения погрешностей закона Дарси при больших скоростях введен поправочный множитель , с помощью которого закон фильтрации флюидов для больших скоростей представлен в виде:

(2)

Форхгеймер предложил двучленный закон фильтрации [1]:

(3)

где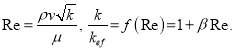

При больших градиентах давления двучленный закон Форхгеймера также дает погрешность. В связи, с чем Р. Д. Барри и М. В. Конвей [3, 4, 5] предложили новую модель, содержащую, кроме параметров , два дополнительных параметра :

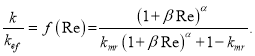(4)

Здесь параметр может принимать значения от нуля до единицы включительно. Из формулы (4) видно, что, если и показатель степени то (4) приводит к классическому уравнению Форхгеймера (3). Однако же, если то (4) приводит к линейному закону Дарси (1).

По закону Барри-Конвея эффективная проницаемость асимптотически падает до некоторого минимального уровня, а по закону Форхгеймера и Куршина А. П. [6] падает до нуля, что по представлениям Р. Д. Барри и М. В. Конвея является неправильным. Они экспериментально доказали, что пропускная способность пористой среды, количественно определяемая эффективной проницаемостью , уменьшается с ростом фильтрационного числа Рейнольдса по определенному закону.

Несмотря на то, что наиболее естественной зависимостью для всех проницаемых сред служит закон Барри-Конвея (4), однако недостатком этого закона является то, что непосредственно применить его для определения параметров на основе результатов гидрогазодинамических исследований скважин весьма затруднительно.

В связи с этим возникает актуальная для практики задача преобразовать закон Барри-Конвея (4) так, чтобы модифицированный закон позволял строить удобные для обработки данные гидрогазодинамических исследований.

В работе [2] рекомендовано применение полиномиальных аппроксимаций закона Барри-Конвея (4) в виде:

(5)

Тогда при наличии полиномиальных аппроксимаций закона Барри-Конвея (4) общее уравнение нелинейной фильтрации флюида для больших скоростей будет представлено в виде [2]:

(6)

Далее в работе [2] предложен способ, по которому находятся параметры

Однако, как кажется, основная трудность заключается в правильном нахождении коэффициентов по данным гидрогазодинамических исследований.

В связи с этим предлагается следующая методика.

Для этого сначала получим некоторые необходимые формулы. Используя формулы (1) и (5), можно записать:

(7)

Учитывая, что в этой формуле , (8)

то получаем:

(9)

Интегрируя правую часть выражения от а левую часть от получаем:

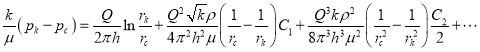(10)

Так как, 1 где, i =1, n то этими выражениями можно пренебречь. Разделив обе части выражения на и применяя формулы (8), получаем:

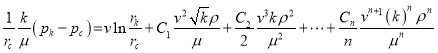
или 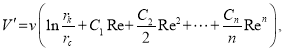(11)

где

Согласно методике коэффициенты и показатель степени n находятся, по данным гидрогазодинамических исследований скважин при установившихся режимах фильтрации. Индикаторные линии строятся в координатах так, как зная зависимость Q=Q (Δp) нетрудно построить и график функции . При этом могут иметь место три возможных случая.

1. не изменяется в зависимости от Re.

В этом случае мы имеем дело с линейным законом Дарси:

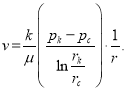
В указанных выше координатах полученная горизонтальная прямая отсекает от оси ординат отрезок, равный . По этому отрезку можно определить радиус дренирования скважины .

2. изменяется в зависимости от Re по линейному закону. По отрезку, отсекаемому на оси ординат и углу наклона полученной прямой, определяются соответственно

В этом случае мы имеем дело с законом Форхгеймера. Здесь В этом случае также можно определить радиус дренирования и коэффициент , при двучленном законе фильтрации,

3. изменяется в зависимости от Re не по линейному закону. И в этом случае индикаторные линии, построенные в указанных координатах, экстраполируются до оси ординат , и по отрезку, отсекаемому на ней, определяется После определения радиуса дренирования индикаторную линию следует перестраивать в координатах 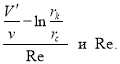Так как при этом из формулы (11) получается

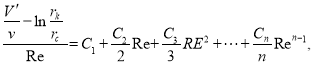(12)

то, средствами MS Exsel [7] находим коэффициенты Подставляя эти значения в (2) и (5), мы получим общий нелинейный закон фильтрации флюидов при больших градиентах давления. От этих формул легко можно перейти к формуле Барри-Конвея, однако думаю, что в этом нет необходимости, так как полиноминальная формула является самой удобной формой как для обработки по данным гидрогазодинамических исследований, так и для интегрирования.

Литература:

1. Басниев К. С. Нефтегазовая гидромеханика /К. С. Басниев, Н. М. Дмитриев, Г. Д. Розенберг. — Москва-Ижевск: Институт компьютерных исследований, 2005.
2. В. А. Толпаев, К. С. Ахмедов, С. А. Гоголева. Нелинейные законы фильтрации флюидов при больших скоростях потоков // Нефть и газ. — № 5. — 2015.
3. Barree R. D. Beyond beta factors: f complete model for Darcy, Forchheimer and trans-Forchheimer flow in porous media / Barree R. D., Conway M. W. // Paper SPE 89325 presented at the 2004 annual technical conference and exhibition, Houston, Texas 26–29 Sept 2004.
4. Barree R. D. Reply to Discussion of “Beyond Beta Factors: A Complete Model for Darcy, Forchheimer and Trans- Forchheimer Flow in Porous Media” / Barree R. D., Conway M. W. // — Journal of Petroleum Technology. –Aug. 2005. –Pp. 73–74.
5. Jambhekar V. A. Forchheimer Porous-media Flow Models-Numerical Investigation and Comparison with Experimental Data [Текст]: Master^,s Thesis. — Stuttgart, 2011. –85 p.
6. Куршин А. П. Закономерности изменения проницаемости пористых сред при фильтрационных течениях. /А. П. Куршин //Ученые записки ЦАГИ. — Том XXXIX. – 2008. –№ 1–2. — С.125–135.
7. Спиридонов О. В. Расширенные возможности Microsoft Excel 2003 / О. В. Спиридонов. – Центр дистанционных образовательных технологий МИЭМП, 2010.