В работе находится вид производных динамических структур кинематических деревьев тел (кинетического момента и количества движения). Данные структуры необходимы для решения динамических задач систем тел.

Ключевые слова: кинематические деревья, робототехника, кинематика деревьев тел, динамические структуры, кинетический момент, количество движения, тензорное исчисление.

Для практического решения задач динамики иногда требуется по заданному движению определить динамические структуры абсолютно твердых тел и их производные:

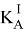1. — количество движения тела ,
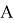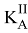2. — кинетический момент тела 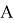относительно центра масс тела.

Пусть — множество тел системы. Структура связей между телами из множества эквивалентна неориентированному дереву [4] . Если то между телами имеется связь (сочленение) допускающее их относительное вращательное движение. — изоморфный для ориентированный граф:

.

Явный вид выражений динамических характеристик может быть достаточно громоздким. Для его нахождения введем следующие обозначения:

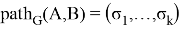1. — путь (последовательность ребер) из вершины 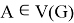в вершину ориентированного графа ,
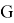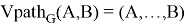2. — упорядоченная последовательность вершин, соответствующая пути ,
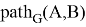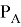3. — тензор ориентации тела ,
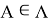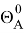4. — тензор инерции тела 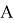в отсчетный момент времени,
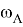5. — угловая скорость тела ,
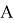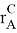6. — радиус-вектор центра масс тела A относительно неподвижной в данной инерциальной системе отсчета точки,
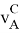7. — скорость центра масс тела A,
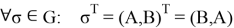8. — смена направления ребра графа.
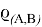9. — радиус-вектор неподвижной точки сочленения тел 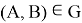в теле 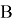относительно центра масс тела .

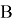Фиксируем тело . Предполагая, что тензоры ориентации звеньев кинематического дерева выражаются последовательными поворотами, положим:

,

.

Здесь — тензор относительной ориентации тела относительно тела . Таким образом записанное выражение является в совокупности неявным определением тензоров . Перепишем это определение в явной форме, учитывая, что тензор ориентации принадлежит собственно ортогональной подгруппе:

.(1)

Под понимается предыдущее по отношению к телу тело в дереве с корнем . Выражение (1) допустимо так как у каждого тела существует единственное предшествующее тело в дереве , кроме самого корня дерева. Однако, положим, что — единичный тензор. Тогда выражение допустимо для всех тел в кинематическом дереве.

Вычислим теперь кинематические характеристики тел, выраженные через характеристики относительных поворотов (далее — угловая скорость относительного вращения; — операция нахождения векторного инварианта тензора [1, 2]). Положим , для любого тела кинематического дерева, в соответствии с тензорной теоремой сложения угловых скоростей и теоремой о распределении скоростей в твердом теле [1,2,3], можем записать:

(2, 3)

При этом положение центра масс задается выражением:

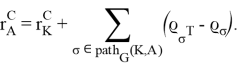
Раскрывая итеративно (2, 3) вдоль пути , получаем явные выражения:

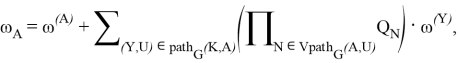
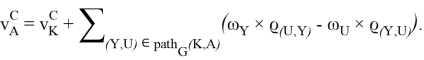
Продифференцируем полученные равенства:

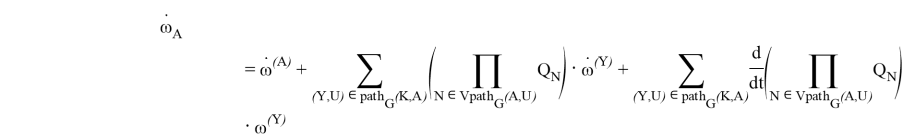
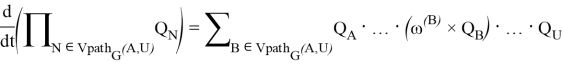
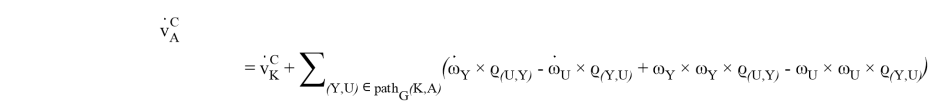
После вычисления кинематических характеристик стандартно вычисляются производные динамических структур и сами динамические характеристики тел системы [1] :

1. ,
2. 
3. ,
4. .

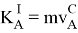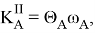
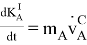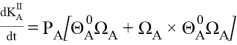— правый вектор угловой скорости.

Выполнив все изложенные шаги, придем к такому виду, что , оказываются однозначно параметризованны посредством , , . Таким образом с помощью задания данных тензорных параметров можно однозначно найти производную кинетического момента и количества движения всех твердых тел в системе. Для каждого конкретного механизма могут накладываться различные ограничения на тензоры относительных ориентаций тел. В этом случае количество независимых параметров оказывается меньше, чем количество указанных ранее параметров, в таком случае, по крайней мере локально, можно разрешить ограничения, наложенные на систему, и уменьшить количество переменных тензоров до числа независимых в локальной окрестности. Таким образом вид динамических структур и их производных найден.

Литература:

1. Жилин П. А. Динамика твердого тела. СПбГПУ, 2014.
2. Жилин П. А. Векторы и тензоры второго ранга в трехмерном пространстве. СПбГПУ, 2012.
3. Бабаджанянц Л. К., Пупышева Ю. Ю., Пупышев Ю. А. Классическая механика. Издательство Санкт-Петербургского Университета, 2011.
4. Оре О. Теория графов. Наука, 1980.