Изготовлена специальная установка, позволяющая поддерживать температуру до 3000 °C, необходимую для осуществления химических процессов в реакторе 1. Выполнено численно-аналитическое исследование температурного состояния многослойной цилиндрической установки с учётом лучистого теплообмена в газовой прослойке на всех режимах работы лабораторного стенда с помощью программы ANSYS Workbench.

Ключевые слова: численно-аналитический расчёт, сложный теплообмен, химический реактор, тепловой расчёт, многослойная цилиндрическая установка, лучистый теплообмен, программное обеспечение ANSYS Workbench.

Рассмотрим задачу стационарной теплопроводности применительно к трехслойному полому бесконечному цилиндру, у которого внутренний и наружный слои разделяются воздушной прослойкой (Рис.1). Температура внутренней стенки цилиндра известна и равна . Теплообмен на наружной поверхности цилиндра происходит при краевых условиях 3-го рода с заданными величинами коэффициента теплоотдачи и температуры среды . Требуется найти тепловой поток с единицы длины цилиндрической стенки, а также распределение температуры по толщине стенки.

Математическая постановка данной задачи будет:

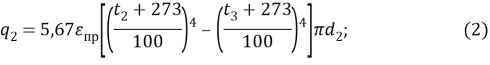
где − коэффициенты теплопроводности первого и третьего слоёв, ; − тепловой поток, переносимый посредством теплопроводности, Вт/м; − лучистый поток через воздушный слой, Вт/м; − тепловой поток, протекающий через наружный слой, Вт/м; − конвективный тепловой поток, Вт/м; − диаметры слоев трехслойного полого цилиндра (Рис.1).

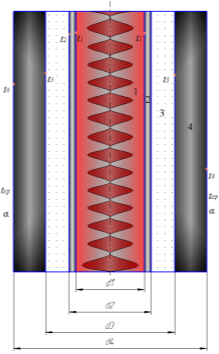
Рис.1 Схема лабораторной установки химического реактора: 1– химический реактор; 2 — первый слой (асбест); 3 — воздушная прослойка; 4 — слой стекловаты

Исходные данные задачи следующие (Рис.1):

.

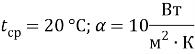Рассмотрим способ определения точного решения системы (1) — (4), позволяющий находить ее неизвестные, не используя графические методы. При стационарном режиме тепловые потоки в любом слое равны, т. е. . Поскольку число неизвестных ( равно четырём, то система (1) — (4) замкнута. Однако определение ее точного решения затрудняется нелинейностью уравнения (2). Для упрощения этой системы сведём соотношения (3) и (4) к одному алгебраическому уравнению. Выразим из (4) температуру и подставим полученное соотношение в (3).

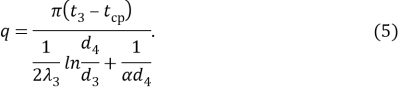
Из (5) следует, что температура оказалось исключенной из системы (2.4), (2), (5), решение которой необходимо теперь получить. Для дальнейшего упрощения системы (1), (2), (5) выразим температуру из уравнения (1), а − из уравнения (5) и подставим полученные выражения в соотношение (2). Откуда для теплового потока будем иметь степенное уравнение вида:

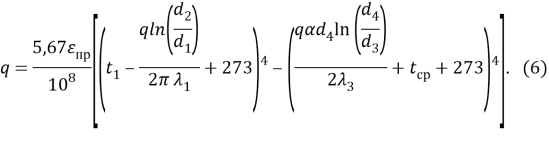
Соотношение (6) представляет алгебраическое уравнение 4 — й степени для искомого теплового потока . Это уравнение имеет четыре корня, три из которых не имеют физического смысла, два комплексных и один отрицательный. Следовательно, из решения уравнения (6) получаем один действительный корень, представляющий определяемый тепловой поток. Расчёты теплового потока по уравнению (6) для разных значений температуры () внутренней поверхности приведены в таблице 1.

По найденному тепловому потоку, по формулам (1), (3), (4), были найдены температуры , , , которые также приведены в табл. 1.

Таблица 1

Найдём расход охлаждающего воздуха Gвозд для всех режимов работы лабораторной установки:

(7)

где - средняя теплоёмкость воздуха на каждом режиме;

среднеарифметическая температура между и воздуха в прослойке 3 (Рис.1);

=20°С — температура наружного воздуха.

Зная расход охлаждающего воздуха, определим скорость его перемещения по формуле (8):

где 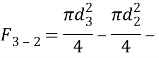площадь поверхности воздушной прослойки и равна:

Полученные результаты расхода охлаждающего воздуха и необходимой скорости охлаждения приведены в таблице 2.

Таблица 2

Определим количество теплоты, которое необходимо отвести от каждого изоляционного слоя для того, чтобы охладить его до 50 °С:

где ,массы изоляционных слоёв минеральной ваты и асбеста соответственно;

среднеарифметическая температура между и воздуха в прослойке 4 (Рис.1)

среднеарифметическая температура между и воздуха в прослойке 2 (Рис.1)

теплоёмкость изоляционных слоёв минеральной ваты и асбеста равны 920 Дж/(кг·°С) и1050 Дж/(кг·°С) соответственно;

где плотность изоляционного слоя,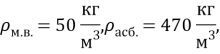

объём изолирующего слоя, определяющийся по формуле (9):

(9)

где высота изоляционного слоя, h=1,2 м;

площадь изоляционного слоя.

Найдём объёмы изолирующих слоёв:

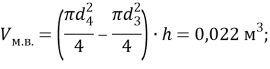
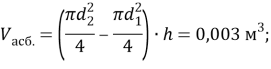
Определим время охлаждения каждого изоляционного слоя для последнего режима:

Найдём коэффициент теплоотдачи

где коэффициент теплопроводности воздуха при

толщина изоляционного слоя, являющая определяющим размером.

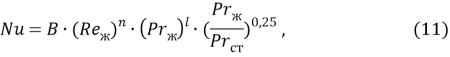
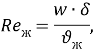
где кинематическая вязкость воздуха,

определяющий размер, толщина

необходимая скорость охлаждения, м/с;

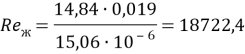
Полученные значения поставим в уравнение (11) и найдём критериальный коэффициент , для каждого изоляционного слоя при последнем режиме работы:

Полученные значения коэффициента подставим в уравнение (10) и найдём коэффициент теплоотдачи воздуха ( от каждого изоляционного слоя при последнем режиме работы:

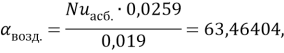
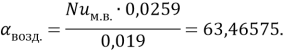
Исходя из полученных значений, решим задачу нестационарного охлаждения лабораторной установки в модуле Transient Thermal программы ANSYS Workbench. Для этой цели, используя результаты аналитического решения задачи (1) — (4), приведенные в табл. 1, было задано начальное температурное распределение внутри установки (рис. 2)

Рис. 2. Начальное распределение температуры при q=1485 Вт/ и схема разбиения на конечные элементы

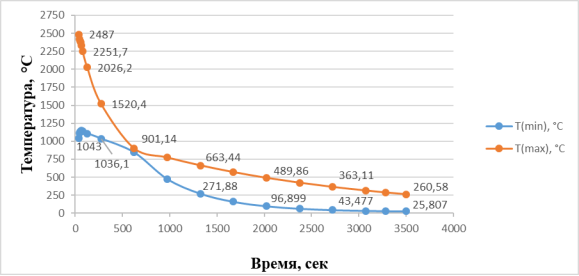
Рис. 3. Графики изменения максимальных и минимальных температур в лабораторной установке от времени

Заключение

1. Найдены скорости движения охлаждающего воздуха в зазоре 2 (рис.1) лабораторной установки, подающегося вентилятором для поддержания температуры на поверхности стенда не более 50 °С для всех режимов работы на основе численно-аналитического расчёта;
2. Определено время охлаждения химического реактора атмосферным воздухом, подаваемым вентилятором, для рабочей температуры (3000 °С) электрической спирали лабораторного стенда.

Литература:

1. Кудинов И. В., Абишева Л.С, Бранфилева А. Н. Вестник СГАСУ. Градостроительство и архитектура: научно-технический журнал / СГАСУ. — Самара, 2014. — Вып. № 3(16). — 112 с.

2. Кудинов, И. В. Графоаналитический метод расчета потерь теплоты через многослойные стенки при наличии лучистого теплообмена между отдельными слоями [Текст] / И. В. Кудинов // Межвузовский сборник научных трудов “Повышение энергоэффективности зданий и сооружений”. Вып. 6 / СГАСУ. — Самара, 2011. − С. 74–80.

3. Михеев, М. А. Основы теплопередачи [Текст] / М. А. Михеев, И. М. Михеева. − М.: Энергия, 1997. − 344 с.

4. Исаченко, В. П. Теплопередача [Текст] / В. П. Исаченко, В. А. Осипова, А. С. Сукомел. − М.: Энергия, 1969. − 440 с.