Интегральная оценка финансового состояния АО «Янтарьэнерго»

Левченко Яна Александровна, магистрант

«Калининградский государственный технический университет»

В статье рассматриваются особенности интегральной оценки финансового состояния бизнеса, приводятся примеры моделей, позволяющих получить интегральный показатель, оценивается вероятность банкротства объекта оценки.

Ключевые слова: Интегральная оценка бизнеса; финансовое состояние предприятия; динамическая система; функция принадлежности; нечеткое множество.

Для того, чтобы проанализировать финансовое состояние компании, необходимо вычислить и исследовать большое количество показателей. При этом возникают трудности, заключающиеся в получении одного интегрального показателя, характеризующего состояние компании в целом среди множества локальных показателей. На сегодняшний день существует ряд моделей, позволяющих получить интегральный коэффициент для оценки финансового состояния предприятия и вероятности риска банкротства предприятия. Самой известной из них является Z-модель Альтмана, однако она была разработана в США еще в 1950−1970 гг. и не может учитывать особенности современной экономической ситуации в России.

Сложные динамические экономические системы обычно характеризуются неполнотой информации, неустойчивостью, эволюционными изменениями и пр. Во многих задачах информация поступает от эксперта. Эта информация обычно характеризуется неточностью, поступает не в виде количественных, а в виде лингвистических переменных. Такой язык является более понятным для людей и позволяет свободно обмениваться информацией. Поэтому нечисловые статистические методы анализа целесообразно использовать в экономических исследованиях [4, 5].

При оценке деятельности предприятия часто приходится иметь дело с нечисловыми данными (качественными характеристиками), например, с такими понятиями, как «низкий» — «высокий», «плохой» — «хороший». Многие финансовые показатели не имеют четкого нормирования и сильно зависят от сферы деятельности предприятия, в таких случаях часто прибегают к экспертным оценкам. Классические модели оценки финансового состояния не могут работать с такими данными, поэтому в этом случае можно воспользоваться аппаратом нечетких множеств.

Понятие «нечеткие множества» было введено Л. Заде в 1965 г. [6]. Дальнейшее развитие указанная тема получила в работе А. Кофмана [7]. В области применения аппарата нечетких множеств для анализа деятельности предприятия наиболее известны работы А.О. Недосекина [2]. Этот аппарат может применяться не только в области финансового анализа, но и для решения других задач, например, для оценки качества образования с точки зрения потребителей образовательных услуг [1].

В данном исследовании анализируется деятельность АО «Янтарьэнерго», оценка произведена для трехлетнего периода с 2014 по 2016 г.

Пусть D(Xi) — область определения произвольного отдельного финансового или управленческого показателя Xi, несчетное множество точек оси действительных чисел. Зададим лингвистическую переменную Bi «Уровень показателя Xi», имеющую 5 значений: Bi1 – Bi5, соответствующих нечетким подмножествам множества D(Xi) «очень низкий уровень показателя», «низкий уровень показателя», «средний уровень показателя», «высокий уровень показателя», «очень высокий уровень показателя». Каждому из подмножеств Bi1 – Bi5 соответствуют свои функции принадлежности (Xi) , где i = 1, ..., 5. В результате применения методики из локальных показателей получим комплексный показатель V.

Введем лингвистическую переменную А «Финансовое состояние предприятия», которая имеет 5 значений: А₁ - А₅ , соответствующих нечетким подмножествам «состояние предельного неблагополучия», «состояние неблагополучия», «финансовое состояние среднего качества», «состояние относительного благополучия», «состояние предельного благополучия» [9]. Каждому из подмножеств A1 – A5 соответствуют своим функциям принадлежности  i (V ) , где i = 1, ..., 5. Причем чем выше V, тем лучше его финансовое состояние.

Функции принадлежности  i (V) соответствует нечеткое трапециевидное число (Т - число) ____ где _, _ — абсциссы нижнего основания, а __абсциссы верхнего основания трапеции.

Для анализа финансовой устойчивости предприятия используются следующие показатели: коэффициент автономии (X1), коэффициент обеспеченности оборотных активов собственными средствами (X2), коэффициенты промежуточной и абсолютной ликвидности (X3, X4), оборачиваемость всех активов в годовом исчислении (X5) и рентабельность всего капитала (X6) (табл.1)

Таблица 1

Значения финансовых показателей в АО «Янтарьэнерго» 2014 – 2016 гг.

Коэффициенты i могут принимать значения ±1 в зависимости от того, приводит ли рост показателя Хi к прямому или обратному влиянию на комплексный показатель V. Будем считать, что все показатели обладают одинаковой значимостью, т.е. имеют равные веса рi = 1/6 0,167. Посмотрим классификацию значения V как критерий разбиения множества его значений на нечеткие подмножества Ai, i = 1,…,5 (табл. 2) [6].

Таблица 2

Классификация значений комплексного показателя V

В ячейках табл. 3 уже стоят трапециевидные числа, характеризующие соответствующие функции принадлежности.

Таблица 3

Классификация отдельных финансовых показателей

Таблица 4

Классификация уровня значений коэффициента автономии X1

Функции принадлежности также можно представить в аналитическом виде аналогично классификации степени риска банкротства.

На основе построенных функций принадлежности и значений финансовых показателей осуществляется расчет значений функций принадлежности λ_t (x_i ^{2014,2015,2016}) для t = B₁, В₂, …, В₅ и распознавание уровня показателей для нашего примера (табл. 5).

Таблица 5

Распознавание уровня значений показателей Хi

Таблица 6

Значения промежуточных коэффициентов Yt

Рассчитаем промежуточный коэффициент Yt, t = B1, B2, ..., B5 по следующей формуле [2]:

где t указывает на соответствующий элемент из терм-множества лингвистической переменной B «Уровень значений показателя Xi», причем i определяется из табл. 3.1, а t(xi) находится в табл. 5. Для примера приведем расчет коэффициента Y_B1 2014:

Y_B1 2014 = (1 0,167 1  1 0,167 1) / (1 0,167  1 0,167  1 0,167  1 0,167  1 0,167  1 0,167) = 0,334.

Остальные коэффициенты рассчитываются аналогично (табл. 6). Далее рассчитаем комплексный показатель V по следующей формуле:

V = (v1, v2 , v3 , v4) = YВi  βAi (1),

где Вi = 1,…,5, знак «» выражает операцию умножения действительного числа на нечеткое число, значения Yi вычисляются по формуле (1), Т-числа {} описывают функции принадлежности лингвистической переменной A «Финансовое состояние предприятия».

Получаем следующие результаты:

V2014  (0, 40416;0, 48736;0, 63235;0, 72557);

V2015  (0, 23714;0,30394;0, 42919;0,51269);

V2016  (0,19806;0, 25885;0, 46726;0, 47060).

Переход от нечеткого числа V к действительному виду (дефаззификация), пригодному для использования лица, принимающего решение, можно осуществить методом среднего максимума:

V = ( v2 + v3) / 2

Пользуясь этим методом, получаем следующие результаты:

V₂₀₁₄ = 0,55985;

V₂₀₁₅ = 0,36656;

V₂₀₁₆ = 0,36305.

Другим методом дефаззификации является метод центра тяжести [6]:

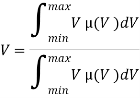
где  — переменная, соответствующая выходной лингвистической переменной и принимающая значения от  = min до  = max;

min и max — левая и правая точки интервала носителя нечеткого множества;

(V) — функция принадлежности нечеткого множества.

С помощью графических представлений интегральных показателей можно записать функции принадлежности показателей V в аналитическом виде. Для примера покажем функции принадлежности для 2014 г. (в табл. 7)

Таблица 7

Функция принадлежности показателя V2014

Пользуясь данным методом, получаем следующие результаты:

V₂₀₁₄ = 0,56298;

V₂₀₁₅ = 0,37126;

V₂₀₁₆ = 0,34804.

Результаты, полученные разными методами, в целом друг другу не противоречат.

Проведем распознавание финансового состояния предприятия на основе результатов, полученных с помощью двух разных методов дефаззификации. Сделать это можно с помощью сформированной ранее табл. 2. С определенной степенью уверенности делаем вывод о степени финансовой устойчивости предприятия (табл. 8).

Таблица 8

Распознавание уровня финансового состояния АО «Янтарьэнерго»

Заметим, что в 2014 г. интервалы значений попадания показателя V разные. Это демонстрирует различие результатов применения методов: методы дают значения показателя V, различающиеся во втором знаке, и согласно классификации, приведенной в табл. 3.2, метод среднего максимума дает состояние «среднего качества», хотя и с совсем небольшой степенью оценочной уверенности (13%).

Финансовое состояние предприятия «Янтарьэнерго» по итогам 2014 г. признается средним с большим уровнем соответствия в обоих методах (0,90145 и 0,8732 соответственно) и с меньшим уровнем соответствия относительно благополучным (0,09855 и 0,1268). Степень риска возникновения на предприятии банкротства обратно зависима от его финансового состояния, поэтому степень риска банкротства в 2014 г. признается средней (со степенью уверенности 0,90145 и 0,8732) и низкой (со степенью уверенности 0,09855 и 0,1268).

По итогам 2015 г. финансовое состояние предприятия признается средним с уровнем соответствия 0,16565 и 0,2126 и неблагополучным с уровнем соответствия 0,83435 и 0,7874. В 2013 г. степень риска банкротства признается средней (со степенью уверенности 0,16565 и 0,2126) и высокой (со степенью уверенности 0,83435 и 0,7874).

В 2016 г. финансовое состояние предприятия на основании метода среднего максимума признается средним с уровнем соответствия 0,13058 и неблагополучным с уровнем соответствия 0,86942. На основании метода центра тяжести финансовое состояние предприятия признается неблагоприятным с уровнем соответствия 1. Степень риска возникновения на предприятии банкротства в 2016 г. с большей степенью уверенности является высокой.

Таким образом, было исследовано финансовое состояние предприятия АО «Янтарьэнерго» в 2014 – 2016 гг. с помощью аппарата нечетких множеств. Для целей анализа были рассчитаны 6 локальных финансовых показателей, при анализе по отдельности одни из них говорили об устойчивом финансовом положении предприятия, а другие — о высокой степени риска банкротства. С помощью аппарата нечетких множеств был получен интегральный показатель степени риска банкротства, на основе которого возможно делать вывод о финансовой устойчивости предприятия. Таким образом, с помощью аппарата нечетких множеств довольно удобно анализировать финансовое состояние предприятия.

С помощью этой методики можно анализировать финансовое состояние различных предприятий, учитывая особенности их функционирования. В отличие от традиционных методик применение нечетких множеств позволяет проводить более точную оценку хозяйственной деятельности. Особенно важно это в современных российских условиях, когда для выхода из кризиса необходимо развитие собственного конкурентоспособного устойчивого производства.

Литература:

1. Гридин, В. С. Оценка стоимости предприятии как элемент эффективного управления/ В. С. Гридин, М. Ф. Тестина // Материалы пятой межрегиональной научной конференции «Студенческая наука – экономике России». – Ставрополь, 2015.
2. Есипов, В. Е. Оценка бизнеса: учебное пособие / В. Е. Есипов, Г. А. Маховикова, В. В. Терехов. – 2-е изд. – СПб.: Питер, 2016. – 464 с.
3. Зимин, А. И. Оценка имущества: вопросы и ответы / А. И. Зимин. – М.: Юриспруденция, 2016. – 240 с.
4. Ибрагимов, Р. Г. Управление по стоимости как система менеджмента / Р. Г. Ибрагимов// Менеджмент в России и за рубежом. – 2014.- № 6.
5. Коупленд, Т. Стоимость компаний: оценка и управление / Т. Коупленд, Т. Колер, Дж. Мурин; пер с англ. Н. Н. Барышниковой. – М.: Олимп-Бизнес, 2015. – 576 с.
6. Кузнецов, С. Оценка бизнеса / С. Кузнецов // Аудит и налогообложение. – 2015. -№ 6. – С. 24-26.
7. Минаева, О. А. Инструменты измерения и методы управления экономическим потенциалом промышленной организации: канд. экон. наук: 08.00.05 / О. А. Минаева. - Волгоград, 2016. – 247 с.