Таблица 1
Представление материала в виде списка
|
|
№Д.Е. |
Время на изучение |
Коэффициент весаД.Е. |
Количество входныхД.Е. |
|
Д.Е. вх. |
1 |
0.3 |
1 |
0 |
|
2 |
1 |
1 |
0 | |
|
3 |
1.1 |
11 |
0 | |
|
4 |
0.2 |
1 |
1 | |
|
5 |
0.3 |
1 |
1 | |
|
6 |
0.1 |
1 |
1 | |
|
7 |
0.5 |
1 |
1 | |
|
8 |
0.6 |
2 |
1 | |
|
9 |
0.8 |
2 |
1 | |
|
10 |
0.9 |
1 |
1 | |
|
11 |
0.1 |
1 |
6 | |
|
12 |
0.2 |
1 |
4 | |
|
13 |
1 |
2 |
1 | |
|
14 |
1.5 |
1 |
4 | |
|
15 |
0.6 |
1 |
0 | |
|
16 |
0.6 |
1 |
2 | |
|
17 |
0.8 |
1 |
1 | |
|
19 |
1 |
1 |
1 | |
|
20 |
1 |
1 |
2 | |
|
Д.Е. вых. |
21 |
6,6 |
0 |
4 |
Воспользуемся Таблицей 1, и представим наглядно дидактические единицы вместе со временем, которое необходимо для их освоения. Зная время на освоение каждой дидактической единицы, можно рассчитать время для каждой схемы не освоенных дидактических единиц, которое потребуется для их повторного освоения.
В каждой из представленных вариаций (см. Рис. 1, Рис. 2) можно найти дополнительное время, которое необходимо будет затратить на освоение дидактических единиц. В первом случае 1,4ч во втором 1,2ч. В первом случае итоговая сумма на освоение всех дидактических единиц увеличится с 6,6ч до 8ч, во втором же случае до 7,8ч.
Каждая вариация, является отражением незнания по каждому конкретному студенту, что дает возможность статистически предположить, сколько в среднем может понадобиться дополнительного времени на освоение дидактических единиц, путем расчета средней. В долгосрочной перспективе, если средняя будет иметь устоявшийся вид, то можно распределить ее время по дидактическим единицам, приведя тем самым общее время к более реалистичному виду.
Если рассмотреть всю схему взаимосвязанных дидактических единиц, то она будет представлена в виде последовательного графа, где одна дидактическая единица может быть изучена только после изучения всех предыдущих дидактических единиц, что говорит о их жесткой взаимосвязи.
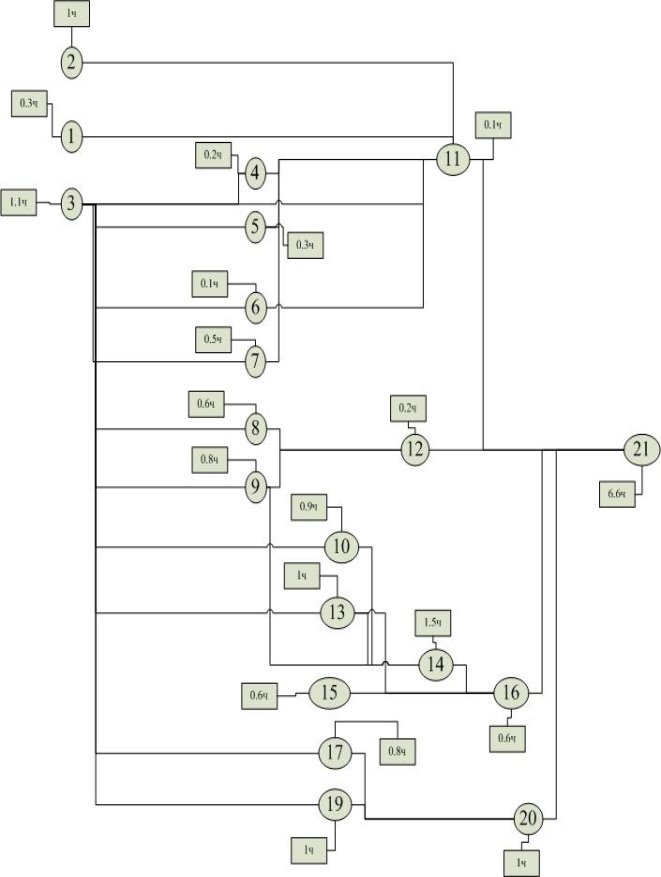
Рис. 1. Схема дидактических единиц со временем изучения каждой дидактической единицы
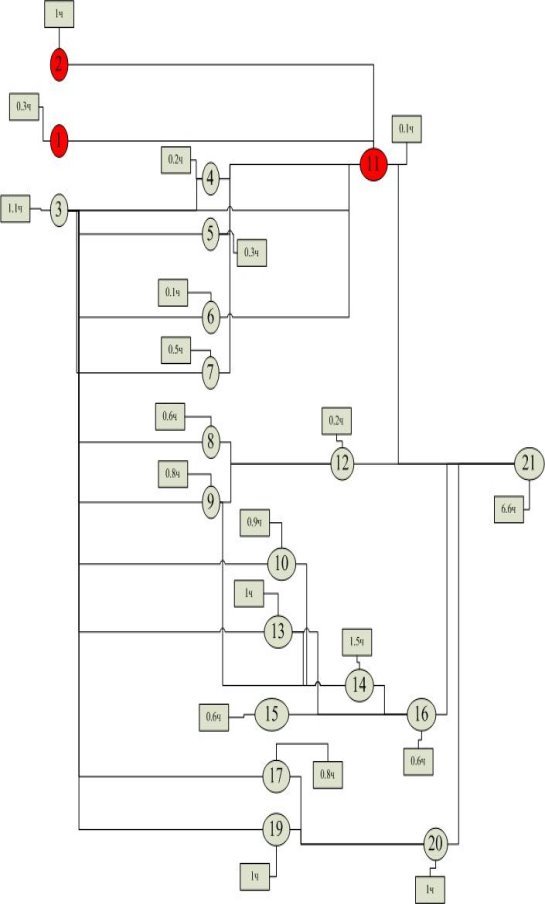
Рис. 2. Первый пример не освоенных дидактических единиц с указанием времени
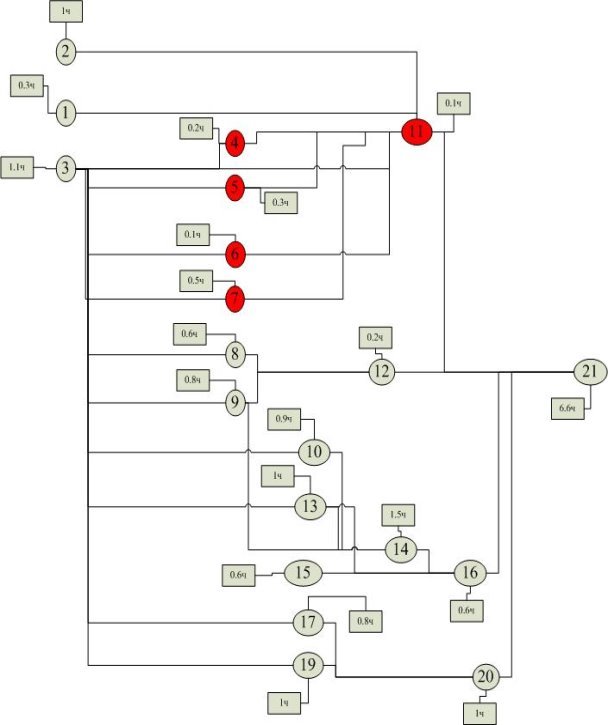
Рис. 3. Вторая вариация не освоенных дидактических единиц
Такая организация дидактических единиц не позволяет провести методы оптимизации изучения итоговой дидактической единицы, как в случае если бы имелась возможность изучения дидактической единицы, зная не все входящие в нее единицы, что позволило бы прибегнуть к методу динамического программирования Беллмана, и найти наименьшее время на изучение итоговой дидактической единицы. Если в графе дидактических единиц и имеется подобная организация, то она будет носить вырожденный характер.
Однако, если предположить, что дидактическая единица для своего освоения не требует от студента сто процентного результата, а достаточно знать ее в какой-либо степени, т. е. можно предположить, что дидактическая единица имеет некоторую степень знания. Чем выше данная степень, тем больший процент знаний необходим, чтобы считать освоенной данную дидактическую единицу. Например, если рассматривать таблицу умножения, то можно с полной уверенностью говорит о том, что для ее освоения необходимо пройти тест на сто процентов. Но, если взять понятие «число», то можно говорить о, том, что знание его определения не требуется в сто процентном виде. Большинство людей на Земле, не сможет дать его точное определение, но при этом они точно представляют себе, что подразумевает и означает данное понятие. Таким образом, на примере данных понятий, можно с уверенностью сказать, что они обладают разными степенями знания, а значит, что для понятий, в которые входит таблица умножения, может существовать только один путь освоения, если они состоят только из подобных дидактических единиц. А для понятий, в которые входит дидактическая единица «число», может существовать несколько путей достижения, тогда можно говорить о нахождении наиболее быстрого пути освоения данных понятий.
Литература:
- В. Е. Пешкова. Педагогика Часть 4. Теория обучения (дидактика) учеб. пособие для студ. вузов. — 2010: Майкоп, 2010. — 149 с.;
- В. В. Конев Векторная. Алгебра: учеб. пособие для студ. вузов. — 2008г: Томский политехнический университет, 2008г. — 34 с.;
- В. Е. Пешкова. Педагогика Часть 6. Педагогическая информатика (дидактика) учеб. пособие для студ. вузов. — 2010: Майкоп, 2010. — 151 с.;
- Голованова Ю. В. Модульность в образовании: методики, сущность, технологии // Молодой ученый. — 2013. — № 12. — С. 422–437;
- М. В. Кондурар. Понятие компетенция и компетентность в образовании // 2011. — 2011. — № 2(5). — С. 212–220.
- Федеральный закон от 29 декабря 2012 г. № 273-ФЗ (ред. от 03.07.2016) «Об образовании в Российской Федерации» (с изм. и доп., вступ. в силу с 15.07.2016) // КонсультантПлюс. URL: http://www.consultant.ru/document/cons_doc_LAW_140174/ (дата обращения: 9.10.2016).

