Из-за быстрого развития Интернета и эволюции цифровых технологий, доступность цифрового контента очень возросла. Технология водяных знаков, которая позволяет незаметное встраивание информации в оригинальные данные, широко применяется для защиты авторских прав и идентификации владельца. Также она может быть использована для отслеживания  мультимедиа продуктов, которые нелегально распространяются.

Искусственные нейронные сети (ИНН) нашли широкое применение в системах цифровых водяных знаков из-за своей способности к запоминанию и классификации образов.

Способность искусственных нейронных сетей обучаться является их наиболее интригующим свойством. Подобно биологическим системам, которые они моделируют, эти нейронные сети сами моделируют себя в результате попыток достичь лучшей модели поведения.

Используя критерий линейной разделимости, можно решить, способна ли однослойная нейронная сеть реализовывать требуемую функцию. Даже в том случае, когда ответ положительный, это принесет мало пользы, если у нас нет способа найти нужные значения для весов и порогов. Чтобы сеть представляла практическую ценность, нужен систематический метод (алгоритм) для вычисления этих значений. Розенблатт [1] сделал это в своем алгоритме обучения персептрона вместе с доказательством того, что персептрон может быть обучен всему, что он может реализовывать.

Обучение может быть с учителем или без него. Для обучения с учителем нужен «внешний» учитель, который оценивал бы поведение системы и управлял ее последующими модификациями. При обучении без учителя, рассматриваемого в последующих главах, сеть путем самоорганизации делает требуемые изменения. Обучение персептрона является обучением с учителем.

Алгоритм обучения персептрона может быть реализован на цифровом компьютере или другом электронном устройстве, и сеть становится в определенном смысле самоподстраивающейся. По этой причине процедуру подстройки весов обычно называют «обучением» и говорят, что сеть «обучается». Доказательство Розенблатта стало основной вехой и дало мощный импульс исследованиям в этой области. Сегодня в той или иной форме элементы алгоритма обучения персептрона встречаются во многих сетевых парадигмах.

Алгоритм обучения персептрона

Персептрон обучают, подавая множество образов по одному на его вход и подстраивая веса до тех пор, пока для всех образов не будет достигнут требуемый выход. Допустим, что входные образы нанесены на демонстрационные карты. Каждая карта разбита на квадраты и от каждого квадрата на персептрон подается вход. Если в квадрате имеется линия, то от него подается единица, в противном случае – ноль. Множество квадратов на карте задает, таким образом, множество нулей и единиц, которое и подается на входы персептрона. Цель состоит в том, чтобы научить персептрон включать индикатор при подаче на него множества входов, задающих нечетное число, и не включать в случае четного.

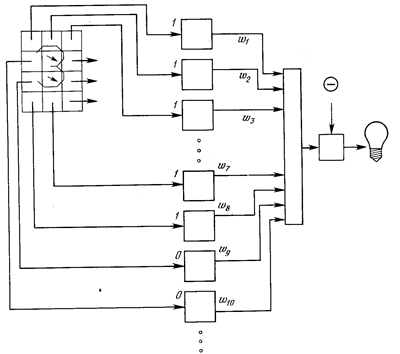
Рис. 1. Персептронная система распознавания изображений.

На рис. 1 показана такая персептронная конфигурация. Допустим, что вектор Х является образом распознаваемой демонстрационной карты. Каждая компонента (квадрат) Х – (x₁, x₂, …, x_n) – умножается на соответствующую компоненту вектора весов W – (w₁, w₂, ..., w_n). Эти произведения суммируются. Если сумма превышает порог Θ, то выход нейрона Y равен единице (индикатор зажигается), в противном случае он – ноль. Эта операция компактно записывается в векторной форме как Y = XW, а после нее следует пороговая операция.

Для обучения сети образ Х подается на вход и вычисляется выход Y. Если Y правилен, то ничего не меняется. Однако если выход неправилен, то веса, присоединенные к входам, усиливающим ошибочный результат, модифицируются, чтобы уменьшить ошибку.

Чтобы увидеть, как это осуществляется, допустим, что демонстрационная карта с цифрой 3 подана на вход и выход Y равен 1 (показывая нечетность). Так как это правильный ответ, то веса не изменяются. Если, однако, на вход подается карта с номером 4 и выход Y равен единице (нечетный), то веса, присоединенные к единичным входам, должны быть уменьшены, так как они стремятся дать неверный результат. Аналогично, если карта с номером 3 дает нулевой выход, то веса, присоединенные к единичным входам, должны быть увеличены, чтобы скорректировать ошибку.

Этот метод обучения может быть подытожен следующим образом:

1.      Подать входной образ и вычислить Y.

2.      а)   Если выход правильный, то перейти на шаг 1;

б)   Если выход неправильный и равен нулю, то добавить все входы к соответствующим им весам; или

        в)  Если выход неправильный и равен единице, то вычесть каждый вход из соответствующего ему веса.

3. Перейти на шаг 1.

За конечное число шагов сеть научится разделять карты на четные и нечетные при условии, что множество цифр линейно разделимо. Это значит, что для всех нечетных карт выход будет больше порога, а для всех четных – меньше. Отметим, что это обучение глобально, т. е. сеть обучается на всем множестве карт.

Важное обобщение алгоритма обучения персептрона, называемое дельта-правилом, переносит этот метод на непрерывные входы и выходы. Чтобы понять, как оно было получено, шаг 2 алгоритма обучения персептрона может быть сформулирован в обобщенной форме с помощью введения величины δ, которая равна разности между требуемым или целевым выходом T и реальным выходом Y

                                    δ = (T - Y).                                                                   (1)

Случай, когда δ=0, соответствует шагу 2а, когда выход правилен и в сети ничего не изменяется. Шаг 2б соответствует случаю δ > 0, а шаг 2в случаю δ < 0.

В любом из этих случаев персептронный алгоритм обучения сохраняется, если δ умножается на величину каждого входа х_i и это произведение добавляется к соответствующему весу. С целью обобщения вводится коэффициент «скорости обучения» η, который умножается на δх_i, что позволяет управлять средней величиной изменения весов.

В алгебраической форме записи

                                    Δ_i = ηδx_i,                                                                      (2)

                                    w(n+1) = w(n) + Δ_i,                                                      (3)

где Δ_i – коррекция, связанная с i-м входом х_i; w_i(n+1) – значение веса i после коррекции; w_i{n) -значение веса i до коррекции.

Дельта-правило модифицирует веса в соответствии с требуемым и действительным значениями выхода каждой полярности как для непрерывных, так и для бинарных входов и выходов. Эти свойства открыли множество новых приложений [2].

Примером применения ИНН в системах водяных знаков является запоминание отношений между оригинальным изображением после вейвлет-преобразования и подписанным [3]. Рис.2 показывает архитектуру НН, которая имеет три слоя: входной слой с 16 нейронами, скрытый слой с 12 нейронами и выходной слой с единственным нейроном. НН есть т.н. 16-12-1 многослойный перцептрон (МСП). Обучающий алгоритм обратного распространения применяется для тренировки НН, с помощью коррекции весов. Веса подстраиваются, чтобы уменьшить ошибки между входами и их соответствующими выходами. Физический выход НН представляется в виде .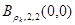

Множество тренировочных моделей 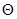 можно собрать и выразить в форме

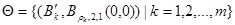      (4)

Где вектор 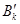 означает входную модель 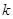-той тренировочной модели в 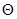, и представляется в виде:

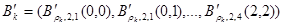        (5)

Кроме того, 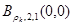 есть желаемый выход 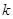-той тренировочной модели.

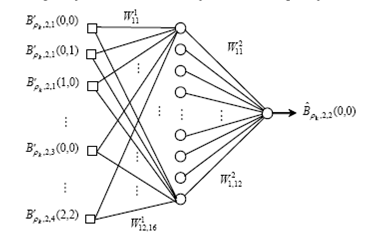
Рис.2. Архитектура НН, используемой в предлагаемой технике.

1.                 Розенблатт Ф. Принципы нейродинамики. – М: Мир. – 1965.

2.                 Минский М. Л., Пейперт С. Персептроны. – М: Мир. – 1971.

3.                 S. Haykin, Neural Networks: A Comprehensive Foundation, 2th ed., New York, Macmillan  College Publishing Company, 1999.