В статье рассмотрены особенности дискретизации нормального сечения железобетонного элемента с неоднородными свойствами бетона по толщине при реализации расчета по деформационной модели. Приведены указания по трансформации выражений, определяющих жесткостные характеристики сечения при переменных деформативных параметрах бетона. Предложен оптимальный подход к дискретизации сечения, обеспечивающий необходимое количество участков разбиения в условиях приобретенной при изготовлении и эксплуатации неоднородности свойств бетона.

Ключевые слова: железобетонный элемент, бетон, деформационная модель, жесткостные характеристики, неоднородные свойства, дискретизация, сечение

Железобетон является композиционным материалом, которому характерно упругопластическое деформирование под нагрузкой. Поведение железобетона при нагружении определяется свойствами составляющих его материалов и особенностями их совместной работы. Усадка, ползучесть и анизотропность бетона, наличие допускаемых трещин в конструкциях при эксплуатации, возможные нарушения сцепления стальной арматуры с бетоном определяют уникальные особенности деформирования железобетона, зависимости теоретического описания которого базируются на эмпирическом знании. В основу теории сопротивления железобетона заложены известные закономерности деформирования бетона и стальной арматуры под нагрузкой, которые нередко представляют в виде диаграмм состояния материалов. Длительное время нелинейные свойства бетона учитывались в нормах на проектирование упрощенно через расчетные коэффициенты, без явной зависимости от градиента деформаций по нормального сечению и уровня напряжений. Впервые физико-механические свойства бетона и арматуры в отечественных нормах проектирования были представлены в виде диаграмм состояния в своде правил СП 52–101–2003 «Бетонные и железобетонные конструкции без предварительного напряжения арматуры». А введенная в нормативные документы нелинейная деформационная модель расчета железобетонных элементов позволила производить учет диаграмм состояния бетона и арматуры в явном виде. В редакции свода правил СП 63.13330.2012 «Бетонные и железобетонные конструкции. Основные положения» данный подход к расчету железобетонных элементов сохранен.

Суть деформационной модели заключается в дискретизации сечения, нормального к продольной оси элемента. Площадь сечения разбивается на отдельные участки, как правило, малых размеров по сравнению с исходными габаритами. В общем случае при разделении элементарные участки бетонной части сечения задают, как правило, прямоугольной или квадратной формы площадью A_bi. В частном случае, при действии изгибающего момента в одной из плоскостей симметрии сечения, рациональным является его разделение на элементарные полоски (рис. 1, а), что сокращает трудоемкость дискретизации сечения и уменьшает число слагаемых в разрешающих уравнениях. По этому же принципу в армировании выделяются отдельные стержни с индивидуальной площадью или группы стержней с суммарной площадью A_sj.

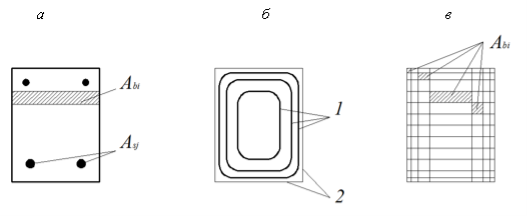
Рис. 1. Сечение, нормальное к продольной оси элемента: а — при дискретизации на полоски с однородными свойствами бетона; б — с отображением изолиниями 1 характера распределения неоднородных физико-механических свойств в пределах границ сечения 2; в — при разбиении с неоднородными свойствами бетона

В основу деформационной модели расчета железобетонных конструкций по сечению, нормальному к продольной оси элемента, положены следующие физические зависимости (обозначения в формулах (1)-(9) приняты в соответствии с СП 63.13330.2012):

(1)

(2)

(3)

Жесткостные характеристики сечения определяются по формулам:

(4)

(5)

(6)

(7)

(8)

(9)

Исходя из приведенных выражений (1)-(9) видно, что общие деформации железобетонного элемента , , при внутренних усилиях М_х, М_у, N определяются жесткостными параметрами, величина которых, в свою очередь, зависит от площади сечения и его формы (заложено в А_bi и в координатах z_bxi, z_byi соответственно), площади и положения арматуры (A_sj и z_sxj, z_syj), деформативных свойств бетона и арматуры (Е_b и E_s соответственно) и степенью проявления неупругих деформаций в материалах в пределах отдельных элементарных участков на уровне их центров тяжестей (ν_bi, ν_sj).

Количество элементарных участков бетона i и арматуры j определяется проектировщиком или заранее закладывается в вычислительные комплексы САПР при программировании расчета. Разбиение сечения с высокой степенью дискретизации, как правило, рационально при значительных градиентах деформаций по бетону сечения, а также при существенной неоднородности физико-механических характеристик бетона. Исходные зависимости (4)-(9) предусматривают постоянные по сечению и неизменные во времени деформативные характеристики бетона, определяемые начальным модулем упругости Е_b и заданной зависимостью «напряжения-деформации». В действительности физико-механические показатели бетона изменяются во времени и могут характеризоваться увеличением или уменьшением значений показателей, определяющих жесткостные параметры элемента по сечению, нормальному к продольной оси элемента. При благоприятных условиях твердения, набора прочности и эксплуатации временное сопротивление бетона сжатию и начальный модуль упругости бетона увеличивается. При неблагоприятных внешних условиях (низкая влажность воздуха при изготовлении железобетонных элементов, агрессивные воздействия окружающей среды, коррозия бетона различного происхождения и другие воздействия силового и несилового характера) физико-механические показатели бетона снижаются [1]. Как правило, во всех случаях отмечается неравномерное распределение свойств бетона по сечению, интенсивность которого зависит от характера и степени воздействия. Зависимости (4)-(9) не предусматривают возможности учета переменных начальных модулей упругости бетона по нормальному сечению, что при существенных снижениях исходных показателей может привести к переоценке железобетонного элемента по прочности, жесткости и трещиностойкости. При этом выражения для численной оценки жесткостных характеристик являются физически понятными и обладают гибкостью к трансформации математической записи. Если по глубине сечения, нормального к продольной оси элемента, установить закономерности изменения прочностных и деформативных свойств, а в записях формул (4)-(9) заменить Е_b на Е_bi, то можно получить выражения, обеспечивающие возможность расчета железобетонных элементов с дифференцированной оценкой прочностных и деформативных свойств бетона в каждом отдельном элементарном участке сечения.

Бетон поверхностных слоев конструкции, непосредственно контактирующий с окружающей средой, в большей степени подвергается внешнему воздействию и имеет наибольшую степень отклонения физико-механических параметров бетона от проектных (или начальных) значений. Ближе к центру сечения прочностные и деформативные параметры бетона практически одинаковые и существенно не отличаются по величине (рис. 1, б). При разбиении нормального сечения на элементарные участки данную особенность необходимо учитывать для оптимизации процедуры дискретизации. В случае действия изгибающего момента в одной из плоскостей симметрии рассчитываемого сечения разбиение рекомендуется выполнять таким образом, чтобы максимально дифференцировать учет зон сечения с неоднородными прочностными и деформативными свойствами бетона по толщине элемента при минимальном числе участков разбиения. Для поверхностных зон сечения с высоким градиентом изменения исходных параметров бетона выделяемые участки должны иметь минимальную площадь. Ближе к центру сечения допускается увеличивать размеры элементарных участков с незначительным или отсутствующим изменением параметров по их площади (рис. 1, в). В качестве расчетного параметра начального модуля упругости бетона Е_bi в пределах элементарного участка А_bi может быть принято значение на уровне его центра тяжести. С некоторым запасом также возможно задание этой величины по минимальному значению на границе выделяемого участка.

Приобретенная неоднородность деформативных свойств бетона в конечном итоге сказывается на увеличении общих деформаций элемента с одновременным ростом деформаций (и напряжений) отдельных участков сечения. Уменьшение прочностных свойств бетона на поверхности конструкции отражается на перераспределении напряжений и приводит к смещению результирующего усилия вглубь сечения, что влияет на расчетную величину несущей способности.

В целом предложенный алгоритм расчета железобетонного элемента с переменными свойствами бетона и принцип оптимальной дискретизации нормального сечения позволяет учитывать в расчетах конструкций приобретенную при изготовлении и эксплуатации неоднородность на основе нелинейной деформационной модели с сохранением основополагающих предпосылок и допущений.

Литература:

1. Ерышев В. А., Ерышева Е. В., Тошин Д. С. и др. Оценка степени коррозионного поражения эксплуатируемых железобетонных конструкций покрытия // Градостроительство, реконструкция и инженерное обеспечение устойчивого развития городов Поволжья: сб. докладов Всероссийской науч.-практич. конф. / ТГУ. — Тольятти, 2004. С. — 101–104.