В статье рассмотрен подход к выбору оптимального множества параметров контроля качества функционирования дизельной энергетической установки. Подход основан на разработке и анализе математических моделей ее функциональных подсистем, представленных графами в пространстве параметров.
Ключевые слова: техническая диагностика подвижного состава, математическое моделирование, граф-модель.
В процессе эксплуатации дизельных локомотивов возникает задача по определению уровня качества функционирования энергетической установки с целью принятия, при необходимости, обоснованных инженерно-технических решений по его коррекции. Оценка качества функционирования дизельных энергетических установок осуществляется на основе информации о количественных значениях параметров, получаемых в процессе контроля для заданных режимов работы. Параметры при этом должны быть наиболее информативны, а количество их — минимальное.
Решение задачи выбора оптимального количества параметров контроля может быть выполнено посредством соответствующего математического представления исследуемого объекта с последующей обработкой и анализом [1–3]. В качестве математического аппарата моделирования рассмотрим аппарат, базирующийся на понятиях теории графов.
При рассмотрении вопросов математического моделирования сложных энергомеханических объектов, к которым относится дизельная энергетическая установка, с использованием аппарата теории графов большую роль играют принципы, положенные в основу их декомпозиции [1–3]. В настоящей работе дизельная энергетическая установка 1А-5Д49–2 рассматривается как сложная система локомотива 2ТЭ116 [4], которая в свою очередь делится на функционально взаимосвязанные подсистемы: на нулевом уровне декомпозиции (I) выделяется дизельная энергетическая установка; на основном уровне (II) — функциональные системы; на дополнительном уровне (III) — отдельные узлы и функциональные детали систем (рис. 1). Уровни декомпозиции соответствуют уровням контроля или диагностирования.
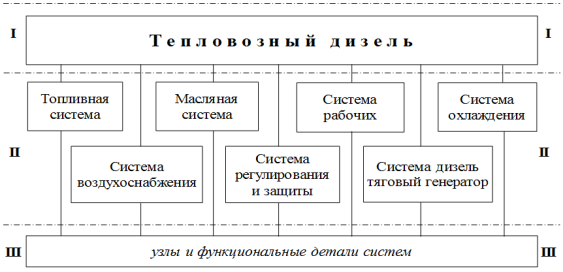
Рис. 1. Функционально взаимосвязанные подсистемы дизельной энергетической установки 1А-5Д49–2
Реализацию предлагаемого подхода рассмотрим на примере топливной системы.
Согласно функциональной схеме топливной системы дизельной энергетической установки 1А-5Д49–2 [4] (рис. 2) топливо из бака (ТБ) через фильтр грубой очистки (ФГО) подается в систему топливоподкачивающим насосом (ТПН). Пройдя через фильтры грубой очистки топливо нагнетается к фильтру тонкой очистки (ФТО) и топливному коллектору (КТ), откуда поступает к топливным насосам дизеля (ТНВД). Топливные насосы дизеля подают топливо по трубопроводам высокого давления к форсункам (Ф).
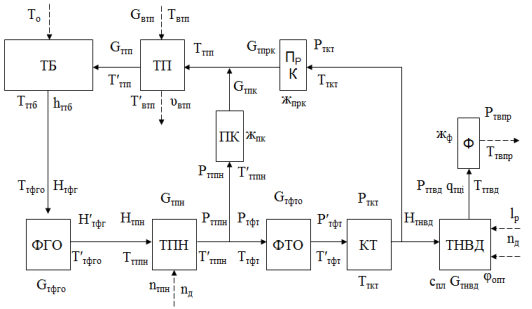
Рис. 2. Функциональная схема топливной системы дизельной энергетической установки 1А-5Д49–2
Для обеспечения давления топлива, необходимого для нормальной работы дизеля, на трубопроводах системы низкого давления установлены предохранительный (ПК) и перепускной клапаны (ПрК). В системе предусмотрен топливоподогреватель (ТП).
Созданию функциональной схемы предшествовал подготовительный этап, включающий в себя анализ сведений о структуре, составе и способе функционирования объекта исследования.
На основе функциональной схемы разработана граф-модель топливной системы в пространстве параметров (рис. 3). Для построения которой функциональные параметры топливной системы представили на модели в виде вершин графа, а причинно-следственные связи между ними, вытекающие из физики функционирования объекта, — ребрами. Ребра проводились независимо от того, известна ли связывающая вершины аналитическая (количественная) зависимость или эта связь носит только качественный характер.
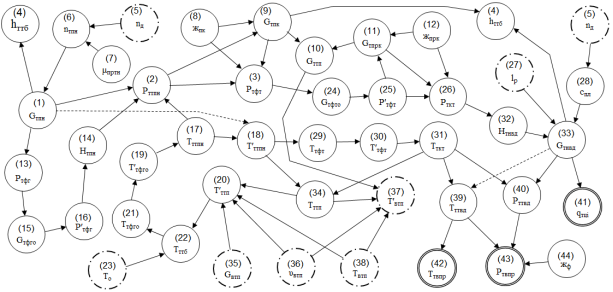
Рис. 3. Граф-модель топливной системы
Разработанная математическая модель функционирования объекта исследования 
задана: множеством функциональных параметров, образующими множество вершин графа Х (полученная граф-модель содержит три типа вершин: тупиковые, имеющие только заходящие ребра; ключевые — только исходящие ребра; смешанные — как исходящие, так и заходящие ребра); конечным множеством ребер U, причем 
; трехместным предикатом 
, 
и 
[2].
Кроме графической реализации разработанной математической модели топливной системы в пространстве параметров, возможна ее интерпретация в матрицу смежности. Понятие матрицы смежности используется на различных этапах обработки граф-моделей, поскольку оно полностью определяют понятие графа [5–7].
Матрица смежности граф-модели 
топливной системы (рис. 4) записывается в виде квадратной матрицы 
размером 
, где n — число вершин граф-модели. Вершины граф-модели в матрице смежности располагаются в произвольном порядке. Элемент матрицы 
стоящий на пересечении i-ой строки и j-го столбца представляет собой коэффициент смежности и принимает следующие значения:
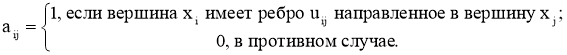(1)
Рис. 4. Матрица смежности граф-модели топливной системы
Обработка граф-модели объекта исследований в пространстве параметров позволяет минимизировать число точек контроля качества его функционирования [1–3].
Математически эта задача решается отысканием минимальных внешне устойчивых подмножеств (МВУП) — Т ориентированного графа, таких, что 
и истинно высказывание [2]:
(2)
где 
— подмножество, образованное отображением вершины х в множестве Х; 
— квантор общности.
Следует отметить, что работа с невзвешенной граф-моделью усложняет выбор единственного МВУП [2, 3, 6].
Для взвешивания граф-модели каждой из ее вершин поставили в соответствие вещественное число 
— вес вершины граф-модели. В качестве 
приняли число голосов, отданных за вершину с учетом веса соответствующего ей параметра [2]:
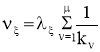(3)
где λξ — вес параметра ξ-й вершины; μ — число скобок в КНФ, в которой находится ξ-я вершина; kν — число вершин в ν-й скобке КНФ, в которой находится ξ-я вершина. КНФ (конъюнктивно нормальная форма) — сложное логическое высказывание, которое для граф-модели рассматриваемой системы запишется следующим образом:
.
После процедуры взвешивания осуществлена оптимизация граф-модели в пространстве параметров, предусматривающая исключение ключевых вершин, так как информация о них может быть получена в тех смешанных и тупиковых вершинах, в которых они отображаются, а также тех смешанных вершин xi cо сравнительно небольшим показателем νξ, которые полностью заменяются более эффективными вершинами хj [1].
Для определения МВУП использовался алгебраический подход [2], представляющий собой процесс составления и анализа упорядоченных матриц смежности граф-моделей.
Упорядочивание множества вершин граф-модели в матрице смежности A производилось присвоением первых номеров в порядке убывания νξ сначала всем тупиковым вершинам. Дальнейшие номера по порядку аналогичным образом присваивались смешанным и ключевым вершинам соответственно. Из сформированной упорядоченной матрицы смежности А* определили матрицу смежности 
размером 
, удовлетворяющую условию (2), где s — число строк соответствующих количеству вершин графа, отброшенных при минимизации; m — число столбцов содержащих вершины вошедшие в МВУП, 
.
В результате получили достаточно близкое к оптимальному решению задачи МВУП, на основе анализа которого сформировали множество параметров контроля качества функционирования топливной системы:
.
В целом, проведенные исследования показали, что используя понятия теории графов и представляя исследуемый объект через структурные связи его составных элементов и взаимовлияние параметров функционирования возможно составление математической модели объекта в виде конечного ориентированного графа. Полученная таким образом математическая модель наглядно представляется в пространстве параметров и может быть интерпретирована в матрицу смежности, что дает возможность ее последующего анализа и обработки с целью выбора оптимального множества параметров контроля.
Литература:
- В. И. Техническое диагностирование локомотивов [Текст] / В. И. Бервинов. — М.: УМК МПС РФ, 1998. — 193 с.
- Осис Я. Я. Диагностирование на граф-моделях: На примерах авиационной и автомобильной техники [Текст] / Я. Я. Осис и др. — М.: Транспорт, 1991. — 244 с.
- Пушкарев И. Ф. Контроль и оценка технического состояния тепловозов [Текст] / И. Ф. Пушкарев, Э. А. Пахомов. — М.: Транспорт, 1985. — 162 с.
- Филонов С. П. Тепловоз 2ТЭ116 [Текст] / С. П. Филонов и др. — М.: Транспорт, 1996. — 334 с.
- Оре О. Теория графов [Текст] / О. Оре. — М.: Наука, 1980. — 336 с.
- Липатов Е. П. Теория графов и ее применение [Текст] / Е. П. Липатов. — М.: Знание, 1986. — 32 с.
- Емеличев В. А. Лекции по теории графов [Текст] / В. А. Емеличев и др. — М.: Наука, 1990. — 383 с.
