Рассматривается ряд важных гидродинамических задач, обсуждаются возможные пути их решения.

Ключевые слова: уравнение Навье-Стокса, Эйлера, Шрёдингера, Бюргерса, Россби, сингулярное множество.

В начале третьего тысячелетия математический институт Клэя поставил перед математическим сообществом 7 важных «классических» математических задач, решение которых не найдено в течение многих лет. Одна из них (гипотеза Пуанкаре) была решена российским математиком Г. Я. Перельманом в 2002 году. В настоящей работе мы коснемся некоторых аспектов другой задачи из этого списка — проблемы решения системы уравнений Навье-Стокса. Поскольку система Навье-Стокса описывает движение жидкости, то мы также будем рассматривать и другие общие задачи гидродинамики, включая газовую динамику и математическую теорию турбулентности.

Классическая система уравнений Навье-Стокса имеет вид

Здесь предполагается, что плотность жидкости постоянна и равна единице, а также что вязкость тоже равна единице. Задача разрешимости этой системы является шестой проблемой в списке великих проблем тысячелетия, сформулированных математическим институтом Клэя. В настоящей работе мы попытаемся представить некоторые методы и подходы, которые хотя и не решают данную проблему, но могут внести существенный вклад в решение смежных задач гидродинамики, которые тоже очень интересны и, возможно, могут быть решены полностью или хотя бы частично.

Мы начнем с задачи исследования сингулярных множеств решений системы Навье-Стокса. Сингулярное множество решения — это множество, на котором решение является неограниченным в том смысле, что в окрестности любой точки дополнения (к сингулярному множеству) решение является ограниченной функцией. Заметим, что из этого определения следует, что сингулярное множество всегда замкнуто. Оказывается, что для решения проблемы Навье-Стокса достаточно показать, что сингулярное множество пусто (см. [5], [8] и ссылки в этих работах). Возникает «попутная» задача: доказать, что это множество «не очень большое». В работе [5] рассматриваются ситуации, при которых возможно показать, что Хаусдофова размерность сингулярного множества решения системы Навье-Стокса не превышает единицу. Более того, одномерная Хаусдорфова мера этого множества равна нулю. Это тесно связано с классической теоремой сильно-слабой единственности, которая заключается в том, что если имеются слабое решение и сильное решение с теми же начальными данными, то они совпадают. В частности, оба являются сильными решениями. Поэтому, если удастся показать наличие решения с пустым сингулярным множеством, то оно будет сильным (классическим), и поэтому любое другое решение совпадет с этим.

Математическая теория турбулентности находится очень близкой и тесной связи с классической теорией системы Навье-Стокса, которая описывает движение жидкости. Возможно, именно феномен турбулентности не позволяет найти положительное решение для классической задачи Навье-Стокса. Что же такое турбулентность в этих задачах? Если говорить очень упрощенно, то согласно закону Колмогорова-Обухова и следствиям из него, турбулентность — это особый закон поведения преобразования Фурье решения системы Навье-Стокса. Первоначально этот закон был экспериментальным (с математической точки зрения — всего лишь гипотезой), причем с некоторыми параметрами, которые тоже устанавливаются экспериментально. В работах [1] и [8] показывается, как он может быть получен, исходя из математических уравнений, и дается оценка параметров. Интересно, что такой подход может быть применен не только к решениям уравнений Навье-Стокса, но и ко многим другим уравнениям математической физики. Например, к уравнениям Шрёдингера [6], Бюргерса [2]. Турбулентность в уравнении Бюргерса называется «Бюргулентностью». Статистический подход к двумерной турбулентности в уравнении Эйлера описывается в [3]. Важную роль в подходах к установлению единственности и регулярности решений уравнений математической физики играют различные априорные оценки [7], [9], [10].

Еще более сложным, чем уравнение Навье-Стокса, является уравнение Больцмана, которое описывает движение газов с учетом взаимодействия между молекулами. Уравнение Больцмана описывает эволюцию плотности распределения вещества в шестимерном фазовом пространстве координаты-скорость и выглядит следующим образом:

Здесь , , , функция имеет смысл плотности в фазовом пространстве. Задав начальную плотность в момент времени и решив задачу Коши, мы будем знать, что будет происходить в момент времени t в каждой точке пространства. В частности, для каждой точки x мы будем знать в какую сторону, с какой скоростью и сколько вещества движется. Квадратичный оператор Q — это оператор взаимодействия молекул Максвелла-Больцмана, который иногда называют больцмановским оператором столкновений:

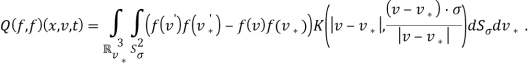
Здесь для краткости опущены аргументы x и t. Штрихованные аргументы скорости, появляющиеся в правой части удовлетворяют соотношениям рассеяния:

и являются функциями от не штрихованных аргументов:

Через обозначается стандартная единичная сфера в трехмерном пространстве. Функция двух переменных K называется ядром больцмановского оператора столкновений. Конкретный ее вид определяется физическими характеристиками вещества и другими предположениями. Например, если , то это означает, что столкновений нет, и вещество может свободно пролетать сквозь себя, без взаимодействий. Интересен случай, когда . Однако, в силу сложности поставленной задачи, приходится делать различные предположения относительно ядра K, которые могут быть не всегда физичными. Наиболее популярные предположения заключаются в том, что ядро К обращается в ноль в окрестности нуля и бесконечности и ограниченно в целом. Заметим, что тогда, как для уравнений Навье-Стокса, фазовое пространство является трехмерным, то для уравнения Больцмана фазовое пространство является шестимерным, поскольку в каждой точке пространства описывается распределение плотности вещества по скоростям (т. е. добавляется еще три координаты). Из-за сложности задачи пока удается решить лишь различные частные случаи. В работе [4] исследуется уравнение Больцмана в предположении, что вещество распределено одинаково по переменным x2 и x3, но произвольно по x1. При этом ограничений на вещество по координатам скорости v1, v2, v3 не накладывается. Поэтому в работе [4] изучается динамика в четырехмерном фазовом пространстве.

Еще одним проявлением феноменов гидро и газовой динамики в больших (планетарных) масштабах, учитывающих влияние силы Корриолиса на движение среды, описывается уравнением Россби, которое в простейшем виде выглядит следующим образом:

В случае, когда x — двумерная координата, т. е. ; функция u является функцией тока поля скоростей среды, т. е. само поле скоростей имеет вид . При этом выписанное уравнение Россби интересно и в многомерном случае (). Функция f описывает различные внешние возмущения. Будем интересоваться решением уравнения Россби в ограниченной области , граница которой  — кусочно-гладкая поверхность. Следуя [15], классическим решением задачи Дирихле для уравнения Россби будем называть функцию , которая удовлетворяет уравнению Россби в классическом смысле (поточечно), начальному условию и граничному условию . Кроме этого, обобщенным решением назовем функцию , если для любой функции и для любого выполнено интегральное соотношение:

Следующее утверждение устанавливает связь между понятиями обобщенного и классического решения.

Теорема 1. Если , то функция будет являться классическим решением тогда и только тогда, когда она будет являться обобщенным.

Доказательство. Если , то для любой функции и для любого момента времени t справедливы равенства:

Здесь для краткости опущены аргументы (x,t) функции u и аргумент x функции h. Точка обозначает обычное (не скалярное) умножение. Таким образом, мы доказали равенство

Вычтя из этого равенства интегральное соотношение, определяющее понятие обобщенного решения, получим эквивалентное равенство:

Таким образом, для функций определение обобщённого решения можно заменить на только что полученное. С другой стороны, в силу произвольности и , последнее равенство эквивалентно исходному уравнению Россби. Для завершения доказательства, остается заметить, что для функций принадлежность пространству равносильно условию . Теорема доказана.

Доказанная теорема играет важную роль в теории уравнения Россби, поскольку она позволяет перенести классическую постановку задачи на «операторный язык». Происходит это потому, что обобщенная постановка задачи для уравнения Россби эквивалента задаче Коши для обыкновенного дифференциального уравнения в банаховом пространстве :

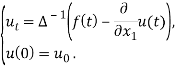
Теорема 2. Функция удовлетворяет указанным выше соотношениям тогда и только тогда, когда она является обобщенным решением уравнения Россби.

Для доказательства теоремы нужно разобраться с обозначениями. Оператор

ставит в соответствие правой части обобщенное решение задачи Дирихле для уравнения Пуассона

Иными словами, тогда и только тогда, когда для любой функции (Q) справедливо интегральное тождество:

Доказательство теоремы 2 заключается в сопоставлении этого тождества и тождества определяющего понятие обобщенного решения.

Оператор является непрерывным в указанных пространствах, что позволяет эффективно реализовывать различные численные и аналитические методы, разработанные для обратного лапласиана, применительно к уравнению Россби, например, метод точечных потенциалов [11–16].

Литература:

1.        Бирюк А. Э. О пространственных производных решений уравнения Навье-Стокса с малой вязкостью // Успехи математических наук. — 2002. — Т. 57. — № 1. — c. 147–148.

2.        Biryuk A. Note on the transformation that reduces the Burgers equation to the heat equation // preprint — 2003. — mp_arc:03–370

3.        Biryuk A. On invariant measures of the 2D Euler equation // Journal of Statistical Physics. — 2006. — Т. 122. — № 4. — c. 597–616.

4.        Biryuk A., Craig W., Panferov V. Strong solutions of the Boltzmann equation in one spatial dimension // Comptes Rendus Mathematique. — 2006. — Т. 342. — № 11. — с. 843–848.

5.        Biryuk A., Craig W., Ibrahim S. Construction of suitable weak solutions of the Navier-Stokes equations // Contemporary Mathematics. — 2007. — V. 429. — c. 1–18.

6.        Biryuk A. Lower bounds for derivatives of solutions for nonlinear Schrödinger equations // Proceedings of the Royal Society of Edinburgh. Section A: Mathematics. — 2009. — V. 139. — № 2. c. 237–251.

7.        Biryuk A. Аn optimal limiting 2D Sobolev inequality // Proceedings of the American Mathematical Society. — 2010. — V. 138. — № 4. — c. 1461–1470.

8.        Biryuk A., Craig W. Bounds on Kolmogorov spectra for the Navier-Stokes equations // Physica D: Nonlinear Phenomena. — 2012. — Т. 241. — № 4. — c. 426–438.

9.        Левицкий Б. Е. Оценки модулей семейств поверхностей, огибающих препятствия. // Сибирский математический журнал. 1990. Т. 31. № 6. С. 104–112.

10.    Левицкий Б. Е., Бирюк А. Э. Cравнение решений нелинейных дифференциальных уравнений с «нагруженными» множествами уровня // Геометрический анализ и его приложения. Материалы II международной конференции, г. Волгоград, 26–30 мая 2014 г. — 2014. — c. 92–94.

11.    Свидлов А. А. Вихревое обтекание острова в канале // Экологический вестник научных центров Черноморского экономического сотрудничества. — 2006. — Спец. выпуск. — c. 141–143.

12.    Свидлов А. А. О начально-краевой задаче для уравнения Россби в ограниченной области // Экологический вестник научных центров Черноморского экономического сотрудничества. — 2008. — № 3. — с. 48–52.

13.    Свидлов А. А. О второй начально-краевой задаче для уравнения Россби в ограниченной области // Экологический вестник научных центров Черноморского экономического сотрудничества. —2009. — № 3. — с. 80–84.

14.    Свидлов А. А., Бирюк А. Э., Дроботенко М. И. Негладкое решение уравнения Россби // Экологический вестник научных центров Черноморского экономического сотрудничества. — 2013. — № 2. — c. 89–94.

15.    Свидлов А. А. Решение линейного уравнения Россби в ограниченной области // Ученые записки Казанского университета. Серия: Физико-математические науки. —2013. —Т. 155. —№ 3. —с. 142–149.

16.    Свидлов А. А., Дроботенко М. И., Бирюк А. Э. Множество единственности потенциала простого слоя // Экологический вестник научных центров Черноморского экономического сотрудничества. — 2015. — № 2. — с. 77–81.